Сила трения
Готовиться с нами - ЛЕГКО!

Сила трения — это сила взаимодействия между соприкасающимися телами, препятствующая перемещению одного тела относительно другого.
Сухое трение
Трение покоя — сила трения, действующая между поверхностями и препятствующая возникновению движения.
Трение скольжения — сила трения, которая действует между проскальзывающими поверхностями. Сила трения скольжения, приложенная к телу со стороны шероховатой поверхности, направлена противоположно скорости движения тела относительно этой поверхности.
Максимальная величина силы трения покоя равна силе трения скольжения.
Абсолютная величина силы трения скольжения прямо пропорциональна силе реакции опоры: \[F_\text{тр}=\mu N\] Коэффициент пропорциональности \(\displaystyle \mu\) называется коэффициентом трения.
Коэффициент трения не зависит от скорости движения тела по шероховатой поверхности.
Коэффициент трения не зависит от площади соприкасающихся поверхностей.
Рыжий Боб тащит прямо и равномерно по горизонтальному полу коробку с котом Тимофеем, прикладывая силу \(F=8\) Н. Найдите массу Тимофея с коробкой, если коэффициент трения между полом и коробкой равен 0,4. Ответ дать в кг.
На рисунке указаны силы, действующие на коробку с котом. 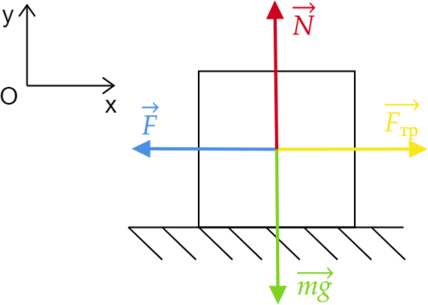 Ускорения у коробки с котом нет, применим первый закон Ньютона.
Ускорения у коробки с котом нет, применим первый закон Ньютона.
Спроецируем силы на ось Oy: \(N=mg\)
Спроецируем силы на ось Ox: \(F_{\text{тр}}=F\)
\(F_{\text{тр}}=\mu N\) – по определению силы трения скольжения.
Т. к. \(N=mg\Rightarrow F_{\text{тр}}=\mu mg\).
Тогда \[F=\mu mg\Rightarrow m=\frac{F}{\mu g}=\frac{8}{0,4\cdot10}=2\text{ кг }\]
На графике представлена зависимость модуля силы трения скольжения от модуля силы нормального давления. Определите коэффициент трения. 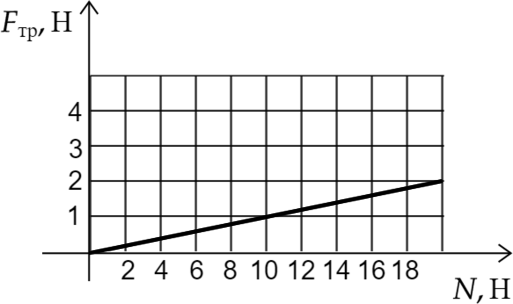
\(F_{\text{тр}}=\mu N\) – по определению силы трения скольжения. Т. е. чтобы найти \(\mu\) нужно найти определенные значения сил нормального давления и трения скольжения.
Для этого необходимо найти удобную точку, где пересекаются вертикаль, горизонталь и сам график. 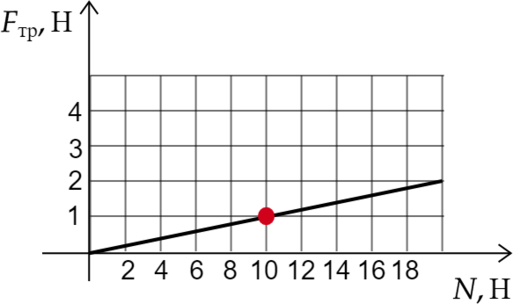
На графике эта удобная точка выделена красным цветом. Т. е. мы поняли, что когда сила трения скольжения равна 1 Н, тогда сила нормального давления равна 10 Н. Теперь можем найти коэффициент трения: \[\mu=\frac{F_{\text{тр}}}{N}=\dfrac{1}{10}=0,1\]
На тело массой 10 кг, которое движется по горизонтальной поверхности, действует сила трения скольжения 40 Н. Чему будет равна сила трения скольжения, если уменьшить массу тела в 4 раза (коэффициент трения не изменится)? (Ответ дайте в Ньютонах.)
Формула для силы трения \(F_{\text{тр}}=\mu N\). В данном случае, так как тело движется горизонтально, то \(N=mg\), поэтому \(F_{\text{тр}}=\mu mg\).
Из этой формулы видно, что при уменьшении массы в 4 раза, сила уменьшится тоже в 4 раза. Следовательно, сила трения станет равной 10 Н.
Санки массой 5 кг скользят по горизонтальной дороге. Сила трения скольжения их полозьев о дорогу 6 Н. Каков коэффициент трения скольжения саночных полозьев о дорогу? Ускорения свободного падения считать равным 10 м/с\(^2\). (Ответ дайте в Ньютонах.)
Сила трения скольжения: \[F_{\text{тр}}=\mu N\]
Так как санки движутся горизонтально, то сила реакции опоры \(N=mg\) \[F_{\text{тр}}=\mu mg\] \[\mu=\frac{F_{\text{тр}}}{mg}=\frac{6}{50}=0,12\]
На тело массой 10 кг действует сила \(F=50\) Н, направленная под углом \(\alpha =30^{\circ}\) к горизонту вверх. Тело лежит на горизонтальной шероховатой поверхности. Коэффициент трения равен \(\mu=0,5\). Чему равна сила трения, действующая на тело? (Ответ дайте в Ньютонах.)
По определению сила трения скольжения равна: \[F_{\text{тр}} = \mu N\] где N – сила реакции опоры.
Рассмотрим силы, действующие на тело: 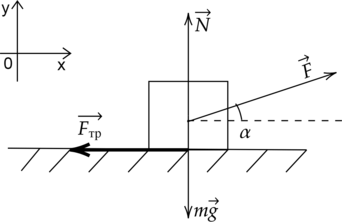
По второму закону Ньютона: \[\vec{F_{\text{тр}}} +\vec{F}+m\vec{g} + \vec{N} = m\vec{a}\] Проекция сил на ось Оy: \[N-mg+ F\sin{\alpha} = 0\Rightarrow N = mg - F\sin{\alpha}\] Отсюда сила трения скольжения равна: \[F_{\text{тр}} = \mu(mg - F\sin{\alpha}) = 0,5\cdot(10\text{ кг}\cdot10\text{ м/с$^2$} - \frac{1}{2}\cdot50\text{ Н}) = 37,5\text{ Н }\] Проекция силы \(\vec{F}\) на ось Ох равна \(F_x=Fcos\alpha=50 \text{ Н}\cdot\dfrac{\sqrt3}{2}=43,3 \text{ Н}\)
Таким образом, \(F_x>F_{\text{тр}}\), значит, тело скользит и сила трения найдена верно.
Какое максимальное ускорение может приобрести автомобиль, чтобы тело, находящееся на горизонтальной поверхности внутри автомобиля, находилось в состоянии покоя относительно транспорта? Коэффициент трения между телом и поверхностью равен 0,5. (Ответ дайте в м/с\(^2\).)
Рассмотрим критический случай, когда ускоение автомобиля приняло максимальное допустимое значение. Так как тело покоится внутри машины, то их ускорение равны: \(a_{\text{т}}=a_{\text{м}} = a\).
По определению сила трения скольжения равна: \[F_{\text{тр}} = \mu N\] где N – сила реакции опоры. 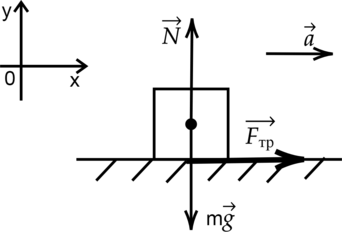
По второму закону Ньютона: \[\vec{F_{\text{тр}}} +m\vec{g} + \vec{N} = m\vec{a}\] Спроецируем силы на оси Оy и Ох: \[Ox: N-mg = 0\Rightarrow N=mg\Rightarrow F_{\text{тр}} = \mu mg\] \[Oy: F_{\text{тр}} = ma \Rightarrow \mu mg = ma\] \[a =\mu g = 0,5\cdot 10\text{ м/с$^2$} = 5\text{ м/с$^2$}\]
Тело массой \(m=10\) кг лежит на наклонной плоскости с углом наклона \(\alpha= 30^{\circ}\) градусов к горизонту. Коэффициент трения равен \(\mu=0,7\). Чему равна сила трения \(F_{\text{тр}}\)? (Ответ дайте в Ньютонах.)
Чтобы ответить на этот вопрос, надо узнать, покоится тело или нет? Для этого рассмотрим момент, когда угол наклона равен критичскому \(\alpha=\alpha_{\text{кр}}\), при котором тело только-только начинает скользить. 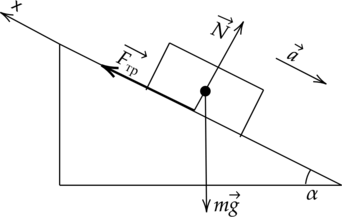
По второму закону Ньютона: \[\vec{F_{\text{тр}}} +m\vec{g} + \vec{N} = m\vec{a}\] Спроецируем уравнение на оси Ох и Оу: \[Ox: F_{\text{тр}}- mg\sin{\alpha_{\text{кр}}}=0 \Rightarrow F_{\text{тр}}= mg\sin{\alpha_{\text{кр}}}\] \[Oy: N-mg\cos{\alpha_{\text{кр}}} = 0\Rightarrow N=mg\cos{\alpha_{\text{кр}}}\] По определению сила трения скольжения равна: \[F_{\text{тр}} = \mu N = \mu mg\cos{\alpha_{\text{кр}}}\] \[mgsin{\alpha_{\text{кр}}} = \mu mg\cos{\alpha_{\text{кр}}}\] Отсюда: \[\mu\cos{\alpha_{\text{кр}}} = \sin{\alpha_{\text{кр}}}\Rightarrow \mu = tg{\alpha_{\text{кр}}}\] Так как \(\alpha_{\text{кр}}\) – угол, при котором тело начинает скользить, а \(tg{\alpha}\) – возастающая функцию на промежутке (0;\(\dfrac{\pi}{2}\)), то для \(\alpha < \alpha_{\text{кр}}\):
если \(\mu < tg{\alpha}\), то тело начнёт скользить;
если \(\mu > tg{\alpha}\), то тело будет покоиться.
Сравним данное значение \(\mu\) с тангенсом наклона: \[0,7 >tg{30^{\circ}} \approx 0,6 \Rightarrow \text{тело покоится}\] Значит, искомая сила – сила трения покоя, которую можно найти из уравнения: \[F_{\text{тр}}= mg\sin{\alpha} = 10\text{ кг}\cdot 10\text{ м/с$^2$}\cdot\frac{1}{2} = 50\text{ H }\]



