Сила трения (страница 2)
Готовиться с нами - ЛЕГКО!

Сила трения — это сила взаимодействия между соприкасающимися телами, препятствующая перемещению одного тела относительно другого.
Сухое трение
Трение покоя — сила трения, действующая между поверхностями и препятствующая возникновению движения.
Трение скольжения — сила трения, которая действует между проскальзывающими поверхностями. Сила трения скольжения, приложенная к телу со стороны шероховатой поверхности, направлена противоположно скорости движения тела относительно этой поверхности.
Максимальная величина силы трения покоя равна силе трения скольжения.
Абсолютная величина силы трения скольжения прямо пропорциональна силе реакции опоры: \[F_\text{тр}=\mu N\] Коэффициент пропорциональности \(\displaystyle \mu\) называется коэффициентом трения.
Коэффициент трения не зависит от скорости движения тела по шероховатой поверхности.
Коэффициент трения не зависит от площади соприкасающихся поверхностей.
Тело массой \(m=10\) кг лежит на наклонной плоскости с углом наклона \(\alpha= 30^{\circ}\) градусов к горизонту. Коэффициент трения равен \(\mu=0,4\). Чему равна сила трения \(F_{\text{тр}}\) (ответ округлите до десятых)? (Ответ дайте в Ньютонах.)
Чтобы ответить на этот вопрос, надо узнать, покоится тело или нет? Для этого рассмотрим момент, когда угол наклона равен критичскому \(\alpha=\alpha_{\text{кр}}\), при котором тело только-только начинает скользить. 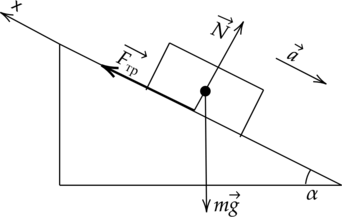 По второму закону Ньютона: \[\vec{F_{\text{тр}}} +m\vec{g} + \vec{N} = m\vec{a}\] Спроецируем уравнение на оси Ох и Оу: \[Ox: F_{\text{тр}}- mg\sin{\alpha_{\text{кр}}}=0 \Rightarrow F_{\text{тр}}= mg\sin{\alpha_{\text{кр}}}\] \[Oy: N-mg\cos{\alpha_{\text{кр}}} = 0\Rightarrow N=mg\cos{\alpha_{\text{кр}}}\] По определению сила трения скольжения равна: \[F_{\text{тр}} = \mu N = \mu mg\cos{\alpha_{\text{кр}}}\] \[mg\sin{\alpha_{\text{кр}}} = \mu mg\cos{\alpha_{\text{кр}}}\] Отсюда: \[\mu\cos{\alpha_{\text{кр}}} = \sin{\alpha_{\text{кр}}}\Rightarrow \mu = tg{\alpha_{\text{кр}}}\] Так как \(\alpha_{\text{кр}}\) – угол, при котором тело начинает скользить, а \(tg{\alpha}\) – возастающая функцию на промежутке (0;\(\dfrac{\pi}{2}\)), то для \(\alpha < \alpha_{\text{кр}}\):
По второму закону Ньютона: \[\vec{F_{\text{тр}}} +m\vec{g} + \vec{N} = m\vec{a}\] Спроецируем уравнение на оси Ох и Оу: \[Ox: F_{\text{тр}}- mg\sin{\alpha_{\text{кр}}}=0 \Rightarrow F_{\text{тр}}= mg\sin{\alpha_{\text{кр}}}\] \[Oy: N-mg\cos{\alpha_{\text{кр}}} = 0\Rightarrow N=mg\cos{\alpha_{\text{кр}}}\] По определению сила трения скольжения равна: \[F_{\text{тр}} = \mu N = \mu mg\cos{\alpha_{\text{кр}}}\] \[mg\sin{\alpha_{\text{кр}}} = \mu mg\cos{\alpha_{\text{кр}}}\] Отсюда: \[\mu\cos{\alpha_{\text{кр}}} = \sin{\alpha_{\text{кр}}}\Rightarrow \mu = tg{\alpha_{\text{кр}}}\] Так как \(\alpha_{\text{кр}}\) – угол, при котором тело начинает скользить, а \(tg{\alpha}\) – возастающая функцию на промежутке (0;\(\dfrac{\pi}{2}\)), то для \(\alpha < \alpha_{\text{кр}}\):
если \(\mu < tg{\alpha}\), то тело начнёт скользить;
если \(\mu > tg{\alpha}\), то тело будет покоиться.
Сравним данное значение \(\mu\) с тангенсом наклона: \[0,4 < tg{30^{\circ}} \approx 0,6 \Rightarrow \text{тело скользит}\] Значит, нужная сила – сила трения скольжения, которую можно найти через силу реакции опоры: \[F_{\text{тр}} = \mu N =\mu mg\cos{\alpha}\] \[F_{\text{тр}} = 0,4\cdot 10\text{ кг}\cdot 10\text{ м/с$^2$}\cdot\frac{\sqrt{3}}{2}\] \[F_{\text{тр}} \approx 34,6\text{ H }\]
Маленькая шайба соскальзывает с горки высотой h и углом наклона к горизонту \(\alpha = 45{^\circ}\) за время \(t=2\) с. Найдите высоту горки, если с наклона \(30^{\circ}\) шайба скользит равномерно (Ответ дайте в метрах и округлите до десятых).
Рассмотрим все силы, действующие на шайбу: 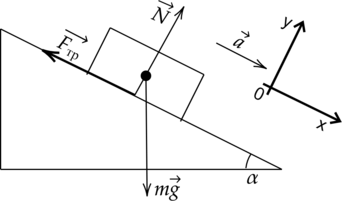
По второму закону Ньютона: \[\vec{F_{\text{тр}}} +m\vec{g} + \vec{N} = m\vec{a}\] Спроецируем уравнение на оси Ох и Оу: \[Ox: mg\sin{\alpha} - F_{\text{тр}}=ma\] \[Oy: N-mg\cos{\alpha} = 0\Rightarrow N=mg\cos{\alpha}\] По определению сила трения скольжения равна: \[F_{\text{тр}} = \mu N = \mu mg\cos{\alpha}\] Значит: \[mg\sin{\alpha} - \mu mg\cos{\alpha}=ma\] \[g(\sin{\alpha} - \mu \cos{\alpha})=a\] Коэффициент трения \(\mu\) можно найти из условия соскальзывания тела. Так как тело только начинает скользить, то ускорения у тела нет, значит, проекция уравнения второго закона Ньютона на ось Ох будет выглядеть так: \[Ox: mg\sin{\alpha_{\text{кр}}} - F_{\text{тр}}=0 \Rightarrow F_{\text{тр}}= mg\sin{\alpha_{\text{кр}}}\] где \(\alpha_{\text{кр}} = 30^{\circ}\) \[F_{\text{тр}} = mg\sin{\alpha_{\text{кр}}} =\mu N = \mu mg\cos{\alpha}\] Отсюда: \[\mu\cos{\alpha_{\text{кр}}} = \sin{\alpha_{\text{кр}}}\Rightarrow \mu = tg{\alpha_{\text{кр}}}\] Подставив это значение в уравнение ускорения, получим: \[a = g(\sin{\alpha} - tg{\alpha_{\text{кр}}}\cdot\cos{\alpha} )\] Запишем уравнение кинематики: \[S = \frac{h}{\sin{\alpha}} = \frac{at^2}{2}\] где S – пройденный путь
Отсюда: \[h = \frac{at^2}{2}\cdot\sin{\alpha} = \frac{g(\sin{\alpha} - tg{\alpha_{\text{кр}}}\cdot\cos{\alpha})\cdot t^2}{2}\cdot\sin{\alpha}\] \[h = \frac{10\text{ м/с$^2$}\left(\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{3}}{3}\cdot\dfrac{\sqrt{2}}{2}\right)\cdot4\text{ c$^2$}}{2} \cdot \frac{\sqrt{2}}{2}\] \[h=10\cdot\left(1 - \frac{\sqrt{3}}{3}\right)\text{ м} \approx 4,2\text{ м }\]
На доску массой \(M=15\) кг, лежащую на гладкой поверхности, положили брусок массой \(m=3\) кг. Какую максимальную горизонтальную силу можно приложить к доске, чтобы брусок оставался в покое? Коэффициент трения между доской и бруском \(\mu = 0,4\). (Ответ дайте в Ньютонах.)
На рисунке изображены силы, приложенные к бруску (левый рисунок) и к доске (правый рисунок): 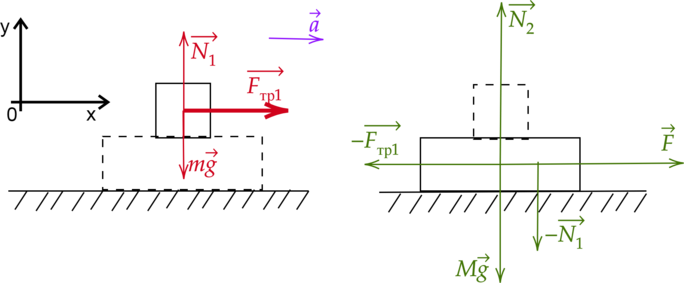
Так как брусок покоится на доске, то ускорения доски и бруска равны \(a_1=a_2=a\). Запишем второй закон Ньютона для бруска: \[\vec{N_1}+\vec{F_{\text{тр}}}+m\vec{g} = m\vec{a}\] Спроецируем на оси Ох и Оу: \[Oy: N_1 - mg = 0\] \[Ox: F_{\text{тр}} = ma\] Рассмотрим критический момент, когда ускорение равно максимальному, тогда брусок ещё не скользит, но сила трения покоя равна силе трения скольжения, тогда: \[F_{\text{тр}} = \mu N = \mu mg\] Подставив это в уравнение проекции второго закона Ньютона на ось Ох, получим: \[\mu mg = ma \Rightarrow a= \mu g\] Теперь запишем второй закон Ньютона для системы “доска + брусок”: \[\vec{N_1}+\vec{F_{\text{тр1}}}+m\vec{g} - \vec{N_1} - \vec{F_{\text{тр1}}}+M\vec{g} + \vec{F} + \vec{N_2}= (m+M)\vec{a}\] \[m\vec{g} + M\vec{g} + \vec{F} +\vec{N_2} = (m+M)\vec{a}\] Спроецировав это на ось Ох, получим: \[F =(m+M)a = (m+M)\mu g\] \[F = (3+15)\text{ кг}\cdot 0,4 \cdot 10\text{ м/с$^2$} = 72\text{ H }\]
На движущееся засчёт горизонтальной силы тело действует сила трения \(F_{\text{тр1}}\). Во сколько раз изменится эта сила, если массу тела уменьшить в два раза?
Рассмотрим силы, действующие на тело 
По втором закону Ньютона: \[\vec{F} + \vec{N} + m\vec{g} +\vec{F}_{\text{тр1}} = m\vec{a}\] где m – масса тела, а – его ускорение.
Спроецируем это уравнение на вертикальную ось: \[N - mg = 0 \Rightarrow N=mg\]
По определению сила трения скольжения равна: \[F_{\text{тр}} = \mu N = \mu mg\] где \(\mu\) – коэффициент трения.
Видно, что сила трения скольжения напрямую зависит от массы тела, значит, если мы уменьшим массу в два раза, то и сила трения скольжения уменьшится в два раза.
На тело массой 10 кг действует горизонтальная сила \(F=30\) Н. Тело лежит на горизонтальной шероховатой поверхности. Коэффициент трения равен \(\mu=0,5\). Чему равна сила трения, действующая на тело? (Ответ дайте в Ньютонах.)
По определению сила трения скольжения равна: \[F_{\text{ск}} = \mu N\] где N – сила реакции опоры.
Рассмотрим силы, действующие на тело: 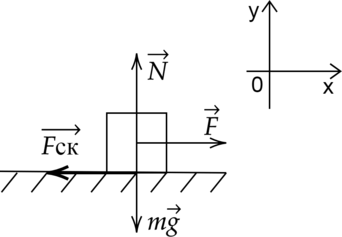
По второму закону Ньютона: \[\vec{F_{\text{ск}}} +\vec{F}+m\vec{g} + \vec{N} = m\vec{a}\] Проекция сил на ось Оy: \[N-mg=0\Rightarrow N=mg\] Отсюда: \[F_{\text{ск}} = \mu mg = 0,5\cdot 10\text{ кг} \cdot 10\text{ м/с$^2$} = 50\text{ H }\] Но тогда получается, что \(F_\text{ск} > F\), и если мы будем тянуть влево, то тело поедет вправо, что физически невозможно. Можно сделать вывод, что данной силы недостаточно, чтобы сдвинуть тело с места, и сила трения равна силе трения покоя, которая равна силе, с которой мы тянем: \[F_{\text{тр}}=F_{\text{покоя}} = F = 30\text{ Н }\]
На графике приведена зависимость модуля силы трения скольжения от модуля силы нормального давления. Каков коэффициент трения?
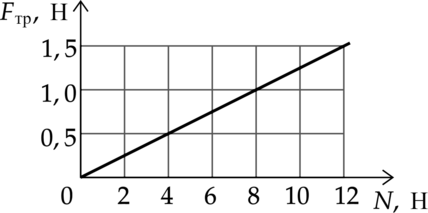
“Демоверсия 2018”
Сила трения: \[F=\mu N\] Откуда коэффициент трени: \[\mu=\dfrac{F}{N}=\dfrac{1,5\text{ Н}}{12\text{ Н}}=0,125\]
По горизонтальному полу по прямой равномерно тянут ящик, приложив к нему горизонтальную силу 35 Н. Коэффициент трения скольжения между полом и ящиком равен 0,25. Чему равна масса ящика
“Демоверсия 2019”
Запишем второй закон Ньютона на оси, с учетом того, что сила трения равна \(F_{\text{ тр}}=\mu N\). \[\begin{cases}
F-F_{\text{ тр}}=0 \Leftrightarrow F=\mu N\\
N=mg\\
\end{cases}\] Из системы \[F=\mu mg \Rightarrow m =\dfrac{F}{\mu g}=\dfrac{35\text{ Н}}{0,25\cdot 10\text{ Н/кг}}=14\text{ кг}\] Где \(F\) – сила, с которой тянут ящик, \(N\) – сила реакции опоры стола, \(\mu\) – коэффициент трения.



