Электрический ток
Готовиться с нами - ЛЕГКО!

Неразветвлённая электрическая цепь постоянного тока состоит из источника тока и подключённого к его выводам внешнего резистора. Как изменятся при уменьшении сопротивления резистора сила тока в цепи и ЭДС источника? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
\[\begin{array}{|c|c|} \hline \text{Сила тока в цепи}&\text{ЭДС источника}\\ \hline &\\ \hline \end{array}\]
“Демоверсия 2017”
ЭДС источник никак не зависит от сопротивления цепи, следовательно, ЭДС истчоника постоянно.
Сила тока в цепи по закону Ома для полной цепи: \[I=\dfrac{\xi}{R+r},\] где \(\xi\) – ЭДС источника, \(R\) – внешнее сопротивление, \(r\) – внутреннее сопротивление.
Если внешнее сопротивление уменьшится, сила тока увеличится.
Неразветвленная электрическая цепь состоит из аккумулятора и резистора. Как изменятся сила тока в цепи и напряжение на клеммах аккумулятора, если в цепь добавить последовательно ещё один резистор?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
\[\begin{array}{|c|c|} \hline \text{Сила тока в цепи}&\text{Напряжение на клеммах аккумулятора}\\ \hline &\\ \hline \end{array}\]
“Досрочная волна 2019 вариант 1”
А) Из закона Ома для полной цепи: \[I=\dfrac{\xi}{r+R_0},\] при последовательном подсоединении общее сопротивление цепи \(R_0\) увеличивается, значит, сила тока уменьшается.
Б) Напряжение на клеммах: \[U=\xi-IR_{0}=\xi-\dfrac{\xi R_0}{R_0+r}=\xi-\dfrac{2\xi R}{2R+r}< \xi- \dfrac{\xi R}{R+r_0}\] Так как сила тока уменьшается, то и напряжение на клеммах уменьшается. Также можно было расписать как \[U=Ir\] Сила тока уменьшается, следовательно, напряжение на клеммах уменьшается
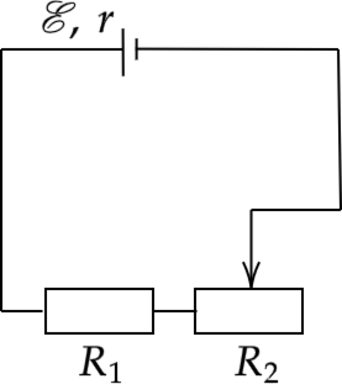
Электрическая цепь состоит из источника тока с ЭДС \(\varepsilon\), резистора \(R_{1}\) и реостата \(R_{2}\). Как изменятся сила тока и тепловая мощность, если уменьшить сопротивление реостата \(R_{2}\)? Внутренним сопротивлением источника тока пренебречь.
1) увеличится
2) уменьшится
3) не изменится
\[\begin{array}{|c|c|}
\hline
\text{ Сила тока }&\text{ Тепловая мощность}\\
\hline
&\\
\hline
\end{array}\]
Сила тока – 1
А) По закону Ома сила тока в цепи равна \[I = \dfrac{\varepsilon}{R_{1} + R_{2}}\] Из этой формулы видно, что при уменьшении сопротивления \(R_{2}\) сила тока в цепи увеличивается.
Тепловая мощность – 1
Б) Тепловая мощность, вырабатываемая электрическим током, равна
\[P = I^{2}\cdot (R_{1} + R_{2}) = \dfrac{\varepsilon^{2}}{(R_{1} + R_{2})^{2}} \cdot (R_{1} + R_{2}) = \dfrac{\varepsilon^{2}}{R_{1} + R_{2}}\]
Так как \(R_{2}\) уменьшается, то из формулы, тепловая мощность увеличивается.
К концам длинного однородного проводника приложено напряжение \(U\). Провод укоротили втрое и приложили к нему прежнее напряжение \(U\). Как изменятся при этом сила тока, мощность тока?
1) увеличится
2) уменьшится
3) не изменится
\[\begin{array}{|c|c|}
\hline
\text{Сила тока }&\text{ Мощность тока }\\
\hline&\\
\hline
\end{array}\]
Сила тока – 1
А)Сопротивление проводника равно
\[R = \dfrac{\rho l}{S},\]
где \(\rho\) – удельное сопротивление материала, \(l\) – длина проводника, \(S\) – площадь проводника При уменьшении длины проводника сопротивление уменьшается.
Сила тока при уменьшении сопротивления увеличивается
\[I = \dfrac{U}{R}.\] Мощность – 1
Б) Мощность тока при уменьшении сопротивления увеличивается \[P = \dfrac{U^{2}}{R}\]
Электрическая цепь состоит из источника тока и телевизора. Источник тока заменили на другой, у которого ЭДС осталось прежней, а внутреннее сопротивление увеличилось. Как изменятся при замене источника тока напряжение на внешнем сопротивлении и сила тока во внешней цепи?
1) увеличится
2) уменьшится
3) не изменится
\[\begin{array}{|c|c|c|}
\hline
\text{ Напряжение на внешнем сопротивлении}&\text{ Сила тока во внешней цепи}\\
\hline
&\\
\hline
\end{array}\]
Напряжение на внешнем сопротивлении – 2
А) Напряжение на внешнем сопротивлении равно
\[U = IR = \dfrac{\varepsilon}{R + r} \cdot R\]
При увеличении внутреннего сопротивления напряжение уменьшается.
Б) Сила тока во внешней цепи – 2
По закону Ома сила тока в цепи равна
\[I = \dfrac{\xi}{R + r},\]
где \(\xi\) – ЭДС источника, \(R\) –— сопротивление телевизора (внешней цепи),\(r\) –— сопротивление источника тока. Как можно заметить при увеличении внутреннего сопротивления источника тока, сила тока в цепи уменьшится.
Плоский конденсатор с воздушным зазором между обкладками подключён к источнику постоянного напряжения. Как изменятся ёмкость конденсатора и разность потенциалов между его обкладками при увеличении площади пластин?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины.
\[\begin{array}{|c|c|}
\hline
\text{ Ёмкость конденсатора }&\text{ Разность потенциалов между}\\
& \text{обкладками конденсатора }\\
\hline
&\\
\hline
\end{array}\]
Электроемкость – 1
А) Электроемкость конденсатора определяется по формуле:
\[C = \dfrac{\varepsilon_{0}\varepsilon S}{d},\]
где \(S\) – площадь конденсатора, \(d\) – расстояние между обкладками, \(\varepsilon\) – диэлектрическая проницаемость диэлектрика, \(\varepsilon_0\) – диэлектрическая постоянная. При увеличении площади пластин ёмкость конденсатора увеличится.
Разность потенциалов – 3
Б) Так как конденсатор подключен к источнику постоянного напряжения, разность потенциалов остается неизменной.
По резистору течёт ток. Резистор заменили на другой, из того же металла и той же площадью поперечного сечения, но имеющий вдвое меньшую длину. Как изменятся при тепловая мощность на резисторе и его сопротивление?
1) увеличится
2) уменьшится
3) не изменится
\[\begin{array}{|c|c|}
\hline
\text{ Тепловая мощность }&\text{ Сопротивление резистора }\\
\hline
&\\
\hline
\end{array}\]
Сопротивление резистора – 2
Сопротивление рассчитывается по формуле:
\[R = \rho \dfrac{l}{S},\]
где \(\rho\) — удельное сопротивление металла, \(l\) — длина, \(S\) — площадь поперечного сечения.
Как видно из формулы, при уменьшении длины проводника, уменьшается сопротивление.
Тепловая мощность – 2
Тепловая мощность, вырабатываемая электрическим током, равна
\[P = I^{2}\cdot R\]
Так как сопротивление \(R\) уменьшается, то тепловая мощность тоже становиться меньше.



