32. Электродинамика. Квантовая физика (расчетная задача) (страница 2)
Готовиться с нами - ЛЕГКО!

Нижняя грань BC прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при основании клина \(\alpha =60^\circ \) Луч света падает из воздуха на клин перпендикулярно грани AC, преломляется и выходит в воздух через другую грань под углом \(\gamma =45^\circ\) к её нормали. Определите показатель преломления материала клина. Сделайте рисунок, поясняющий ход луча в клине. Ответ округлите до десятых
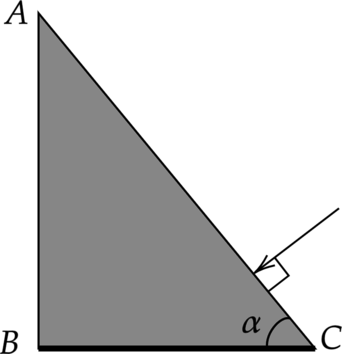
“Основная волна 2020 Вариант 2”
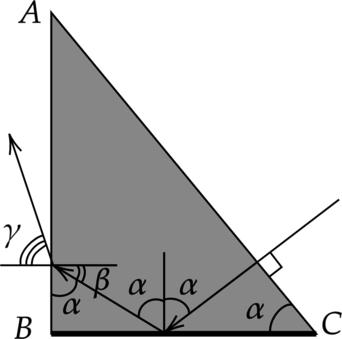 1. Поскольку луч падает на грань AC перпендикулярно, он на ней не преломляется, а, падая на грань BC, согласно закону отражения света отражается под тем же углом Следовательно \[\beta =90-\alpha\] 2. Запишем закон преломления для второго случая. \[n \sin \beta = \sin \gamma \Leftrightarrow n \sin (90-\alpha )=\sin \gamma\] Откуда показатель преломления \[n=\dfrac{\sin \gamma}{\sin \alpha}=\dfrac{\sin 45^\circ}{\cos 60^\circ}=\dfrac{\sqrt{2}}{2\cdot 0,5}=\sqrt{2}\approx 1,4\]
1. Поскольку луч падает на грань AC перпендикулярно, он на ней не преломляется, а, падая на грань BC, согласно закону отражения света отражается под тем же углом Следовательно \[\beta =90-\alpha\] 2. Запишем закон преломления для второго случая. \[n \sin \beta = \sin \gamma \Leftrightarrow n \sin (90-\alpha )=\sin \gamma\] Откуда показатель преломления \[n=\dfrac{\sin \gamma}{\sin \alpha}=\dfrac{\sin 45^\circ}{\cos 60^\circ}=\dfrac{\sqrt{2}}{2\cdot 0,5}=\sqrt{2}\approx 1,4\]
Математический маятник раскачивается с некоторой амплитудой \(A\) в плоскости рисунка. Равновесное положение нити маятника находится на расстоянии \(L= \sqrt{5}\) см от переднего фокуса тонкой положительной линзы. Расстояние между изображениями маятника, лежащими на главной оптической оси линзы, равно \(\Delta\)=2 см, а оптическая сила линзы \(D=5\) дптр. Найти амплитуду колебаний. Ответ дайте в см и округлите до тысячных
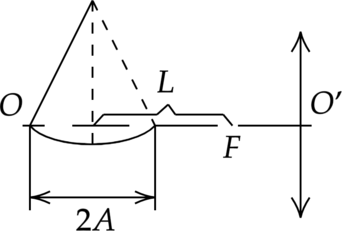
“Основная волна 2020 Вариант 4”
Запишем формулу тонкой линзы для ближайшей точки к линзе колебаний маятника и самой дальней точки. \[D=\dfrac{1}{F+L-A}+\dfrac{1}{f_1}\] \[D=\dfrac{1}{F+L+A}+\dfrac{1}{f_2}\] где \(f_1\) и \(f_2\) – расстояние от линзы до изображений.
а по условию задачи \(f_1-f_2=\Delta\). Из первых двух уравнений выразим \(f_1\) и \(f_2\) и подставим в третье \[\dfrac{1}{f_1}=D-\dfrac{1}{F+L-A} \Rightarrow f_1= \dfrac{F+L-A}{D(F+L-A)-1}\] \[f_2=\dfrac{F+L+A}{D(F+L+A)-1}\] \[\Delta =\dfrac{F+L-A}{D(F+L-A)-1}-\dfrac{F+L+A}{D(F+L+A)-1}=\dfrac{(D(F+L+A)-1)(F+L-A)}{D(F+L-A)-1} -\dfrac{(D(F+L-A)-1)(F+L+A)}{D(F+L+A)-1}\] \[\Delta = \dfrac{2A}{(D(F+L+A)-1)(D(F+L-A)-1)}=\dfrac{2AF^2}{(L-A)(L+A)}=\dfrac{2AF^2}{L^2-A^2}\] Составляем квадратное уравнение \[\Delta A^2 +2AF^2+\Delta L^2=0\] Находим дискриминант \[D=4F^4-4\Delta^2L^2\] отрицательные корни нам не подходят, следовательно, корень данного уравнения \[A=\dfrac{-2F^2+2\sqrt{F^4-\Delta ^2 L^2}}{2\Delta }=\dfrac{20^2\text{ см$^2$}+\sqrt{20^4\text{ см$^4$}+2^2\text{ см$^2$}\cdot 5\text{ см$^2$}}}{2\text{ см}}\approx 0,0125\text{ см}\]
В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности со скоростью \(v = 5\) м/с движется точечный источник света. Расстояние между плоскостями \(d= 15\) см. Центр окружности находится на главной оптической оси линзы. Фокусное расстояние линзы \(F\) = 10 см. Найдите скорость движения изображения точечного источника света. Сделайте пояснительный чертёж, указав ход лучей в линзе.
“Демоверсия 2019”
Сделаем рисунок:
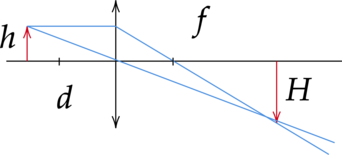
Согласно формуле тонкой линзы, расстояние от предмета до линзы, расстояние от линзы до изображения и фокусное расстояние связаны соотношением \[\dfrac{1}{F}=\dfrac{1}{d}+\dfrac{1}{f}\] Отсюда расстояние от линзы до изображения составляет \[f=\dfrac{Fd}{d-F}\] Линейное увеличение для изображения предмета тонкой линзой равно \[\text{ Г}=\dfrac{H}{h}=\dfrac{f}{d}=\dfrac{F}{d-F},\] где \(H\) – расстояние от главной оптической оси до изображения источника света, \(h\) – расстояние от главной оптической оси до источника света.
Изображение и источник света вращаются относительно главной оптической оси на разных расстояниях, но с одним и тем же периодом. При движении по окружности скорость может быть найдена как \[v=\dfrac{2\pi R}{T}\] Запишем отношение скоростей изображения и источника света и выразим отсюда скорость источника \[\dfrac{v}{v'}=\dfrac{h}{H}=\dfrac{d-F}{F} \Leftrightarrow v= \dfrac{v'(d-F)}{F}\] Подставим числа \[v= \dfrac{(15\text{ см}-10\text{ см}) 10\text{ м/с}}{10\text{ см}}=5\text{ м/с}\]
Тонкая палочка АВ длиной \(l\) = 10 см расположена параллельно главной оптической оси тонкой собирающей линзы на расстоянии \(h\) = 15 см от неё (см. рисунок). Конец А палочки располагается на расстоянии \(a\) = 40 см от линзы. Постройте изображение палочки в линзе и определите его длину \(L\). Фокусное расстояние линзы \(F\) = 20 cм.
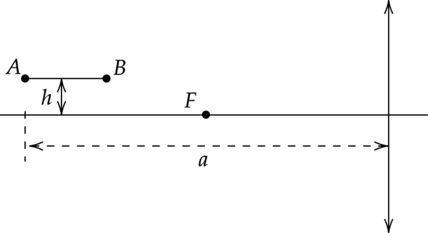
“Демоверсия 2017”
1. Построение изображения \(A'B'\) предмета \(AB\) в линзе показано на рисунке.
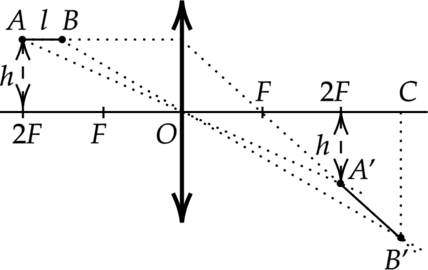
2. Так как точка \(A\) находится на расстоянии \(2F\) от линзы, то её изображение \(A'\) также находится на расстоянии \(2F\) от линзы, и расстояние от точки \(A'\) до главной оптической оси равно \(h\).
3. Длина изображения \(A'B'\) \[L=\sqrt{(OC-2F)^2+(B'C-h)^2}\] 4. Из формулы тонкой линзы \[\dfrac{1}{F}=\dfrac{1}{2F-l}+\dfrac{1}{OC}\] следует \[OC=\dfrac{F(2F-l)}{F-l}=60\text{ см}\] 5. \(\dfrac{B'C}{h}=\dfrac{OC}{2F-l}\), откуда \(B'C= h\dfrac{OC}{2F-l}=30\text{ см}\) 6. Окончательные вычисления \[L=\sqrt{400+225}=25\text{ см}\]
Точечный источник находится на главной оптической оси собирающей линзы с фокусным расстоянием 8 см на расстоянии 6 см от линзы. Линзу начинают смещать со скоростью 3 мм/с в направлении, перпендикулярном оптической оси. С какой скоростью (в мм/с) движется изображение источника?
Формула тонкой линзы для собирающей линзы: \[\frac{1}{F}=\frac{1}{d}+\frac{1}{f}\] где \(F\) – фокусное расстояние,
\(d\) – расстояние от предмета до линзы
\(f\) – растояние от изображения до линзы \[f=\frac{Fd}{F-d}\] \[\Gamma=\frac{f}{d}=\frac{F}{F-d}=\frac{8}{2}=4\]
\(v\) – скорость предмета относительно линзы
\(u\) – скорость изображения источника \[u=v\Gamma=12 \text{ мм/с}\]
Палка, наполовину погружённая в вертикальном положении в воду, отбрасывает на дно бассейна тень длиной \(l = 0, 5\) м. Определите длину выступающей над водой части палки, если глубина воды равна \(h = 3\) м, а угол падения солнечных лучей равен \(\alpha = 30^\circ \) (Показатель преломления воды – 4/3.) Ответ дайте в метрах и округлите до десятых
Построим ход лучей:
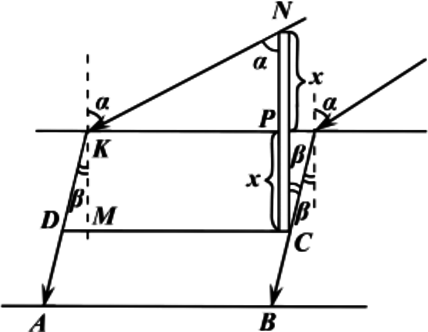
Закон преломления:
\[\sin \alpha=n \sin \beta\] \(n=4 / 3\) (по условию), тогда: \[tg=\frac{\sin \beta}{\cos \beta}=\frac{\sin \beta}{\sqrt{1-\sin ^{2} \beta}}=\frac{\frac{\sin \alpha}{n}}{\sqrt{1-\frac{\sin ^{2} \alpha}{n^{2}}}}=\frac{\sin \alpha}{\sqrt{n^{2}-\sin ^{2} \alpha}}=\frac{1 / 2}{\sqrt{(4 / 3)^{2}-(1 / 2)^{2}}}=\frac{1 / 2}{\sqrt{55 / 36}}=\frac{3}{\sqrt{55}}\] Пусть \(x\) – длина надводной части палки. Палка погружена наполовину, следовательно, длина подводной части – \(x .\) Тогда \[\begin{array}{c} l=|A B|=|C D|=|P K|+|K M| tg \alpha=|P N| tg \alpha+x tg \beta=x tg \alpha+x tg \beta \\ x=\frac{l}{tg \alpha+tg \beta}=\frac{0,5}{\frac{3}{\sqrt{55}}+\frac{1}{\sqrt{3}}} \approx 0,51 \text{ м} \end{array}\]
Бассейн глубиной \(H=4\) м заполнен водой, относительный показатель преломления на границе воздух-вода \(n=4/3\). Какой кажется глубина бассейна наблюдателю, смотрящему в воду вертикально вниз?
Пусть \(h\) – кажущаяся высота.
По закону Снеллиуса \[\dfrac{\sin \beta}{\sin \alpha}= n\] Рассмотрим ход лучей

Тогда \[h=\dfrac{tg \alpha}{tg \beta} H\] Так как углы малые: \[h\approx \dfrac{\sin \alpha}{\sin \beta} H \approx \dfrac{H}{n}=\dfrac{4\text{ м}}{4/3}\approx 3 \text{ м}\]



