32. Электродинамика. Квантовая физика (расчетная задача) (страница 3)
Готовиться с нами - ЛЕГКО!

Пловец, нырнувший с открытыми глазами, рассматривает из под воды светящийся предмет, находящийся над его головой на высоте 75 см над поверхностью воды. Какова будет видимая высота (в см) предмета над поверхностью воды? Показатель преломления воды 4/3. Углы считать малыми, т. е. \(tg\alpha = sin\alpha\).
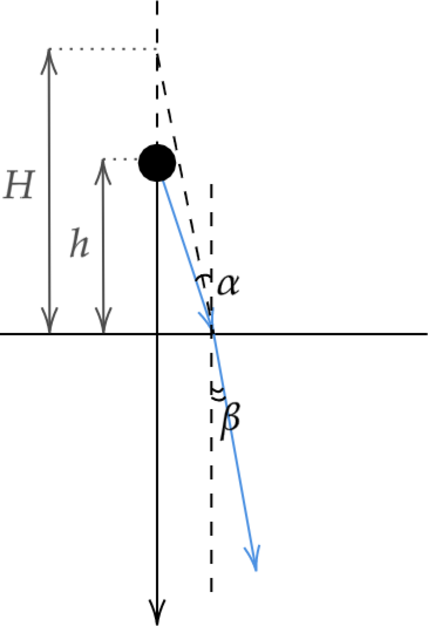
Закон преломления \[\sin\alpha=n\sin\beta,\] где \(n\) – показатель преломления воды, , \(\alpha \) – угол падения, \(\beta\) – угол преломления.
Из прямоугольных треугольников: \[htg\alpha=Htg\beta\] \[h\sin\alpha=H\sin\beta\] \[hn\sin\beta=H\sin\alpha\] \[H=hn=75\cdot4/3=100 \text{ см}\]
Точечный источник света находится в ёмкости с жидкостью и опускается вертикально вниз от поверхности жидкости. При этом на поверхности жидкости возникает пятно, в пределах которого лучи света от источника выходят из жидкости в воздух. Глубина погружения источника (расстояние от поверхности жидкости до источника света), измеренная через равные промежутки времени, а также соответствующий радиус светлого пятна представлены в таблице. Чему равен показатель преломления жидкости? (Ответ дайте с точностью до сотых.) 
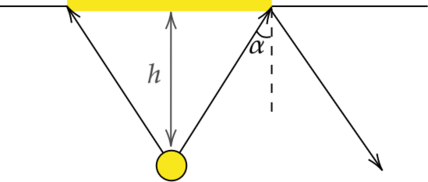
Радиус пятна определяется тем, что не все лучи от источника выходят из воды из-за эффекта полного внутреннего отражения. Рассмотрим предельный случай. \[n\sin\alpha_{\text{кр}}=1\] \[\sin\alpha_{\text{кр}}=\frac{R}{\sqrt{R^2+h^2}}\] \[n=\frac{\sqrt{R^2+h^2}}{R}=\frac{\sqrt{10^2\text{ }+12^2}}{12}=1,30\]
Собирающая линза дает изображение некоторого предмета на экране. Высота изображения 9 см. Оставляя неподвижным экран и предмет, линзу передвинули к экрану и получили второе четкое изображение высотой 4 см. Найдите высоту (в см) предмета.
Формула тонкой линзы для собирающей линзы (1): \[\frac{1}{F}=\frac{1}{d_1}+\frac{1}{f_1}=\frac{d_1+f_1}{d_1f_1}\] где \(F\) – фокусное расстояние,
\(d\) – расстояние от предмета до линзы
\(f\) – растояние от изображения до линзы
Формула тонкой линзы для собирающей линзы (2): \[\frac{1}{F}=\frac{1}{d_2}+\frac{1}{f_2}=\frac{d_2+f_2}{d_2f_2}\] По условию задачи \[d_1+f_1=d_2+f_2\] Значит \(d_1f_1=d_2f_2\) \[d_1f_1f_2+f_1^2f_2=d_2f_1f_2+f_2^2f_1\] \[d_1f_1f_2-d_2f_1f_2=f_2^2f_1-f_1^2f_2\] \[d_2f_2f_2-d_2f_1f_2=f_2^2f_1-f_1^2f_2\] \[d_2f_2(f_2-f_1)=f_2f_1(f_2-f_1)\] \[d_2=f_1,\quad d_1=f_2\]
Увеличение линзы: \[\Gamma_1=\frac{f_1}{d_1}=\frac{d_2}{d_1}=\frac{h_1}{H}\] \[\Gamma_2=\frac{f_2}{d_2}=\frac{d_1}{d_2}=\frac{h_2}{H}\] \[\frac{h_1}{H}=\frac{H}{h_2}\] \[H=\sqrt{h_1h_2}=6 \text{ см}\]
Точечный источник, находящийся на главной оптической оси собирающей линзы на расстоянии от нее, в полтора раза большем фокусного, начинает смещаться со скоростью 4 мм/с перпендикулярно оси. С какой скоростью (в мм/с) движется изображение источника?
Формула тонкой линзы для собирающей линзы: \[\frac{1}{F}=\frac{1}{d}+\frac{1}{f}\] где \(F\) – фокусное расстояние,
\(d\) – расстояние от предмета до линзы
\(f\) – растояние от изображения до линзы \[f=\frac{Fd}{d-F}\] \[\Gamma=\frac{f}{d}=\frac{F}{d-F}=\frac{F}{1,5F-F}=2\] \[H=h\Gamma\]
\(h\) – расстояние от предмета до оси
\(H\) – растояние от изображения до оси
Возьмем производную по времени \[u=v\Gamma=8 \text{ мм/с}\]
Точечный источник находится на главной оптической оси собирающей линзы с фокусным расстоянием 6 см на расстоянии 8 см от линзы. Линзу начинают смещать со скоростью 3 мм/с в направлении, перпендикулярном оптической оси. С какой скоростью (в мм/с) движется изображение источника?
Формула тонкой линзы для собирающей линзы: \[\frac{1}{F}=\frac{1}{d}-\frac{1}{f}\] где \(F\) – фокусное расстояние,
\(d\) – расстояние от предмета до линзы
\(f\) – растояние от изображения до линзы \[f=\frac{Fd}{F-d}\] \[\Gamma=\frac{f}{d}=\frac{F}{F-d}=\frac{8}{2}=4\]
\(v\) – скорость предмета относительно линзы
\(u\) – скорость изображения источника \[u=v\Gamma=12 \text{ мм/с}\]


