Ядерные реакции. Энергия связи
Готовиться с нами - ЛЕГКО!

Используя таблицу масс атомных ядер, вычислите энергию, освобождающуюся при синтезе 1 кг гелия из изотопов водорода — дейтерия и трития: \[^2_1H+^3_1H\rightarrow ^4_2He+^1_0n\]
Ответ дайте разделив его на \(10^{14}\) 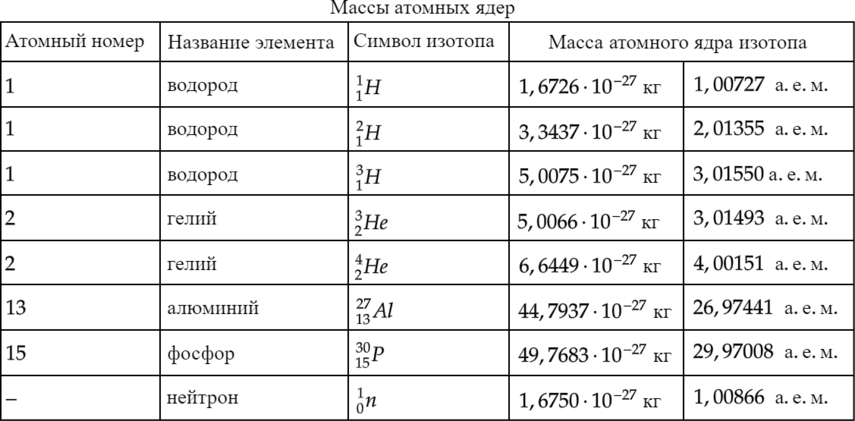
Выход \(\Delta E\) ядерной реакции синтеза ядер гелия из ядер дейтерия и трития вычислим по формуле деффекта массы: \[\Delta E=\Delta mc^2\] \[\Delta m=m_{_1^2H}+m_{_1^3H}-m_{_1^4H}-m_n\]
Найдем деффект массы \(\Delta m\) ядерной реакции: \[\Delta m=2,01355+3,01550-4,00151-1,00866=0,01888\text{ a.e. м}\]
или: \[\Delta m=(3,3437+5,0075-6,6449-1,6750)\cdot 10^{-27}\text{ кг}=3,13\cdot 10^{-29}\text{ кг}\]
Используя переводной коэффициент получим энергетический выход ядерной реакции: \[\Delta E=0,01888 \cdot 931,5\text{ МэВ}\approx=17,6\text{ МэВ}\]
Или Умножим массу на вкадрат скорости света, получим энергетический выход ядерной реакции: \[\Delta E=3,13\cdot 10^{-29}\cdot 9\cdot 10^{16}\text{ Дж}=2,817\cdot 10^{-12}\text{ Дж}\]
Найдем число \(N\) ядер в 1 кг гелия: \[N=\dfrac{m}{m_{He}}=\dfrac{1\text{ кг}}{6,6449\cdot 10^{-27}\text{ кг}}=\approx 1,5\cdot 10^{26}\]
Количество энергии освободившееся при синтезе: \[E=\Delta E\cdot N\approx17,6\cdot 1,6\cdot 10^{-13}\cdot 1,5 \cdot 20^{26}\approx 4,2\cdot 10^{14}\text{ Дж}\]
или \[E=\Delta E\cdot N\approx 2,817\cdot 10^{-12}\cdot 1,5\cdot 20^{26}\approx 4,2\cdot 10^{14}\text{ Дж}\]
При взрыве атомной бомбы освобождается энергия \(8,3\cdot10^{16}\) Дж. Эта энергия получается в основном за счет деления ядер урана 238. При делении одного ядра урана 238 освобождается 200 МэВ, масса ядра равна примерно 238 а. е. м. Вычислите массу ядер урана, испытавших деление при взрыве, и суммарный дефект массы.
Масса \(m\) ядер урана, испытавших деление при взрыве: \[m=Nm_0\]
Число \(N\) ядер равно: \[N=\dfrac{E}{\Delta E}\]
Тогда значение массы: \[m=Nm_0=\dfrac{E\cdot M_0}{\Delta E}=\] \[=\dfrac{8,3\cdot10^{16} \cdot 238 \cdot 1,66 \cdot 10^{-27}}{200\cdot 1,6 \cdot 10^{-13} }\approx 10^3\text{ кг}\]
Найдем деффект массы \(\Delta m\) ядерной реакции: \[\Delta E=\Delta mc^2\]
выразим \(\Delta m\): \[\Delta m=\dfrac{E}{c^2}\] \[\Delta m=\dfrac{8,3\cdot 10^{16}}{9\cdot 10^{16}}\approx 0,92\text{ кг}\]
Находящееся в однородном магнитном поле с индукцией \(B = 5\) Тл ядро покоящегося нейтрального атома испытывает \(\alpha\)-распад, в результате которого рождается ион нового элемента массой \(M = 50\) а.е.м. Его траектория лежит в плоскости, перпендикулярной направлению магнитного поля, и представляет собой дугу окружности радиуса \(R = 5\) см. Найти выделившуюся при \(\alpha\)-распаде энергию \(\Delta E\), считая, что она целиком переходит в кинетическую энергию продуктов реакции. Ответ дайте, разделив его на \(10^(-13)\).
Поскольку исходный атом неподвижен и выделившаяся при реакции энергия \(\Delta E\) целиком переходит в кинетическую энергию продуктов реакции, то из законов сохранения импульса и энергии следуют равенства \[m\upsilon=MV,\] \[\dfrac{m\upsilon^2}{2}+\dfrac{MV^2}{2}=\Delta E,\]
Где \(\upsilon\) и \(V\)–скорости \(\alpha\)–частицы и иона после распада.
Исключая из этих равенств \(\upsilon\), получаем, что \[\Delta E=\dfrac{M(M+m)}{2m}\cdot V^2.\]
Из закона сохранения заряда следует, что модуль заряда иона равен заряду \(\alpha\)–частицы. По второму закону Ньютона уранвение движения иона с магнитном поле под действием силы Лоренца имеет вид \[\dfrac{MV^2}{R}=qVB\]
Подставляя \(V=\dfrac{qBR}{M}\) в найденное выражение для \(\Delta E\), получаем \[\Delta E=\dfrac{(qBR)^2(M+m)}{2Mm}\approx 5,2\cdot 10^{-13}\text{ Дж}\]
При радиоактивном распаде ядра \(^{226}_{88}Ra\) вылетает \(\alpha\)-частица. Известно, что в образце радия массой 1 мг каждую секунду распадаются \(3,7 \cdot 10^7\) ядер. \(\alpha\)-частицы вылетающие из этого образца за 2 часа, имеют суммарную энергию 205 мДж. Какую энергию имеет каждая \(\alpha\)-частица? Ответ приведите в кэВ с точностью \(\pm100\)кэВ.
Пусть \(E_0\) – энергия одной \(\alpha\)-частицы, \(N\) – число распадов ядер в секунду, а, значит, и число \(\alpha\)-частиц, вылетающих из образца за одну секунду. Суммарная энергия вылетевших \(\alpha\)-частиц: \[E=E_0 N t\] \[E_0=\frac{E}{Nt}=\frac{205\cdot10^{-3}}{3,7 \cdot 10^7\cdot7200}=0,77 \cdot10^{-12}\text{ Дж}=4800 \text{ кэВ}\]
Пренебрегая кинетическими энергиями и суммарным импульсом бериллия и гелия в ядерной реакции \[^9_4Be+^4_2He\rightarrow ^{12}_6C+_0^1n\] определить кинетические энергии \(E_C\) и \(E_n\) углерода и нейтрона, считая, что вся выделяющаяся в реакции энергия \(\Delta E\) практически равна \(E_C +E_n.\)
В ответ запишите разность между полученными значениями, разделив, на \(10^{-14}\)
В соответсвии с закономи сохранении энергии сумма масс до реакции равна сумме масс после реакции плюс дефект массы \(\Delta m\), связанный с выделяющейся или поглощающейся энергией \(\Delta E\) соотношением \[\Delta E=|\Delta m|\cdot c^2\]
Используя данные таблицы, получим: \[\Delta m=m_{Be}+m_{\alpha}-m_{C}-m_{n}=9,01219+4,00260-12,00000-1,00867=0,00612\text{ а.е. м.},\]
где \(m_{\alpha}\)– масса образовавшейся \(\alpha\)–частицы (ядра \(_2^4He\)). Поскольку \(\delta m\)>0, в реакции происходит выделение энергии \[\Delta E=(m_{Be}+m_{\alpha}-m_{C}-m_{n})\cdot c^2.\]
По условию суммарный импульс бериллия и гелия равен нулю, поэтому суммарный импульс углерода и нейтрона \[p_C+p_n=0.\]
Суммарная кинетическая энергия бериллия и гелия по условию также равна нулю, следовательно, вся выделяющаяся в реакции энергия \[\Delta E=E_C+E_n,\] где \[E_C=p^2_C/2m_C\text{ и } E_n=p^2_n/2m_n\]
–кинетическая энергия углерода и нейтрона
Отсюда получаем : \[E_n=\dfrac{m_n(m_{Be}+m_{\alpha}-m_{C}-m_{n})\cdot c^2}{m_C+m_n}=\dfrac{1,00867\cdot 0,00612}{12,00000+1,00867}\cdot 1,66\cdot 10^{-27}\cdot(3\cdot10^8)^2\approx7\cdot 10^{-14}\text{ Дж}\] \[E_C=\dfrac{m_c(m_{Be}+m_{\alpha}-m_{C}-m_{n})\cdot c^2}{m_C+m_n}=\dfrac{12\cdot 0,00612}{12,00000+1,00867}\cdot 1,66\cdot 10^{-27}\cdot(3\cdot10^8)^2\approx 8,4\cdot 10^{-13} \text{ Дж}\] \[84-7=77\]


