Электрический ток. Закон Ома (страница 2)
Готовиться с нами - ЛЕГКО!

В схеме, показанной на рисунке, резисторы имеют сопротивления \(R_1 = 1\) Ом, \(R_2 = 2\) Ом. Определить внутреннее сопротивление батареи \(r\) , если известно, что при разомкнутом ключе К через резистор \(R_1\) течет ток \(I_1 = 2,8\) А, а при замкнутом ключе К через резистор \(R_2\) течет ток \(I_2 = 1\) А. Ответ дайте в Ом. 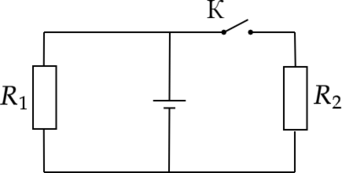
Закон Ома для полной цепи (при разомкнутом ключе): \[I_1=\frac{\xi}{R_1+r}\] \(I\) – сила тока, \(\xi\) – ЭДС источника, \(R\) – внешнее сопротивление, \(r\) – внутреннее сопротивление. При замкнутом ключе \(R_1\) и \(R_2\) подключены параллельно, их общее сопротивление: \[R_{12}=\frac{R_1R_2}{R_1+R_2}=\frac{2}{3} \text{ Ом}\] Напряжение на втором резисторе: \[U_2=I_2R_2=2 \text{ В}\] Напряжение на втором резисторе: \[U_1=U_2=2 \text{ В}\] Ток через первый резистор: \[I_3=\frac{U_1}{R_1}=2 \text{ А}\] Следовательно, общий ток в цепи во втором случае: \[I_4=I_2+I_3=3 \text{ А}\]
Закон Ома для полной цепи (при замкнутом ключе): \[I_4=\frac{\xi}{R_{12}+r}\] \[I_1(R_1+r)=I_4(R_{12}+r)\] \[r=\frac{I_1R_1-I_4R_{12}}{I_4-I_1}=\frac{2,8\text{ А}\cdot1\text{ Ом}-2\text{ В}}{3\text{ А}-2,8\text{ А}}=4 \text{ Ом}\]
В лаборатории имеется однородный медный цилиндрический проводник длиной \(l=10\) м, в опыте к нему приложили разность потенциалов 20 В. Каким будет изменение температуры проводника через 15с? Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь. (Удельное сопротивление меди \(1,7\cdot 10^{-8}\) Ом\(\cdot\)м), ответ дайте в градусах Цельсия.
По закону Джоуля –Ленца не проводнике будет выделяться тепло:
\(Q=\dfrac{U^2 \cdot t}{R}, \quad (1)\) где \(U\) – разность потенциалов(напряжение), \(t\) – время, \(R\) – сопротивление проводника, оно находится по формуле: \[R=\dfrac{\rho l}{S}\quad (2)\]
\(\rho\)-Удельное сопротивление меди, \(S\) – площадь сечения проводника
Так как изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь, то все тепло пойдет на нагревание проводника
\[Q=cm\Delta t, (2)\]
\(c\)-удельная теплоемкость меди=385 (Дж/кг\(\cdot\)К), \(m\) – масса проводника, ее мы найдем по формуле:
\(m=\rho_0 V=\rho_0 lS \quad (3)\)
\(V\) – объем, \(\rho_0=8930\) кг/м\(^3\)-плотность меди
приравняем (1) и (3) с учетом (2) и (4)
\[\dfrac{U^2 \cdot t}{\dfrac{\rho l}{S}}=c\rho_0 lS\Delta t\] Выразим изменение температуры \[\Delta t=\dfrac{U^2 \cdot t}{c\rho_0 \rho l^2}\] Найдем изменение температуры \[\Delta t=\dfrac{400\text{ В$^2$}\cdot 15\text{ с}}{385\text{ Дж/(кг$\cdot$К)}\cdot8930\text{ кг/м$^3$}\cdot1,7\cdot 10^{-8}\text{ Ом$\cdot$м}\cdot 100\text{ м$^2$}}=1026,57^\circ C\]
Электрическая цепь состоит из источника тока и реостата. ЭДС источника\(\xi=6\) В его внутреннее сопротивление \(r=3\) Ом. Сопротивление реостата можно изменять в пределах от 1 Ом до 7 Ом. Чему равна максимальная мощность тока, выделяемая на реостате? Ответ дайте в Вт.
Мощность тока находится по формуле: \[P=UI,\] где \(U\) – напряжение, \(I\) – сила тока и она находится по формуле: \[I=\dfrac{\xi}{R+r} \Rightarrow R=\dfrac{\xi}{I}-r\quad (1)\] А напряжение с учетом (1): \[U=IR=\dfrac{\xi}{R+r}R=\xi-Ir\] Подставив в формулу для расчета мощности, получим: \[P(I)=\xi I-I^2r\] Графиком данного уравнения будет парабола, ветви которой направлены вниз, а его корни \(I_1=0\) и \(I_2=\dfrac{\xi}{r}\), значит, в вершине мощность будет максимальна, а координата данной вершины находится по середине его корней \[\dfrac{I_1 +I_2}{2}=\dfrac{0+\dfrac{\xi}{r}}{2}=\dfrac{\xi}{2r}\] Другой способ нахождения вершины параболы \(I_\text{ в}=\dfrac{-b}{2a}=\dfrac{-\xi}{-2r}=\dfrac{\xi}{2r}\)(значит значения реостата должно быть \(2r\), то есть 6, что лежит в его допустимых значениях.) Тогда максимальная мощность равна \[P=\xi\cdot \dfrac{\xi}{2r}-\dfrac{\xi^2}{4r^2}r=\dfrac{\xi^2}{4r}=\dfrac{36\text{ В$^2$}}{12\text{ Ом}}=3\text{ Вт}\]
В цепи, изображенной на рисунке, подключены источника тока без внутреннего сопротивления, резисторы \(R_1\) и \(R_2\) и ключ. При замкнутом ключе на резисторе \(R_1\) выделяется мощность \(P_1=27\) Вт, а при разомкнутом ключе на резисторе \(R_1\) выделяется мощность \(P_2=3\) Вт. Какая мощность выделяется на резисторе \(R_2\) при разомкнутом ключе. Ответ дайте в Вт. 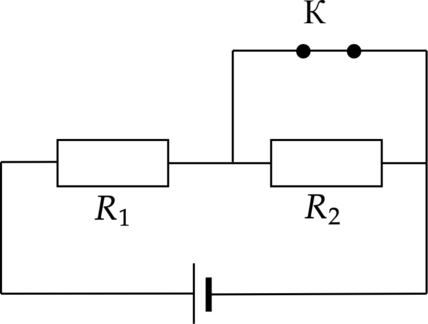
Сила тока при замкнутом ключе равна по закону Ома для полной цепи \[I_1=\dfrac{\xi}{R_1}\] Значит, мощность на первом резисторе при замкнутом ключе равна \[P_1=I_1^2 R_1\dfrac{\xi^2}{R_1}\quad (1)\] где \(\xi\) – ЭДС источника.
При разомкнутом ключе сила тока равна \[I_2=\dfrac{\xi}{R_1+R_2}\] При разомкнутом ключе мощности на первом и втором резисторах равны соответственно \[P_1'=I_2^2R_1=\dfrac{\xi^2R_1}{(R_1+R_2)^2} \quad (2)\] \[P_2'=I_2^2R_2=\dfrac{\xi^2R_2}{(R_1+R_2)^2} \quad (3)\] Поделим (1) на (2), с учетом условия \[\dfrac{(R_1+R_2)^2}{R_1^2}=\dfrac{27\text{ Вт}}{3\text{ Вт}}\] Извлечём квадрат \[\dfrac{R_1+R_2}{R_1}=3 \Rightarrow R_2=2R_1 \quad (4)\] Подставим (4) в (3) с учетом (1) \[P_2'=\dfrac{2\xi^2 R_1 }{9R^2_1}=\dfrac{2}{9}P_1=\dfrac{2}{9}27\text{ Вт}=6\text{ Вт}\]
В цепь включен диод, сопротивление которого в прямом направлении пренебрежительно мало, а в обратном превышает многократно сопротивление резисторов, резисторы \(R_1\) и \(R_2\) и источник тока с ЭДС (см. рисунок). При подключении к точке А положительного полюса, а к точке Б отрицательного полюса источника тока потребляемая мощность равна 14,4 Вт. При изменении полярности потребляемая мощность возрастает до 21,6 Вт. Укажите, как течёт ток через диод и резисторы в обоих случаях, и определите сопротивления резисторов в этой цепи. Ответ выразите в Омах. ЭДС источника 12 В.
Сборник Демидова 2020 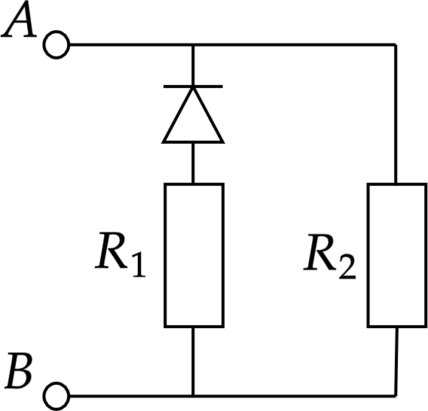
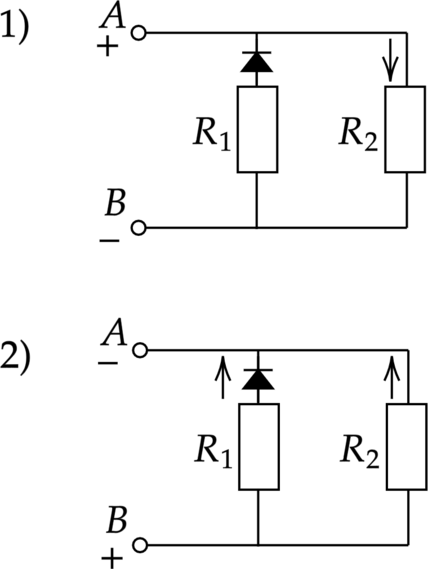 В первом случае ток течет только через резистор \(R_2\), а значит мощность, выделяемая в цепи равна \[P_1=\dfrac{\xi^2}{R_2},\] где \(\xi\) – ЭДС источника.
В первом случае ток течет только через резистор \(R_2\), а значит мощность, выделяемая в цепи равна \[P_1=\dfrac{\xi^2}{R_2},\] где \(\xi\) – ЭДС источника.
Отсюда сопротивление второго резистора \[R_2=\dfrac{\xi^2}{P_1}=\dfrac{(12\text{ В})^2}{14,4\text{ Вт}}=10 \text{ Ом}\] Во втором случае ток будет течь через оба резистора, кроме того, так как резисторы подключены параллельно, то на каждом из них будет напряжение \(\xi\), а мощность, выделяемая в цепи, равна \[P_2=\dfrac{\xi^2}{R_1}+\dfrac{\xi^2}{R_2}=\dfrac{\xi^2}{R_1}+P_1\] Откуда сопротивление второго резистора \[R_2=\dfrac{\xi^2}{P_2-P_1}=\dfrac{(12\text{ В})^2}{21,6\text{ Вт}-14,4\text{ Вт}}=20\text{ Ом}\]
Амперметр с внутренним сопротивлением \(R_1=3\) Ом, подключенный к батарее, показывает силу тока \(I=20\) Ом. Вольтметр с внутренним сопротивлением \(R_2=10 \) Ом, подключенный к батарее, показывает напряжение \(U=100\) В. Найдите силу тока на батарее при коротком замыкании. Ответ дайте в Амперах.
Амперметр, при подключении к батарее, показывает силу тока в цепи: \[I=\dfrac{\xi}{R_1+r}, \quad (1)\] где \(\xi\) и \(r\) – ЭДС и внутреннее сопротивление батареи.
При подключении вольтметра, он будет показывает напряжение на себе \[U=\dfrac{\xi}{R_2+r}R_2 \quad (2)\] Поделим (2) на (1) и выразим внутреннее сопротивление источника \[\dfrac{U}{I}=\dfrac{(R_1+r)R_2}{R_2+r}=5 \Rightarrow 30+10r=50+5r \Rightarrow r=4\text{ Ом}\] Подставим в (1) и найдем ЭДС источника \[\xi=I(R_1+r)=25\text{ А}\cdot (5\text{ Ом}+4\text{ Ом})=225\text{ В}\] Теперь находим силу тока короткого замыкания \[I_\text{ к.з.}=\dfrac{\xi}{r}=\dfrac{225\text{ В}}{4\text{ Ом}}=56,25\text{ А}\]
В цепь, состоящую из источника тока и сопротивления \(R=5\) Ом, подключают вольтметр. В первом случае подключают последовательно сопротивлению, во втором параллельно сопротивлению, при этом в обоих случаях показания вольтметра одинаковы. Каково внутреннее сопротивление вольтметра, если сопротивление источника тока \(r=1\) Ом. Ответ дайте в Омах.
В первом случае вольтметр и резистор подключены последовательно, а вольтметр показывает напряжение на себе, значит, по закону Ома для полной цепи: \[U=\dfrac{\xi}{r+R+R'}R', \quad (1)\] где \(R'\) – сопротивление вольтметра.
Во втором случае вольтметр подключен параллельно резистору, а значит общее сопротивление цепи равно \[R_0=\dfrac{R\cdot R'}{R+R'}\] А напряжение на вольтметре равно напряжению на участке \[U=\dfrac{\xi}{r+R_0}R_0=\dfrac{\xi}{r+\dfrac{R\cdot R'}{R+R'}}\dfrac{R\cdot R'}{R+R'} \quad (2)\] Приравняв (2) и (1), получим \[\dfrac{1}{r+R+R'}=\dfrac{R}{({R+R'})r+R\cdot R'} \Rightarrow (Rr+R'r+R\cdot R'=Rr+R^2+R\cdot R') \Rightarrow R'=\dfrac{R^2}{r}\] Откуда сопротивление вольтметра \[R'=\dfrac{25\text{ Ом$^2$}}{1\text{ Ом}}=25\text{ Ом}\]



