31. Электродинамика (расчетная задача) (страница 2)
Готовиться с нами - ЛЕГКО!

1 Напряженность поля плоского воздушного конденсатора, встроенного в схему (см. рис.), \(E\)= 50В/ см. Расстояние между пластинами конденсатора \(d\) = 0, 5 мм, площадь пластин \(S=\) 100 см\(^2\), сопротивление \(R = 5\) Ом, внутреннее сопротивление батареи \(r\)=1 Ом. Определить ЭДС батареи (В), силу притяжения пластин (нН), заряд пластины (пКл). 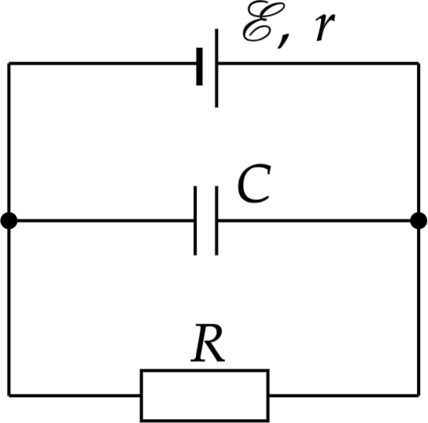
1. Напряжение на конденсаторе равно \[U_c=Ed\] Также это напряжение равно напряжению на резисторе, а значит \[U_c=U_R=IR\] где \(I\)– сила тока в цепи.
Откуда сила тока в цепи \[I=\dfrac{Ed}{R}\] Найдем ЭДС источника по закону Ома для полной цепи \[\varepsilon=Ir+IR= \dfrac{Edr}{R}+Ed= \dfrac{50\text{ В/см} \cdot 0,5\text{ мм}\cdot 0,1\text{ Ом}}{5\text{ Ом}}+50\text{ В/см} \cdot 0,5\text{ мм}=3\text{ В}\] 2. Найдем заряд пластин. Он находится по формуле: \[q=C\cdot U_c\] где \(C\)– ёмкость конденсатора. Напряжение на конденсаторе из первого пункта равно \[U=Ed\] Ёмкость воздушного конденсатора равна \[C=\dfrac{\varepsilon\cdot \varepsilon_0 \cdot S}{d}=\dfrac{\varepsilon_0\cdot S}{d},\] где \(\varepsilon\) – диэлектрическая проницаемость среды (у воздуха она равна 1), \(\varepsilon_0\) – диэлектрическая постоянная. Объединим две предыдущие формулы и получим \[q=\varepsilon_0SE=8,85\cdot 10^{-12}\text{ }\cdot 100\cdot 10^{-4}\text{ м$^2$}\cdot50\cdot 10^{2}\text{ м}=4,425\text{ пКл}\] 3. Сила притяжения пластин конденсатора будет равна производению заряда одной из пластин пластины и напряженности противоположной пластины, а напряженность одной из пластин равна половине напряженности всего конденсатора \[F=q\dfrac{E}{2}=\dfrac{\varepsilon_0E^2S}{2}=\dfrac{8,85\cdot 10^{-12}\text{ }\cdot 100\cdot 10^{-4}\text{ м$^2$}\cdot2500\cdot 10^{4}\text{ м}}{2}=11,0625\text{ нН}\]
Найти напряжения на конденсаторах 1 и 2 в цепи, показанной на рисунке, если известно, что при коротком замыкании сила тока, проходящего через источник, возрастает в \(n=2\) раз, ЭДС источника тока \(\xi=10\).
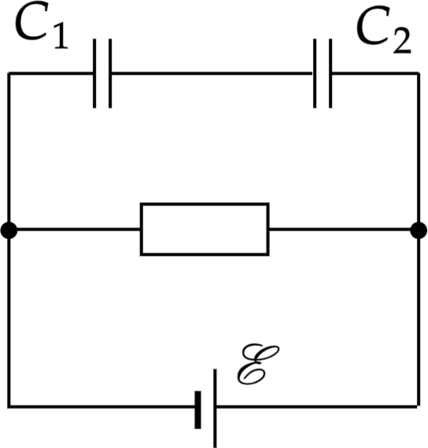
До короткого замыкания сила тока в цепи, по закону ома для полной цепи, равна \[I=\dfrac{\varepsilon}{R+r},\] где \(R\)– сопротивление резистора, \(r\) -– сопротивление источника. При коротком замыкании резистор не будет включен в цепь, а сила тока равна \[I_k=\dfrac{\varepsilon}{r}\] По условию сила тока при коротком замыкании возрастает в \(n\) раз, а значит \[\frac{\frac{\xi}{r}}{\frac{\xi}{R+r}} n \Rightarrow \frac{R}{r}=n-1\] А напряжение на резисторе до короткого замыкания равно \[U_{R}=I R=\frac{\xi R} {R+r}=\frac{\xi(R+r-r)}{R+r}=\xi-\frac{\xi r}{R+r}=\xi-\frac{\xi}{n}=\frac{\xi(n-1)}{n}\] Найдем общую ёмкость конденсаторов, подключенных в цепь \[C=\frac{C_{1} C_{2}}{C_{1}+C_{2}}\] Кроме того, напряжение на блоке конденсаторов будет равно напряжению на резисторах \[U_{C}=U_{R} \Rightarrow \frac{q}{C}=\frac{\xi(n-1)}{n}б\] где \(q\) – заряд на конденсаторах.
Найдем отсюда заряд \[q=\frac{C \xi(n-1)}{n}=\frac{C_{1} C_{2} \xi(n-1)}{\left(C_{1}+C_{2}\right) n}\] Так как конденсаторы подключены последовательно, то заряд на каждом из конденсаторов равен \(q\) Откуда напряжение на конденсаторах \[U_{1}=\frac{q}{C_{1}}=\frac{C_{1} C_{2} \xi(n-1)}{\left(C_{1}+C_{2}\right) n C_{1}}=\frac{C_{2} \xi(n-1)}{\left(C_{1}+C_{2}\right) n}\] \[U_{2}=\frac{q}{C_{2}}=\frac{C_{1} C_{2} \xi(n-1)}{\left(C_{1}+C_{2}\right) n C_{2}}=\frac{C_{1} \xi(n-1)}{\left(C_{1}+C_{2}\right) n}\]
В схему (см. рис.) включены источник тока с ЭДС \(\xi\)= 100 В, сопротивления \(R_1\)= 1 Ом \(R_2\)= 5 Ом и конденсатор ёмкостью \(C=10^{-3}\) Ф. Определить минимальное и максимальное значения силы тока в цепи после замыкания ключа К. В ответ дайте два числа подряд без разделения знаками препинания или пробелами в том порядке, котором спрашивается в условии. 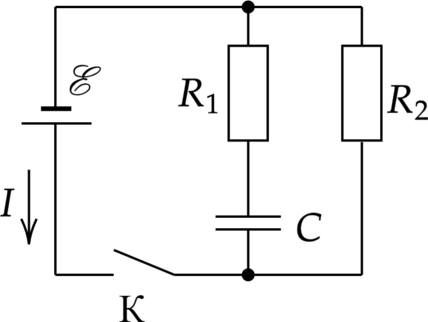
Максимальный ток в цепи будет при полностью разряженном конденсаторе, то есть сразу после замыкания ключа, а минимальный ток будет после полной зарядки конденсатора. Силу тока бyдем находить по закону Oма для полной цепи \[I=\frac{\xi}{R}\] где \( R \) – общее сопротивление цепи.
Общее сопротивление цепи при разряженном конденсаторе равно \[\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}} \Rightarrow R=\frac{R_{1} \cdot R_{2}}{R_{1}+R_{2}}\] Oткуда максимальная сила тока \[I_{\max }=\frac{\xi\left(R_{1}+R_{2}\right)}{R_{1} \cdot R_{2}}=\frac{100 \text{ B}\left(1 \text{ O м}+5 \text{ Oм}\right)}{1 \text{ Oм} \cdot 5 \text{ Oм}}=120 \text{ A}\] При полной зарядке конденсатора, ток через левую ветвь течь не будет, а значит первый резистор будет “выключен” из цепи, а общее сопротивление цепи будет равно \( R_{2}\). Откуда минимальная сила тока равна \[I_{\min }=\frac{\xi}{R_{2}}=\frac{100 \text{ B}}{5 \text{ Oм}}=20 \text{ A}\]
На рисунка показана схема, в которой \(C_1=\) 0,1 мкФ, \(C_2\)= 0, 2 мкФ, \(R_1\)= 1 Ом, \(R_2\) = 8 Ом и \(\xi\)= 3 В. Определить разность потенциалов между точками \(B\) и \(A\). Ответ дайте в В и округлите до сотых
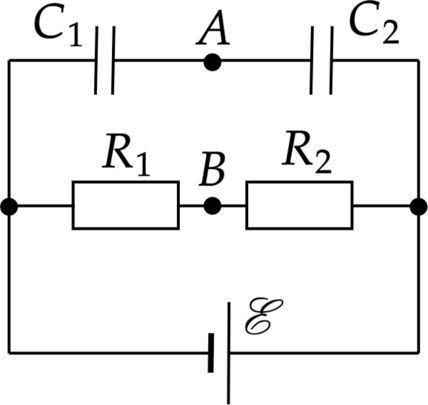
Пусть потенциал в точке \(A \) равен \( \phi_{A}, \) а потентшал в точке\(B-\phi_{B} .\) Тогда заряд на конденсaтope \( C_{1} \) бyдет равен \[q_1=\phi_{A} C_{1}\] А заряд на конденсаторе \(C_2\) равен \[q_1=(\xi-\phi_{A}) C_{2}\] Объединим (1) и (2) и выразим потенциал в точке \(A\) \[\phi_A= \dfrac{\xi C_2}{C_1+C_2}\] Рассмотрим нижнюю ветвь из резисторов \[\phi_B=IR_1 \quad (3)\] \[\phi_B= \xi -IR_2, \quad (4)\] где \(I\) – сила тока в цепи.
Выразим силу тока \[I=\dfrac{\xi}{R_1+R_2}\] Подставим силу тока в (3) \[\phi_B=\dfrac{\xi R_1}{R_1+R_2}\] Найдем разность потенциалов \[\phi_{B}-\phi_{A}=\frac{\xi R_{1}}{R_{1}+R_{2}}-\frac{\xi C_{2}}{C_{1}+C_{2}}=\frac{3 \text{ B} \cdot 1 \text{ Oм}}{1 \text{ Oм}+8 \text{ Oм}}-\frac{3 \text{ B} \cdot 0,2 \text{ мкФ}}{0,1 \text{ мкФ}+0,2\text{ мкФ}}=-\frac{5}{3} \text{ B}\]
Электрическая цепь, схема которой изображена на рисунке, состоит из конденсатора, резистора, источника тока и ключа. Первоначально ключ был разомкнут. Найти ЭДС источника, если известно, что сила тока через источник сразу после замыкания ключа в \(n = 2\) раза больше установившейся силы тока в цепи, а установившееся напряжение на конденсаторе \(U = 1,75\) В. Ответ дайте в В. 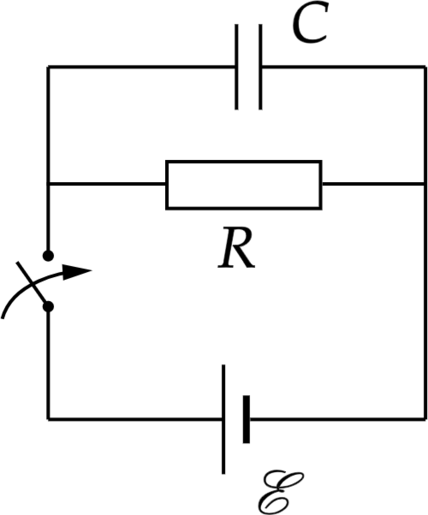
Сразу после замыкания ключа ток через резистор не течет, поэтому ток через источник paset \[I_{1}=\frac{\xi}{r}\] После того, как ток установится, сила тока будет равна \[I_{2}=\frac{\xi}{R+r}\]
так как по условию ток первоначально в \( n \) раз больше, то
\[\frac{\frac{\xi}{r}}{\frac{\xi}{R+r}}=n \Rightarrow \frac{R+r}{r}=n \Rightarrow \frac{R}{r}=n-1\] Taк как конденсатор и резистор подключены параллельно, то напряжение на резисторе равно установившемуся напряжению на конденсаторе и равно \[U=I_{2} R=\frac{\xi R}{R+r}=\frac{\xi(n-1)}{n}\] Откуда ЭДС источника равно \[\xi=\frac{U n}{n-1}=2 U=3,5 \text{ В}\]
Четыре конденсатора подключены к источнику тока, как показано на рисунке. ЭДС источника равно \(\xi=10\) В его внутреннее сопротивление \(r\), ёмкости конденсаторов \(C_1=3C\), \(C_2=2C\), \(C_3=4C\), \(C_4=C=100\) мкФ. Определите энергию на конденсаторе \(C_2\). Ответ дайте в мДж. 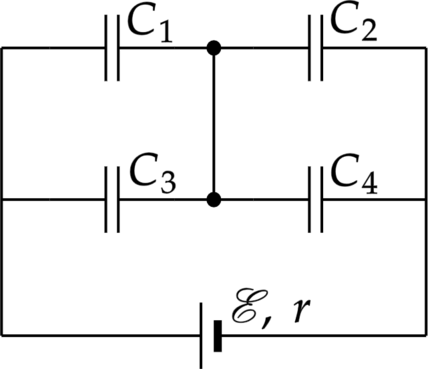
Пусть потенциал между блоком из конденсаторов 1–3 и блоком конденсаторов 2–4 равен \(\phi\), тогда напряжение на блоке 1–3 равно \(U_{13}=\xi-\phi\), а напряжение на блоке 2–4 равно\(U_{24}=\phi-0=\phi\). Найдем емкости блоков конденсаторов \[C_{13}=3C+4C=7C \hspace{10 mm} C_{24}=2C+C=3C\] Так как блок 1–3 и блок 2–4 подключены последовательно, то на них одинаковый заряд \[q_{13}=q_{24} \Rightarrow 7C(\xi-\phi)=3C \phi \Rightarrow \phi=\dfrac{7\xi}{10}\] Так как конденсаторы 2 и 4 подключены параллельно, то напряжение на втором конденсаторе равно напряжению 2–4, а значит энергия второго конденсатора равна \[Q_2=\dfrac{C 49\xi^2}{100\cdot 2}=\dfrac{49C\xi^2}{200}=\dfrac{49 \cdot 200\cdot 10^{-6}\text{ Ф}\cdot 100\text{ В$^2$}}{200}=4,9\text{ мФ}\]
Конденсатор емкостью 2 мкФ присоединен к источнику постоянного тока с ЭДС 3,6 В и внутренним сопротивлением 1 Ом. Сопротивления резисторов \(R_1 =\) 4 Ом, \(R_2\) = 7 Ом, \(R_3\) = 3 Ом. Каков заряд на левой обкладке конденсатора? Ответ дайте в мкКл.
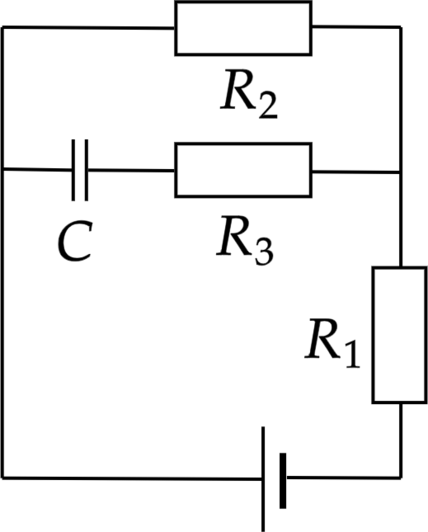
При установившемся токе в цепи ток через конденсатор не будет идти, а значит резистор \(R_3\) не будет включен в цепь.
По закону Ома для полной цепи, ток в цепи равен \[I=\frac{\xi}{r+R_{1}+R_{2}}\] Так как резистор \(R_{2} \) и конденсатор подключены параллельно, то напряжение на конденсаторе напряжению на резисторе \[U_{C}=U_{R_{2}}=I R_{2}=\frac{\xi R_{2}}{r+R_{1}+R_{2}}\] Заряд на конденсаторе и напряжение связаны фopмулой: \[q=C U_{C}\] Найдем заряд на левой обкладке, ом будет равен заряду конденсатора, при этом он будет положительным. \[q=2 \cdot 10^{-6} \Phi \frac{3,6 \text{ В} \cdot 7 \text{ Ом}}{1 \text{ Ом}+4 \text{ Ом}+7 \text{ Ом}}=4,2 \text{ мкКл}\]



