31. Электродинамика (расчетная задача) (страница 3)

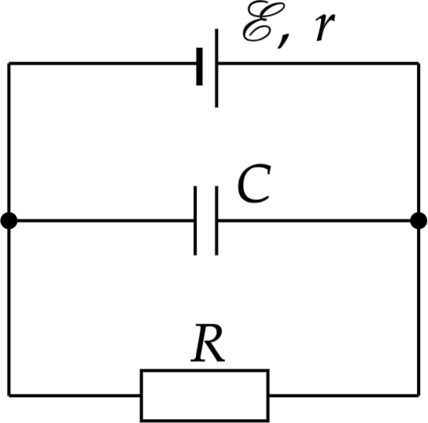
1. Напряжение на конденсаторе равно \[U_c=Ed\] Также это напряжение равно напряжению на резисторе, а значит \[U_c=U_R=IR\] где \(I\)– сила тока в цепи.
Откуда сила тока в цепи \[I=\dfrac{Ed}{R}\] Найдем ЭДС источника по закону Ома для полной цепи \[\varepsilon=Ir+IR= \dfrac{Edr}{R}+Ed= \dfrac{50\text{ В/см} \cdot 0,5\text{ мм}\cdot 0,1\text{ Ом}}{5\text{ Ом}}+50\text{ В/см} \cdot 0,5\text{ мм}=3\text{ В}\] 2. Найдем заряд пластин. Он находится по формуле: \[q=C\cdot U_c\] где \(C\)– ёмкость конденсатора. Напряжение на конденсаторе из первого пункта равно \[U=Ed\] Ёмкость воздушного конденсатора равна \[C=\dfrac{\varepsilon\cdot \varepsilon_0 \cdot S}{d}=\dfrac{\varepsilon_0\cdot S}{d},\] где \(\varepsilon\) – диэлектрическая проницаемость среды (у воздуха она равна 1), \(\varepsilon_0\) – диэлектрическая постоянная. Объединим две предыдущие формулы и получим \[q=\varepsilon_0SE=8,85\cdot 10^{-12}\text{ }\cdot 100\cdot 10^{-4}\text{ м$^2$}\cdot50\cdot 10^{2}\text{ м}=4,425‬\text{ пКл}\] 3. Сила притяжения пластин конденсатора будет равна производению заряда одной из пластин пластины и напряженности противоположной пластины, а напряженность одной из пластин равна половине напряженности всего конденсатора \[F=q\dfrac{E}{2}=\dfrac{\varepsilon_0E^2S}{2}=\dfrac{8,85\cdot 10^{-12}\text{ }\cdot 100\cdot 10^{-4}\text{ м$^2$}\cdot2500\cdot 10^{4}\text{ м}}{2}=11,0625‬\text{ нН}\]

Так как цепь состоит только из конденсатора, то начальное напряжение на конденсаторе равно ЭДС.
Работа внешних сил по изменению энергии в этом случае выглядит следующим образом \[A=W_2-W_1\quad (1)\] где \(W_2\) и \(W_1\) – конечная и начальная энергия в цепи.
Начальная энергия на конденсаторе же равна \[W_1=\dfrac{\varepsilon CU_0^2}{2}\quad (2)\] где \(U_0\) – начальное напряжение на конденсаторе, \(\varepsilon\) – диэлектрическая проницаемость стекла.
Конечная энергия на конденсаторе же равна \[W_2=\dfrac{ CU_1^2}{2}\quad (3)\] где \(U_1\) – конечное напряжение на конденсаторе.
Заряд на конденсаторе находится по формуле: \[q=CU,\] где \(C\) – ёмкость конденсатора, \(U\) – напряжение на конденсаторе.
Запишем закон сохранения заряда для цепи \[\varepsilon CU_0=CU_1 \quad (4) ,\] Объединим (1), (2), (3) \[A=\dfrac{\varepsilon^2 CU_0^2}{2}-\dfrac{\varepsilon CU_0^2}{2}=\dfrac{\varepsilon(\varepsilon-1)CU_0^2}{2}=\dfrac{2(2-1)2\cdot 10^{-6}\text{ Ф}10^6\text{ В$^2$}}{2}=2\text{ Дж}\]

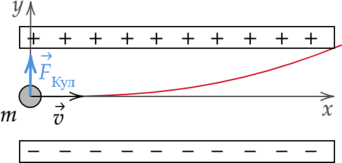
Вдоль оси ОХ – движение равномерное, вдоль оси ОУ – равноускоренное с ускорением: \[a_y=\frac{qE}{m}=\frac{qU}{dm}\] Минимальная скорость будет тогда, когда пылинка при вылете из конденсатора будте находиться на окраине пластины: \[y=\frac{a_yt^2}{2}\] \[\frac{d}{2}=\frac{qUt^2}{2md}\] \[t=\sqrt{\frac{d^2m}{qU}}\] По оси ОХ: \[L=vt\] \[v_{min}=\frac{L}{t}=L\cdot\sqrt{\frac{qU}{d^2m}}=0,1\cdot\sqrt{\frac{1,8\cdot10^{-14}\cdot5000}{0,01^2\cdot10^{-11}}}=30 \text{ м/с}\]

При перемещении шарика из начального положения в конечное на него будут действовать 2 силы: сила тяжести \(mg\) и электрическая сила \(qE\).
По закону сохранения энергии эти две силы будут формировать кинетическую энергию \[E_k=-mgh+ qE S \quad (1)\] где \(h\) – смещение шарика по вертикали, а \(S\) – смещение шарика по горизонтали.
Из геометрической картины имеем, что \(h=l(1- \cos \alpha)\quad (2)\), а \(S=l\sin \alpha\quad (3) \). Распишем изменение кинетической энергии в уравнении (1) и подставим в него (2) и (3) \[\dfrac{mv^2}{2}= -mgl(1-\cos \alpha)+ qEl \sin \alpha\] Отсюда масса шарика \[m=\dfrac{2qEl\sin \alpha}{v^2+2gl(1-\cos \alpha)}=\dfrac{2 \cdot10\cdot 10^{-9}\text{ Кл}\cdot 2000\text{ В/м}\cdot 0,5\text{ м}\cdot 0,5 }{4\text{ м$^2$/с$^2$}+2 \cdot 10\text{ Н/кг}\cdot 0,5 \text{ м}(1-\dfrac{\sqrt{3}}{2})}\approx 2 \text{ мккг}\]

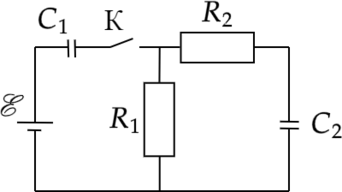
Когда пройдет длительное время, конденсатор будет заряжен до напряжения \(U_1=\xi\), второй конденсатор заряжен не будет (так как он накоротко соединен через резисторы со своими пластинами).
Заряд на первом конденсаторе: \[q_1=C_1U=C_1\xi,\] где \(q_1\) – заряд на первом конденсаторе, тогда работа сторонних сил равна \[A_{\text{ ист}}=q_1\xi=C_1\xi\xi=C_1\xi^2=20\cdot10^{-6}\text{ Ф}\cdot200^2\text{ В$^2$}=0,8 \text{ Дж}\]

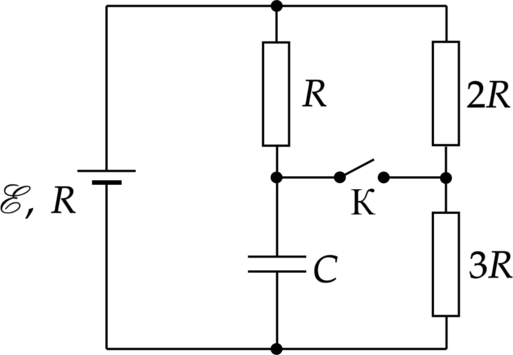
1) 1. Так как резистор \(3R\) и конденсатор подключены паралеллельно, то напряжение на резисторе равно напряжению на конденсаторе и равно общему напряжению на участке \[U_{3R+C}=U_1 \quad (1)\] 2. Так как ток на конденсаторе равен нулю, то сила тока участка “конденсатор + резистор \(3R\)” будет равна только силе тока на резисторе и она в свою очередь равна слие тока участка “резистор \(2R\) + резистор \(R\)” и эта сила тока равна \[I=\dfrac{U_1}{3R}\] 3. Найдем общее сопротивление участка “резистор \(2R\) + резистор \(R\)” \[\dfrac{1}{R}=\dfrac{1}{2R}+\dfrac{1}{R} \Rightarrow R=\dfrac{2R}{3}\] 4. Теперь найдем общее напряжение участка “резистор \(2R\) + резистор \(R\)” \[U_{R+2R}=IR=\dfrac{U_1\cdot 2R}{3R\cdot 3}=\dfrac{2U_1}{9}\quad(2)\] 5. Так как источник тока и участок “резистор \(2R\) + резистор \(R\)” соединены последовательно, то сила тока на источнике и сила тока на участке равна \(I\), значит мы можем найти напряжение на внутреннем сопротивлении источника \[U_\text{ист}=IR=\dfrac{U_1}{3}\quad (3)\] 6. ЭДС источника складывается из напряжени на участках и напряжения на источнике. Сложим (1), (2) и (3). \[U=U_{3R+c}+U_{2R+R}+U_\text{ист}=U_1+\dfrac{2U_1}{9}+\dfrac{U_1}{3}=27\text{ В}+6\text{ В}+9\text{ В}=42\text{ В}\] 2) 1. После установления равновесия в цепи тока черезе резистор \(R\) прекращается, а напряжение на конденсаторе равно напряжению на участке “резистор \(2R\)+ резистор \(3R\)”. 2. Так как ток течет только через участок “резистор \(2R\)+ резистор \(3R\)”, то сила тока в цепи по закону ОМа для полной цепи равна \[I'=\dfrac{\xi}{5R+R}=\dfrac{\xi}{6R}\] 3. Напряжение на участе “резистор \(2R\)+ резистор \(3R\)” равно \[U'=\dfrac{\xi\cdot 5R}{6R}=\dfrac{5\xi}{6}=\dfrac{5 \cdot 42\text{ В}}{6}=35\text{ В}\]

Запишем второй закон Ньютона для пылинки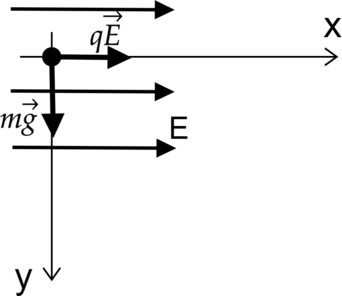

Тогда \[q\vec{E}+m\vec{g}=m\vec{a}\] На ось Ох: \[qE=ma_x\] На ось Оу: \[mg=ma_y\] Тогда тангес угла равен \[tg\alpha=\dfrac{a_x}{a_y}=\dfrac{qE}{mg}\] Выразим напряженность: \[E=\dfrac{tg\alpha mg}{q}\] Так как угол равен 45\(^\circ\), то \(tg\alpha=1\). Найдем напряженность \[E=\dfrac{4\cdot10^{-4}\text{ кг}\cdot 10\text{ м/с$^2$}\cdot 1}{8\cdot10^{-9}\text{ Кл}}=500\text{ кВ/м}\]