Кинематика (страница 2)
Готовиться с нами - ЛЕГКО!

Мячик бросили с балкона, находящегося на высоте \(H\), с начальной скоростью \(v_0\). Определите, как изменятся время и дальность полёта, если высоту увеличить в четыре раза, а начальную скорость шарика уменьшить в 2 раза? Сопротивлением воздуха пренебречь.
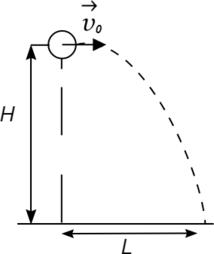
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
\[\begin{array}{|c|c|} \hline \text{Время полёта}&\text{Дальность полёта}\\ \hline & \\ \hline \end{array}\]
1) Введём систему координат с началом в точке О 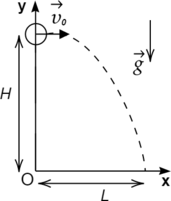
\[\begin{cases} x= x_0+\upsilon_{0x}t+\dfrac {a_xt^2}{2}\\ \\ y= y_0+\upsilon_{0y}t+\dfrac {a_yt^2}{2}\\ \end{cases}\Rightarrow \begin{cases} L= \upsilon_{0}t\\ 0=H -\dfrac {gt^2}{2}\\ \end{cases}\]
Из формулы \(H= \dfrac {gt^2}{2}\) выразим время полёта \(t\), получаем \(t=\sqrt{\dfrac{2H}{g}}\).
Высота \(H\) по условию увеличилась в 4 раза, ускорение \(g=const\), следовательно время полёта \(t\) увеличится в 2 раза.
Ответ под цифрой 1.
2) \(L= \upsilon_{0}t\) – дальность полёта.
Начальная скорость \(\upsilon_{0}\) по условию уменьшилась в 2 раза, а время полёта t увеличилось в 2 раза (из пункта 1) \(\Rightarrow\) дальность полёта не изменится.
Ответ под цифрой 3.
Камень бросили вертикально вверх с поверхности земли с начальной скоростью \(v_0\). Как изменяются потенциальная энергия, модуль скорости камня при движении камня вверх. Сопротивлением воздуха пренебречь.
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
\[\begin{array}{|c|c|} \hline \text{Потенциальная энергия}&\text{Модуль скорости камня}\\ \hline & \\ \hline \end{array}\]
1) \(E_\text{п} = mgh\) – потенциальная энергия камня. Ускорение свободного падения \(g=const\), масса тела по условию не меняется. При движении камня вверх высота, на которой находится камень, увеличивается \(\Rightarrow\) потенциальная энергия увеличивается.
Ответ под цифрой 1.
2) 
Спроецируем уравнение скорости \(\vec{\upsilon}=\vec{\upsilon_0}+\vec{a}t\) на ось \(Oy\) при движении мячика вверх:
\[\upsilon_y=\upsilon_{0}-gt\]
Начальная скорость не меняется по условию, при подъёме мяча время увеличивается \(\Rightarrow\) скорость \(\upsilon_y\) уменьшается.
Ответ под цифрой 2.
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере удаления от земли модуль вертикальной составляющей скорости шарика и его кинетическая энергия.
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
\[\begin{array}{|c|c|} \hline \text{Модуль вертикальной составляющей}&\text{Кинетическая энергия}\\ \text{скорости камня}& \\ \hline & \\ \hline \end{array}\]
1) Спроецируем уравнение скорости \(\vec{\upsilon}=\vec{\upsilon_0}+\vec{a}t\) на ось \(Oy\) при движении шарика вверх: 
\[\upsilon_y=\upsilon_{0y}-gt\]
Т.к. время увеличивается, то \(\upsilon_y\) уменьшается при движении вверх.
Ответ под цифрой 2.
2) Полная механическая энергия \(E\) не изменяется, т.к. сопротивлением воздуха можно пренебречь. \[E= E_\text{п}+E_\text{к}\]
\[E_\text{п} = mgh\]
Высота, на которой находится шарик, увеличивается, следовательно потенциальная энергия увеличивается \(\Rightarrow\) кинетическая энергия уменьшается.
Ответ под цифрой 2.
Шарик, брошенный горизонтально с высоты \(H\) с начальной скоростью \(v_0\), за время \(t\) пролетел в горизонтальном направлении расстояние \(L\) (см. рисунок). Что произойдёт с временем полёта и дальностью полёта, если на этой же установке уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
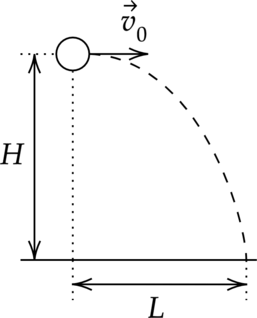
\[\begin{array}{|c|c|} \hline \text{Время полёта} &\text{Дальность полета}\\ \hline &\\ \hline \end{array}\]
“Основная волна 2020 ”
А) Высота полета: \[H=\dfrac{gt^2}{2}\] так как начальная скорость по \(y\) равна 0 и она не изменяется, то время полета \(t\) не изменяется.
Б) Дальность полета: \[S=v_xt\] так как скорость \(v_x\) уменьшилась в 2 раза, то и дальность полета уменьшится в 2 раза.


