Динамика
Готовиться с нами - ЛЕГКО!

C вершины наклонной плоскости из состояния покоя с ускорением скользит тело массой \(m\) (см. рисунок). Как изменятся ускорение и работа силы тяжести, если с той же наклонной плоскости будет скользить тело массой \(\displaystyle \frac{m}{2}\)?

Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
\[\begin{array}{|c|c|}
\hline
\text{Ускорение} & \text{Работа силы тяжести}\\
\hline
& \\
\hline
\end{array}\]
1) Распишем силы, действующие на тело (рис. 1): 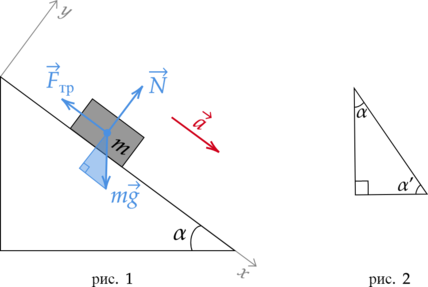
По второму закону Ньютона: \[\vec{F}_{\text{тр}} + \vec{N} + m\vec{g} = m\vec{a}\] Введем оси \(Ox\) и \(Oy\). Спроецируем на них все силы, действующие на тело:
\[\begin{cases} Ox: mg\sin\alpha - F_\text{тр} = ma\\ Oy: N - mg\cos\alpha = 0 \end{cases} \Rightarrow \hspace{3mm} \begin{cases} mg\sin\alpha - \mu N = ma\\ N=mg\cos\alpha \end{cases}\]
\[mg\sin\alpha - \mu mg\cos\alpha = ma\] \[g\sin\alpha - \mu g\cos\alpha = a\] \[a = g(\sin\alpha - \mu\cos\alpha)\] Отсюда получаем, что ускорение не зависит от массы тела \(\Rightarrow\) оно не изменяется.
2) Работа тела находится по формуле: \[A=FS\cos\alpha ',\] где \(F\) — сила, \(S\) — перемещение тела, \(\alpha '\) — угол между вектором перемещения и вектором силы.
В данном случае \(F=F_\text{тяж}=mg\) и \(\alpha ' = 90^\circ - \alpha \Rightarrow \cos\alpha ' = \cos(90^\circ - \alpha) = \sin\alpha\) (рис. 2).
Таким образом, \(A_\text{силы тяжести}=mgS\sin\alpha\)
Значит, работа силы тяжести прямо пропорциональна массе тела.
Массу тела уменьшили \(\Rightarrow\) работа силы тяжести тоже уменьшилась.
C вершины наклонной плоскости из состояния покоя с ускорением скользит тело массой m (см. рисунок). Как изменятся сила трения и скорость тела в конце наклонной плоскости, если с той же наклонной плоскости будет скользить тело массой 3m? 
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
\[\begin{array}{|c|c|c|}
\hline
\text{Сила трения} & \text{Скорость тела в конце наклонной плоскости}\\
\hline
& \\
\hline
\end{array}\]
1) Распишем силы, действующие на тело: 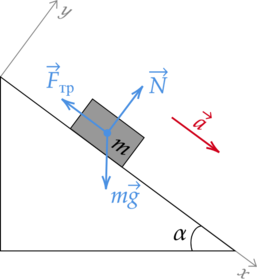
По второму закону Ньютона: \[\vec{F}_{\text{тр}} + \vec{N} + m\vec{g} = m\vec{a}\] Введем оси \(Ox\) и \(Oy\). Спроецируем на них все силы, действующие на тело:
\[\begin{cases} Ox: mg\sin\alpha - F_\text{тр} = ma\\ Oy: N - mg\cos\alpha = 0 \end{cases} \Rightarrow \hspace{3mm} \begin{cases} mg\sin\alpha - \mu N = ma\\ N=mg\cos\alpha \end{cases}\]
\[mg\sin\alpha - \mu mg\cos\alpha = ma\] \[g\sin\alpha - \mu g\cos\alpha = a\] \[a = g(\sin\alpha - \mu\cos\alpha)\] Сила трения равна \(\mu N\), а \(N=mg\cos\alpha\) \(\Rightarrow\) \(F_\text{тр}=\mu mg\cos\alpha\)
Значит, при увеличении массы увеличится и сила трения.
2) \(a = g(\sin\alpha - \mu\cos\alpha)\)
Ускорение никак не зависит от массы тела, поэтому оно не изменится.
Ускорение также равно: \[\displaystyle a=\frac{V-V_0}{t}\] Так как ускорение не изменилось, то и конечная скорость тела в конце наклонной плоскости \(V\) будет такой же.
В результате перехода спутника Земли с одной круговой орбиты на другую его центростремительное ускорение уменьшается. Как изменятся в результате этого перехода расстояние между спутником и Землей и частота его обращения вокруг Земли?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
\[\begin{array}{|c|c|c|}
\hline
\text{Расстояние между спутником и Землей} & \text{Частота обращения вокруг Земли}\\
\hline
& \\
\hline
\end{array}\]
1) Расстояние между спутником и Землей — это и есть радиус орбиты спутника.
На спутник действует сила притяжения Земли: \[F_\text{пр}=G\frac{mM}{R^2},\] где \(G\) — гравитационная постоянная, \(m\) — масса спутника, \(M\) — масса Земли, \(R\) — радиус орбиты. Также по второму закону Ньютона: \[F=ma\] Отсюда следует, что: \[ma=G\frac{mM}{R^2} \Rightarrow a=\frac{GM}{R^2}\] При уменьшении центростремительного ускорения увеличивается радиус орбиты спутника.
2) Частота находится по формуле: \[\nu = \frac{1}{T}\] В свою очередь период обращения равен: \[T=\frac{2\pi R}{V}\] Значит: \[\nu = \frac{V}{2\pi R}\] Нам не известно, как изменяется скорость, но мы знаем, что: \[a=\frac{GM}{R^2}\] \[a_\text{ц.с.}=\frac{V^2}{R}\]
Значит: \[\frac{V^2}{R}=\frac{GM}{R^2} \hspace{3mm} \Rightarrow \hspace{3mm} V^2=\frac{GM}{R}\] При увеличении радиуса орбиты спутника уменьшается его скорость.
\(\Rightarrow\) Частота обращения спутника вокруг Земли уменьшится.
В результате перехода спутника Земли с одной круговой орбиты на другую его центростремительное ускорение уменьшается. Как изменяются в результате этого перехода потенциальная энергия и период обращения спутника?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
\[\begin{array} {| l | l |} \hline \text{Потенциальная энергия} & \text{Период обращения}\\ \hline & \\ \hline \end{array}\]
1) Потенциальная энергия гравитационного взаимодействия равна: \[E_\text{п}= - G \frac{mM}{R},\] где \(G\) — гравитационная постоянная, \(m\) — масса спутника, \(M\) — масса Земли, \(R\) — радиус орбиты.
На спутник действует сила притяжения Земли: \[F_\text{пр}=G\frac{mM}{R^2}\] Также по второму закону Ньютона: \[F=ma\] Отсюда следует, что: \[ma=G\frac{mM}{R^2} \Rightarrow a=\frac{GM}{R^2}\] При уменьшении центростремительного ускорения увеличивается радиус орбиты спутника.
Значит, потенциальная энергия спутника увеличится.
2) Период равен: \[T=\frac{2\pi R}{V}\] \[a=\frac{GM}{R^2}\] Также: \[a_\text{ц.с.}=\frac{V^2}{R}\] Значит: \[\frac{V^2}{R}=\frac{GM}{R^2} \Rightarrow V^2=\frac{GM}{R}\] При увеличении радиуса орбиты спутника уменьшается его скорость, а значит период обращения вокруг Земли будет увеличиваться.
На тело, поступательно движущееся в инерциальной системе отсчёта, действовала постоянная сила \(F\) в течение времени \(\Delta t\). Если время \(\Delta t\) действия силы увеличится, то как изменятся модуль импульса той же силы и модуль ускорения тела?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
\[\begin{array} {| l | l |} \hline \text{Модуль импульса силы} & \text{Модуль ускорения тела}\\ \hline & \\ \hline \end{array}\]
1) Изменение импульса тела равно импульсу силы: \[\Delta p = F\Delta t\] При увеличении времени модуль импульса силы увеличится.
2) Ускорение тела равно: \[a=\frac{F}{m}\] Так как сила и масса тела не изменяются, то ускорение не изменится.
На тело, поступательно движущееся в инерциальной системе отсчёта, действовала постоянная сила \(F\) в течение времени \(\Delta t\). Если действующая на тело сила увеличится, то как изменятся модуль ускорения тела и модуль изменения импульса тела в течение того же промежутка времени \(\Delta t\)?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться. \[\begin{array} {| l | l | }
\hline
\text{Модуль ускорения тела} & \text{Модуль изменения импульса тела}\\
\hline
& \\
\hline
\end{array}\]
1) По 2 закону Ньютона: \[F=ma\] Если сила увеличилась, то модуль ускорения тоже увеличится.
2) Так как ускорение увеличилось, то конечная скорость тоже будет больше, а значит модуль изменения импульса тела \(\Delta p = m\Delta V =F\Delta t\) увеличится.
На шероховатой наклонной плоскости покоится деревянный брусок. Угол наклона плоскости увеличили, но брусок относительно плоскости остался в покое. Как изменились при этом коэффициент трения бруска о плоскость и проекция силы тяжести на ось \(Ox\) (ось параллельна плоскости и направлена к её основанию)?
Для каждой величины определите соответствующий хаарктер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться. \[\begin{array} {| l | l |}
\hline
\text{Коэффициент трения бруска о плоскость} & \text{Проекция силы тяжести на ось } Ox\\
\hline
& \\
\hline
\end{array}\]
1) Коэффициент трения зависит от материала, из которого сделан брусок и наклонная плоскость. Ничего не было изменено, а значит и коэффициент не изменился.
2) Сделаем рисунок, обозначим силы и найдем проекцию силы тяжести на ось \(Ox\): 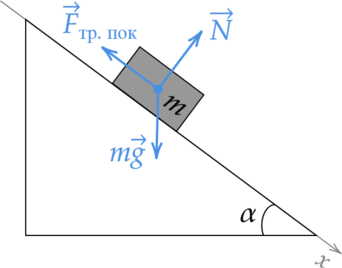
Из рисунка видно, что проекция силы тяжести равна: \[F_x = mg\sin\alpha\] Значит, чем больше будет угол наклона, тем больше будет проекция силы тяжести на ось \(Ox\).



