Гидростатика
Готовиться с нами - ЛЕГКО!

Тело, находящееся в воде или на поверхности, медленно, не останавливаясь, двигают по вертикали.
Установите соответствие между графиками и процессами, которые их описывают.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ГРАФИКИ
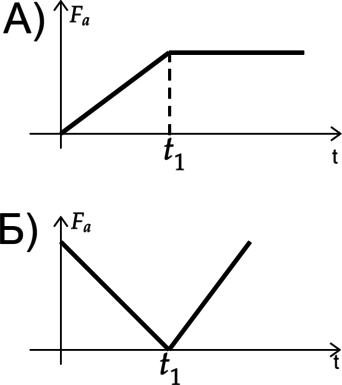
ПРОЦЕССЫ
1) Тело до \(t_1\) опускали вниз, а после \(t_1\) оно полностью погрузилось в воду.
2) Тело до \(t_1\) поднимали, а после оно находилось на поверхности.
3) Тело до \(t_1\) поднимали, а после опускали вниз.
4) Тело всё время находилось на одной глубине погружения.
\[\begin{array}{|c|c|} \hline \text{А}&\text{Б}\\ \hline &\\ \hline \end{array}\]
А) Сила Архимеда находится по формуле \[F_a=\rho g V\] Где \(\rho\) — плотность жидкости, а \(V\) — объем погруженной части тела. Так как сила Архимеда сначала увеличивалась, а затем была постояна, то объем погруженной части тоже увеличивался, а затем был постоянный, а значит тело погружали, пока оно не погрузилось полностью. Ответ — 1
Б) Сила Архимеда сначала уменьшалась, а затем увеличивалась, значит тоже самое происходило и с объемом тела. Ответ — 3
Тело массой \(m\) и объемом \(V\) плавает на поверхности жидкости плотностью \(\rho\) и погружено на \(\dfrac{1}{4}V\).
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
\[\begin{array}{ll} \text{Физические величины}&\text{Формулы}\\ \text{А) Сила тяжести} & \text{1)} \dfrac{1}{4}\rho g V \\ \text{Б) Плотность тела} &\text{2)} \rho g V \\ &\text{3)} \dfrac{1}{4} \rho \\ &\text{4)} \rho \\ \end{array}\]
\[\begin{array}{|c|c|} \hline \text{А}&\text{Б}\\ \hline &\\ \hline \end{array}\]
А) Так как тело плавает, то силу тяжести уравновешивает сила Архимеда \[F_\text{т}=\dfrac{1}{4}\rho g V\]
Ответ – 1
Б) Из пункта А) \[mg= F_\text{т}=\dfrac{1}{4}\rho V\]
Заменим \(m\) на \(\rho_o \cdot V\), где \(\rho_0\) – плотность тела. Получим \[\rho_0 \cdot V= \dfrac{1}{4}\rho V\]
Или \[\rho_o=\dfrac{1}{4}\rho\]
Ответ – 3
Тело сделанное из железа плотностью \(\rho_0\)=7800 кг/м\(^3\) и объемом \(V\)=0,001 м\(^3\) в первом случае погружают в воду, а во втором в ртуть.
Установите соответствие между физическими величинами и их значениями.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
\[\begin{array}{ll} \text{Физические величины}&\text{Значения}\\ \text{А) Сила Архимеда в воде} &1)\ 78\text{ Н} \\ \text{Б) Сила Архимеда в ртути} &2)\ 10 \text{ Н} \\ &3)\ 136 \text{ Н} \\ &4)\ 100 \text{ Н} \\ \end{array}\]
\[\begin{array}{|c|c|} \hline \text{А}&\text{Б}\\ \hline &\\ \hline \end{array}\]
А) Так как плотность железа больше плотности воды, то тело тонет. Значит сила Архимеда находится по формуле \[F_a=\rho_1 g V_\text{т}\]
Где \(\rho_1\) — плотность воды, а \(V_\text{т}\) — объем погруженной части (т.к. тело тонет, то он равен \(V\)).
Найдем силу Архимеда \(F_a=1000\text{ кг/м$^3$} \cdot 10 \text{ м/с$^2$} \cdot 0,001 \text{ м$^3$}= 10\text{ Н} \). Ответ – 2
Б) Так как плотность железа меньше плотности ртути, то тело будет плавать на поверхности и сила Архимеда будет уравновешивать силу тяжести \[F_a=F_\text{т}=mg=\rho_0\cdot V\cdot g\]
Найдем силу Архимеда \(F_a= 7800\text{ кг/м$^3$} \cdot 0,001 \text{ м$^3$} \cdot 10 \text{ м/с}^2= 78 \text{ Н}\). Ответ – 1
Тело объемом \(V\)=0,002 м\(^3\), находящееся в сосуде с водой плотностью \(\rho\)=1000 кг/м\(^3\), двигают по вертикали.
Установите соответствие между графиками и процессами, которые их описывают.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ГРАФИКИ
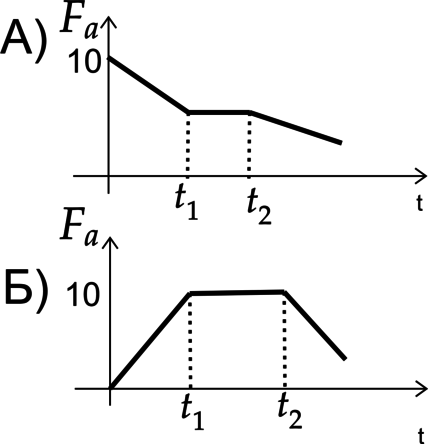
ПРОЦЕССЫ
1) Тело до \(t_1\) погружали в жидкость, от \(t_1\) до \(t_2\) находилось полностью под водой, а от \(t_2\) поднимали вверх.
2) Тело до \(t_1\) поднимали, от \(t_1\) до \(t_2\) было на одной глубине погружений, от \(t_2\) поднимали вверх.
3) Тело до \(t_1\) погружали в жидкость, от \(t_1\) до \(t_2\) было на одной глубине погружений, от \(t_2\) поднимали вверх.
4) Тело всё время находилось на одной глубине погружения.
\[\begin{array}{|c|c|} \hline \text{А}&\text{Б}\\ \hline &\\ \hline \end{array}\]
Найдем максимальную силу Архимеда по формуле \(F_a=\rho \cdot g \cdot V\). \[F_a=1000\text{ кг/м$^3$} \cdot 10 \text{ Н/м} \cdot 0,002 \text{ м$^3$}= 20\text{ Н}\]
А) Заметим, что до \(t_1\) \(F_a\) уменьшалась, от \(t_1\) до \(t_2\) оставалась неизменной, после опять уменьшалась, значит и объем ведет себя также. Ответ – 2
Б) Проанализируем график до \(t_1\) \(F_a\) увеличивалась, от \(t_1\) до \(t_2\) оставалась неизменной, но не доходила до своего максимума, после уменьшалась, найдем подходящий. Ответ 1) не подходит, так как от \(t_1\) до \(t_2\) \(F_a\) не достигла максимума. Ответ – 3
Тело поочередно погружали на полный объем в одну из трех жидкостей с плотностями \(\rho_1\)=\(\rho\), \(\rho_2\)=\(2\rho\) и \(\rho_3\)=\(4\rho\). Представлены два графика. Определите последовательность жидкостей в каждом опыте.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ГРАФИКИ
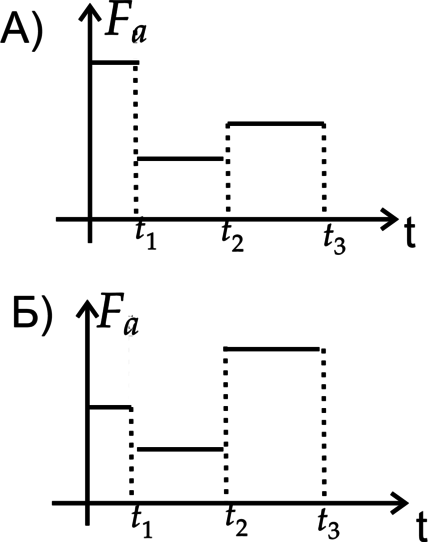
ПОЛЕДОВАТЕЛЬНОСТЬ
1) \(\rho_1\), \(\rho_2\), \(\rho_3\)
2) \(\rho_2\), \(\rho_3\), \(\rho_1\)
3) \(\rho_2\), \(\rho_1\), \(\rho_3\)
4) \(\rho_3\), \(\rho_1\), \(\rho_2\)
Сила Архимеда рассчитывается по формуле \(F_a=\rho g V\), где \(\rho\) — плотность жидкости. \(V\) — объем погруженной части тела. Так как \(V\) везде одинаковый, то \(F_a\) зависит только от \(\rho\).
А) До \(t_1\) \(F_a\) максимальна, а значит первым идет жидкость с плотностью \(\rho_3\). На втором этапе сила Архимеда минимальна, следовательно, плотность жидкости \(\rho_1\). Последняя жидкость \(\rho_2\). Ответ – 4
Б) Первый этап — \(F_a\) принимает среднее значение, значит жидкость с плотностью \(\rho_2\), второй — минимальное, значит — \(\rho_1\). Третья жидкость с максимальной плотностью — \(\rho_3\). Ответ– 3
Тело массой \(m\) и объёмом \(V\) плавает на поверхности жидкости плотностью \(\rho\). Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
\[\begin{array}{ll} \text{Физические величины}&\text{Формула}\\ \text{А) Сила Архимеда } &1)\ \rho g V \\ \text{Б) Объём погружённой части тела } &2)\ V \\ &3)\ mg \\ &4)\ \dfrac{m}{\rho} \\ \end{array}\]
\[\begin{array}{|c|c|} \hline \text{А}&\text{Б}\\ \hline &\\ \hline \end{array}\]
А) Так как тело плавает на поверхности воды, то сила Архимеда уравновешивает силу тяжести, значит \(F_a=mg\). Ответ – 3
Б) Выразим объем погруженной части \(V_\text{п} \) из \(F_a=\rho g V_\text{п}= mg\), значит \(V_\text{п}=\dfrac{m}{\rho}\). Ответ – 4
Тело массой \(m\) и объёмом \(V\) лежит на дне сосуда с жидкостью плотностью \(\rho\). Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
\[\begin{array}{ll} \text{Физические величины}&\text{Формула}\\ \text{А) Сила Архимеда } &1)\ \rho g V \\ \text{Б) Разность силы тяжести и силы Архимеда } &2)\ g(\rho \cdot V - m) \\ &3)\ 0 \\ &4)\ g(m - \rho \cdot V ) \\ \end{array}\]
\[\begin{array}{|c|c|} \hline \text{А}&\text{Б}\\ \hline &\\ \hline \end{array}\]
А) Так как тело лежит на дне сосда, то оно погружено на весь свой объем в жидкость и сила Архимеда находится по формуле: \(F_a=\rho g V\). Ответ – 1
Б) Разность силы тяжести и силы Архимеда в этом случае \(g(m - \rho \cdot V) \). Так как тело погружено на весь свой объем. Ответ – 4



