Молекулярно-кинетическая теория
Готовиться с нами - ЛЕГКО!

На рисунке показан график циклического процесса, проведённого с одноатомным идеальным газом, в координатах \(V-T\), где \(V\) — объём газа, \(T\) — абсолютная температура газа. Количество вещества газа постоянно. 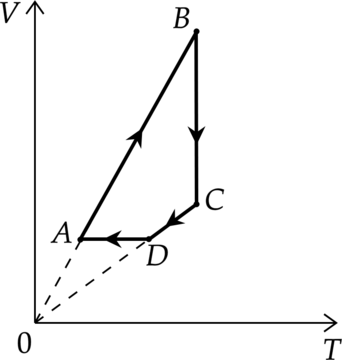
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике, и укажите их номера.
1) В состоянии \(B\) концентрация газа максимальна.
2) В процессе \(AB\) газ отдаёт некоторое количество теплоты.
3) В процессе \(BC\) внутренняя энергия газа увеличивается.
4) Давление газа в процессе \(CD\) постоянно, при этом внешние силы совершают над газом положительную работу.
5) В процессе \(DA\) давление газа изохорно уменьшается.
1) В точке \(B\) объем максимален, а концентрация минимальна:
Утверждение 1 —\(\color{red}{\small\text{Неверно }}\)
2) Первое начало термодинамики: \[Q=\Delta U+A\] где \(\Delta U\) — изменение внутренней энергии, \(A\) — работа газа, \(Q\) — количество теплоты, полученное газом. В процессе \(AB\) работа равна \(0\), температура увеличивается, то есть \(\Delta U>0\), значит \(Q>0\), то есть газ получает тепло
Утверждение 2 — \(\color{red}{\small\text{Неверно }}\)
3) Процесс \(BC\) — изотермический. Внутренняя энергия не меняется.
Утверждение 3 — \(\color{red}{\small\text{Неверно }}\)
4) Процесс \(СD\) — изобарное сжатие. При уменьшении объема внешние силы совершают положительную работу.
Утверждение 4 — \(\color{green}{\small\text{Верно }}\)
5) Процесс \(DA\) — изохорное охлаждение (\(p\sim T\)). Следовательно, при уменьшении температуры давление уменьшается.
Утверждение 5 — \(\color{green}{\small\text{Верно }}\)
Идеальный газ перевели из состояния 1 в состояние 3 так, как показано на графике зависимости давления р газа от объёма V. Количество вещества газа при этом не менялось. 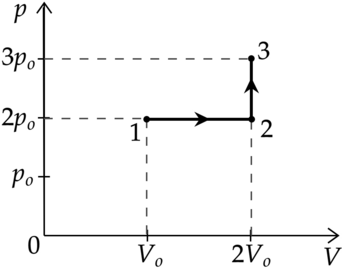
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике.
1)Абсолютная температура газа минимальна в состоянии 2.
2)В процессе 1-2 абсолютная температура газа уменьшилась в 2 раза.
3)В процессе 2-3 абсолютная температура газа уменьшилась в 1,5 раза.
4)Плотность газа максимальна в состоянии 1.
5)В ходе процесса 1-2-3 средняя квадратичная скорость теплового движения молекул газа увеличилась в \(\sqrt{3}\) раза.
1) Уравнение состояния газа: \[pV=\nu RT\] где \(p\) — давление газа, \(V\) — объем, занимаемый газом, \(\nu\) — количество вещеста, \(R\) — универасальная газовая постоянная, \(T\) — температура. Температура максимальна там, где максимально произведение \(pV\), поэтому из графика видно, что \(T_1 - min\), \(T_3 - max\), \(T_1<T_2<T_3\)
Утверждение 1 — \(\color{red}{\small\text{Неверно }}\)
2) Процесс 1-2 — изобарное расширение (\(V\sim T\)). Объем увеличился в 2 раза, то есть температура тоже увеличилась в 2 раза.
Утверждение 2 — \(\color{red}{\small\text{Неверно }}\)
3) Процесс 2-3 — изохорное нагревание. \(V=const\), следовательно \(p\sim T\) Давление увеличивается в 1,5 раза, то есть температура тоже увеличивается в 1,5 раза.
Утверждение 3 — \(\color{red}{\small\text{Неверно }}\)
4) В точке 1 — объем минимален, следовательно, плотность там максимальна.
Утверждение 4 — \(\color{green}{\small\text{Верно }}\)
5) \[E_{k}=\dfrac{3}{2}kT\] \[\dfrac{m_0 v^2}{2}=\dfrac{3}{2}kT\] где \(m_0\) — масса газа, \(v^2\) средняя квадратичная скорость \[v^2\sim T\] \[v\sim \sqrt{T}\] Температура в процессе 1-2-3 увеличилась в 3 раза, значит средняя квадратичная скорость увеличилась в \(\sqrt{3}\) раз
Утверждение 5 — \(\color{green}{\small\text{Верно }}\)
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В левой части сосуда содержится 40 г неона, в правой — 2 моль гелия. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул неона. Температура газов одинакова и остаётся постоянной.
Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Внутренняя энергия гелия в сосуде меньше, чем внутренняя энергия неона.
2) Концентрация гелия в левой части сосуда в 2 раза больше концентрации неона.
3) В левой части сосуда общее число молекул газов в 3 раза больше, чем в правой части.
4) Внутренняя энергия гелия в сосуде в конечном состоянии меньше, чем в начальном.
5) В конечном состоянии давление в левой части сосуда в 3 раза больше, чем в правой.
1) Молярная масса неона \(M=20\) г/моль. Количество неона: \[\nu=\dfrac{m}{M}=\dfrac{40\text{ г}}{20\text{ г/моль}}=2 \text{ моль}\] Гелий займет все пространство сосуда, значит в левой части будет 3 моля вещества (1 моль гелия и 2 моль неона).
В правой части будет тоже 1 моль гелия.
Внутренняя энергия газа: \[U=\dfrac{i}{2}\nu RT\] Газы находятся при одинаковой температуре, количество гелия равно количеству неона. Внутренняя энергия гелия равна внутренней энергии неона
Утверждение 1 — \(\color{red}{\small\text{Неверно }}\)
2) В левой части сосуда количество гелия в два раза меньше количества неона. Следовательно, концентрация гелия в два раза меньше концентрации неона.
Утверждение 2 — \(\color{red}{\small\text{Неверно }}\)
3) Так как количество вещества в левой части сосуда больше в 3 раза, чем в правой, то и количество молекул также больше в 3 раза.
Утверждение 3 — \(\color{green}{\small\text{Верно }}\)
4) Так как температура гелия и общее количество гелия в сосуде не изменилось, то и внутреннняяя энергия не поменялась.
Утверждение 4 — \(\color{red}{\small\text{Неверно }}\)
5) Давление газа: \[p=nkT\] Так как кол-во вещества в левой части сосуда больше в 3 раза, чем в правой, температуры одинаковые, то давление в конечном состоянии больше в левой части в 3 раза, чем в правой.
Утверждение 5 — \(\color{green}{\small\text{Верно }}\)
Объём сосуда с идеальным газом увеличили вдвое и добавили в сосуд такое же количество того же газа. Температура в сосуде поддерживается постоянной.
Выберите два верных утверждения, описывающих этот процесс.
1) Давление газа в этом процессе увеличилось в 4 раза.
2) Внутренняя энергия газа в сосуде увеличилась.
3) Концентрация молекул газа в сосуде уменьшилась.
4) Давление газа в результате этого процесса не изменилось.
5) Плотность газа в сосуде увеличилась.
1) Уравнение состояния газа: \[pV=\nu RT\] \[p=\dfrac{\nu RT}{V}\] где \(\nu\) — количество вещества, \(T\) — температура в Кельвинах, \(p\) — давление газа, \(V\) — объем, занимаемый газом, \(R\) — универсальная газовая постоянная. Так как и числитель, и знаменатель увеличился в 2 раза, то давление газа не изменится.
Утверждение 1 — \(\color{red}{\small\text{Неверно }}\)
2) Внутренняя энергия газа: \[U=\dfrac{i}{2}\nu RT\] Температура не изменилась, количество газа увеличилось, следовательно, внутренняя энергия газа увеличилась.
Утверждение 2 — \(\color{green}{\small\text{Верно }}\)
3) \(p=nkT\) где \(n\) — концентрация молекул. Из этой формулы видно, что концентрация не изменилась.
Утверждение 3 — \(\color{red}{\small\text{Неверно }}\)
4) По пункту 1, утверждение 4 — \(\color{green}{\small\text{Верно }}\)
5) Плотность газа: \[\rho=\dfrac{p\mu}{RT}\] где \(\mu\) — молярная масса газа. Давление, молярная масса и температура газа не изменились, поэтому плотность тоже не изменится.
Утверждение 5 — \(\color{red}{\small\text{Неверно }}\)
Идеальный газ переводят из состояния 1 в состояние 3 так, как показано на графике зависимости давления \(р\) газа от объёма \(V\). Количество вещества газа при этом не меняется. 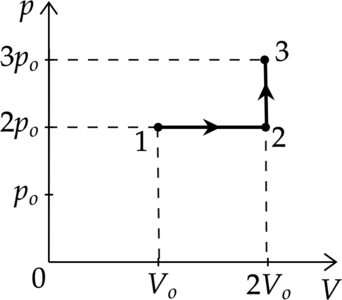
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике, и укажите их номера.
1) Абсолютная температура газа максимальна в состоянии 1.
2) В процессе 1-2 абсолютная температура газа изобарно увеличилась в 2 раза.
3) В процессе 2-3 абсолютная температура газа изохорно увеличилась в 1,5 раза.
4) Плотность газа минимальна в состоянии 1.
5) В ходе процесса 1-2-3 средняя квадратическая скорость теплового движения молекул газа увеличивается в 6 раз.
1) Уравнение состояния газа: \[pV=\nu RT\] где \(\nu\) — количество вещества, \(T\) — температура в Кельвинах, \(p\) — давление газа, \(V\) — объем, занимаемый газом, \(R\) — универсальная газовая постоянная. Температура максимальна там, где максимально произведение \(pV\), поэтому из графика видно, что \(T_1 - min\), \(T_3 - max\)
Утверждение 1 — \(\color{red}{\small\text{Неверно }}\)
2) Процесс 1-2 — изобарное расширение (\(V\sim T\)). Объем увеличился в 2 раза, то есть температура тоже увеличилась в 2 раза.
Утверждение 2 — \(\color{green}{\small\text{Верно }}\)
3) Процесс 2-3 — изохорное нагревание. \(V=const\), следовательно \(p\sim T\) Давление увеличивается в 1,5 раза, то есть температура тоже увеличивается в 1,5 раза.
Утверждение 3 — \(\color{green}{\small\text{Верно }}\)
4) В точке 1 — объем минимален, следоваельно, плотность там максимальна. Утверждение 4 — \(\color{red}{\small\text{Неверно }}\)
5) \[E_{k}=\dfrac{3}{2}kT\] \[\dfrac{m_0 v^2}{2}=\dfrac{3}{2}kT\] \[v^2\sim T\] \[v\sim \sqrt{T}\] Температура в процессе 1-2-3 увеличилась в 3 раза, значит средняя квадратичная скорость увеличилась в \(\sqrt{3}\) раз
Утверждение 5 —\(\color{red}{\small\text{Неверно }}\)
В ходе адиабатного процесса внутренняя энергия 2 моль разреженного аргона уменьшилась.
Выберите из предложенного перечня два верных утверждения, верно описывающие данный процесс, и укажите их номера.
1) Температура газа в ходе процесса увеличилась.
2) В ходе процесса газ расширился, совершив работу.
3) Давление газа в течение всего процесса остаётся неизменным.
4) Концентрация молекул газа в ходе процесса уменьшилась.
5) Объём газа в ходе процесса уменьшается.
1) Внутренняя энергия: \[U=\dfrac{i}{2}\nu RT\] где \(\nu\) — количество вещества, \(T\) — температура в Кельвинах \(i\) — количество степеней свободы газа. Внутренняя энергия уменьшается, следовательно, температура уменьшается.
Утверждение 1 — \(\color{red}{\small\text{Неверно }}\)
2) Первое начало термодинамики: \[Q=\Delta U+A\] где \(\Delta U\) — изменение внутренней энергии, \(A\) — работа газа, \(Q\) — количество теплоты, полученное газом. Процесс — адиабатический, то есть \(Q=0\) \(A=-\Delta U\), \(\Delta U<0\), значит \(-\Delta U>0\), \(A>0\)
Утверждение 2 — \(\color{green}{\small\text{Верно }}\)
3) При адиабатном процессе давление изменяется
Утверждение 3 — \(\color{red}{\small\text{Неверно }}\)
4) \(A>0\), то есть газ расширяется, объем увеличивается. Концентрация молекул: \[n=\dfrac{N}{V}\] где \(N\) — количество молекул, \(V\) — объем, занимаемый молекулами. Знаменатель увеличивается, значит, концентрация уменьшается.
Утверждение 4 — \(\color{green}{\small\text{Верно }}\)
5) \(A>0\), то есть газ расширяется, объем увеличивается.
Утверждение 5 —\(\color{red}{\small\text{Неверно }}\)
При переводе одноатомного идеального газа из состояния 1 в состояние 2 давление p пропорционально концентрации его молекул n (см. рисунок). Масса газа в процессе остаётся постоянной. 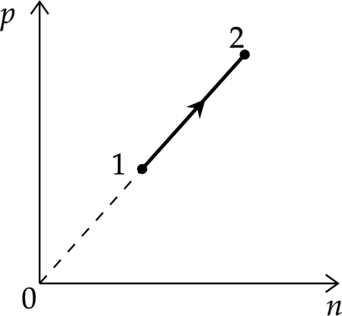
Из приведённого ниже списка выберите два правильных утверждения, характеризующих процесс 1-2.
1) Абсолютная температура газа увеличивается.
2) Происходит изотермическое расширение газа.
3) Среднеквадратическая скорость теплового движения молекул газа увеличивается.
4) Плотность газа увеличивается.
5) Средняя кинетическая энергия теплового движения молекул газа остаётся неизменной.
1) \[p=nkT\] где \(n\) — концентрация молекул, \(T\) — температура в Кельвинах, \(p\) — давление газа. Из графика видно, что \(p\sim n\), значит, процесс происходит при постоянной температуре (\(T=const\))
Утверждение 1 — \(\color{red}{\small\text{Неверно }}\)
2) Концентрация в процессе увеличивается \[n=\dfrac{N}{V}\] где \(N\) — количество молекул, \(V\) — объем, занимаемый молекулами. Из этого следут, что объем в процессе уменьшался, т.е. газ изотермически сжимают
Утверждение 2 — \(\color{red}{\small\text{Неверно }}\)
3) Кинетическая энергия находится по формуле: \[E_{k}=\dfrac{3}{2}kT\] \[\dfrac{m_0 v^2}{2}=\dfrac{3}{2}kT\] \[v^2\sim T\] Температура не меняется, следовательно, средняя квадратичная скорость тоже не меняется
Утверждение 3 — \(\color{red}{\small\text{Неверно }}\)
4) Плотность равна: \[\rho=\dfrac{m}{V}\] Объем в этом процессе уменьшается, масса не изменяется, следовательно, плотность увеличивается.
Утверждение 4 — \(\color{green}{\small\text{Верно }}\)
5) \(T=const\) \[E_{k}=\dfrac{3}{2}kT\] \[E_{k}=const\]
Утверждение 5 — \(\color{green}{\small\text{Верно }}\)



