Молекулярно-кинетическая теория (страница 2)
Готовиться с нами - ЛЕГКО!

Один моль идеального одноатомного газа совершает циклический процесс 1-2-3-4-1, график которого показан на рисунке в координатах \(p-V\). 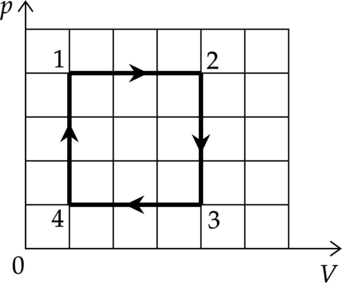
Из предложенного перечня утверждений выберите два правильных и укажите их номера.
1) В процессе 1-2 внутренняя энергия газа увеличивается.
2) В процессе 2-3 газ совершает положительную работу.
3) В процессе 3-4 газу сообщают положительное количество теплоты.
4) В процессе 4-1 температура газа увеличивается в 4 раза.
5) Работа, совершённая газом в процессе 1-2, в 3 раза больше работы, совершённой над газом в процессе 3-4.
1) Внутренняя энергия газа: \[U=\dfrac{i}{2}\nu RT\] где \(\nu\) — количество вещества, \(T\) — температура в Кельвинах, \(R\) — универсальная газовая постоянная, \(i\) — количество степеней свободы газа. В процессе 1-2 температура увеличивается (изобарное расширение), значит внутренняя энергия тоже увеличивается
Утверждение 1 — \(\color{green}{\small\text{Верно }}\)
2) Процесс 2-3 — изохорное охлаждение. При постоянном объеме работа газа равна 0.
Утверждение 2 — \(\color{red}{\small\text{Неверно }}\)
3) Первое начало термодинамики: \[Q=\Delta U+A\] где \(\Delta U\) — изменение внутренней энергии, \(A\) — работа газа, \(Q\) — количество теплоты, полученное газом. В процессе 3-4 \(\Delta U<0\), \(A<0\), следовательно \(Q<0\)
Утверждение 3 — \(\color{red}{\small\text{Неверно }}\)
4) Процесс 4-1 — изохорное нагревание (\(p\sim T\)). Давление увеличивается в 4 раза, значит температура тоже увеличивается в 4 раза. Объем в этом процессе уменьшается, масса не изменяется, следовательно плотность увеличивается.
Утверждение 4 — \(\color{green}{\small\text{Верно }}\)
5) Работа — площадь под графиком в координтах \(p-V\), площадь в процессе 1-2 в 4 раза больше площади 4-3
Утверждение 5 — \(\color{red}{\small\text{Неверно }}\)
В ходе адиабатного процесса внутренняя энергия 1 моль разреженного гелия увеличивается. 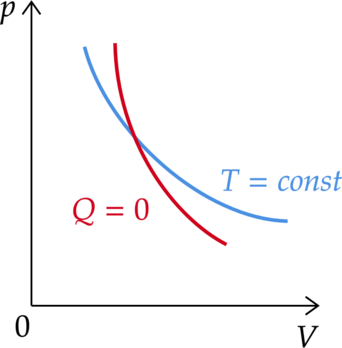
Выберите из предложенного перечня два верных утверждения, верно описывающие данный процесс, и укажите их номера.
1) Давление газа в ходе процесса увеличилось.
2) Объём газа в этом процессе остаётся неизменным.
3) Газ сжали, совершив над ним работу.
4) Температура газа в ходе процесса уменьшается.
5) Концентрация молекул газа в ходе процесса уменьшилась.
1) Так как в адиабатическом процессе увеличивается внутренняя энергия, то температура тоже увеличивается. (Адиабата на графике более “крутая”, чем изотерма, значит процесс идет с увеличением давления и уменьшением объема)
Утверждение 1 — \(\color{green}{\small\text{Верно }}\)
2) Объем в процессе уменьшается
Утверждение 2 — \(\color{red}{\small\text{Неверно }}\)
3) Так как газ сжимается, то над ним совершают работу
Утверждение 3 — \(\color{green}{\small\text{Верно }}\)
4) Температура увеличивается. Утверждение 4 — \(\color{red}{\small\text{Неверно }}\)
5) Концентрация: \[n=\dfrac{N}{V}\] При уменьшении объема увеличивается концентрация.
Утверждение 5 —\(\color{red}{\small\text{Неверно }}\)
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). Газ нагревают.

Выберите из предложенного перечня два верных утверждения, верно описывающие данный процесс, и укажите их номера.
1) Объём газа в этом процессе остаётся неизменным.
2) Давление газа в сосуде остаётся неизменным.
3) Плотность газа в этом процессе увеличивается.
4) Сила Архимеда, действующая на шарик, уменьшается.
5) Концентрация молекул газа в сосуде увеличивается.
1) Так как поршень подвижный (не закреплен), то процесс будет происходить при постоянном давлениии.
Уравнение состояния газа: \[pV=\nu RT\] где \(\nu\) — количество вещества, \(T\) — температура в Кельвинах, \(p\) — давление газа, \(V\) — объем, занимаемый газом, \(R\) — универсальная газовая постоянная. Выразим объем \[V=\dfrac{\nu RT}{p}\] При нагревании газа объем увеличивается.
Утверждение 1 — \(\color{red}{\small\text{Неверно }}\)
2) Утверждение 2 — \(\color{green}{\small\text{Верно }}\)
3) Плотность газа: \[\rho=\dfrac{m}{V}\] При нагревании объем увеличивается, значит плотность уменьшается.
Утверждение 3 — \(\color{red}{\small\text{Неверно }}\)
4) Сила Архимеда: \[F_{\text{Арх}}=\rho gV\] где \(\rho\) — плотность газа, \(V\) — объем шарика, \(g\) — ускорение свободного падения. Плотность уменьшается, значит, сила Архимеда уменьшается.
Утверждение 4 — \(\color{green}{\small\text{Верно }}\)
5) Концентрация: \[n=\dfrac{N}{V}\] При нагревании газа объем увеличивается, концентрация уменьшается.
Утверждение 5 — \(\color{red}{\small\text{Неверно }}\)
На \(pV\)—диаграмме отображена последовательность трёх процессов (1 — 2 — 3) изменения состояния 2 моль идеального газа. 
Из предложенного перечня утверждений выберите два правильных и укажите их номера.
1) В процессе 1 газ отдаёт положительное количество теплоты.
2) Процесс 2 является изотермическим.
3) В процессе 3 газ совершает работу.
4) В процессе 2 происходит расширение газа при постоянной температуре.
5) В процессе 1 происходит сжатие газа при постоянной температуре.
Работа газа находится как площадь под графиком 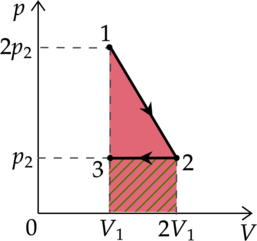
1) Первое начало термодинамики: \[Q=\Delta U+A\] где \(\Delta U\) — изменение внутренней энергии, \(A\) — работа газа, \(Q\) — количество теплоты, полученное газом. \(\Delta U=0\), так как температура в процессе 1 не изменяется. При увеличении давления в изотермическом процессе объём уменьшается. \(\Delta V<0\), следоватлеьно, \(A<0\). Таким образом, \(Q<0\), то есть газ отдает кол-во теплоты в данном процессе.
Утверждение 1 — \(\color{green}{\small\text{Верно }}\)
2) В процессе 2 температура увеличивается.
Утверждение 2 — \(\color{red}{\small\text{Неверно }}\)
3) \(p=const\), следовательно \(V\sim T\)
Температура уменьшается, то есть объем тоже уменьшается, \(\Delta V<0\), \(A<0\)
Утверждение 3 — \(\color{red}{\small\text{Неверно }}\)
4) В процессе 2 температура увеличивается.
Утверждение 4 — \(\color{red}{\small\text{Неверно }}\)
5) Температура в процессе 1 не изменяется. По закону Бойля-Мариотта \(p V=const\) так как давление увеличивается объём уменьшается.
Утверждение 5 —\(\color{green}{\small\text{Верно }}\)
На рисунке показана зависимость давления газа \(p\) от его плотности \(\rho\) в циклическом процессе, совершаемом 2 моль идеального газа в идеальном тепловом двигателе. Цикл состоит из двух отрезков прямых и четверти окружности.
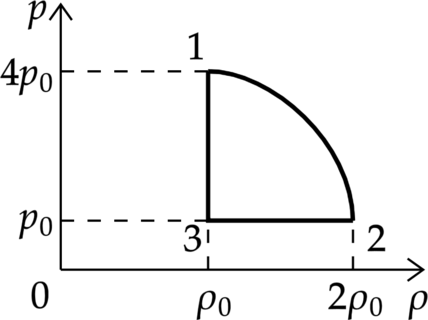
На основании анализа этого циклического процесса выберите два верных утверждения.
1) В процессе 1−2 температура газа уменьшается.
2) В состоянии 3 температура газа максимальна.
3) В процессе 2−3 объём газа уменьшается.
4) Отношение максимальной температуры к минимальной температуре в цикле равно 8.
5) Работа газа в процессе 3−1 положительна.
“Демоверсия 2017”
1) По уравнению Клапейрона – Менделеева: \[p=\dfrac{\rho}{\mu}RT,\] где \(T\) – температура, \(\mu\) – молярная масса газа.
Давление уменьшилось в 4 раза, а плотность увеличилась в 2 раза, следовательно, температура уменьшилась в 8 раз.
Утверждение 1 – \(\color{green}{\small \text{Верно}}\)
2) Аналогично предыдущему пункту \[p=\dfrac{\rho}{\mu}RT\] Максимальная температура будет в состоянии 1 (давление максимально, плотность минимальна)
Утверждение 2 – \(\color{red}{\small \text{Неверно}}\)
3) В процессе 2 – 3 плотность меньшается, а по формуле: \[\rho =\dfrac{m}{V}\] Объем увеличивается
Утверждение 3 – \(\color{red}{\small \text{Неверно}}\)
4) Аналогично пункту 2, минимальность температуры будет достигнута в точке с наименьшим давлением и наибольшей плотностью (т. 2), а отношение температур действительно равно 8
Утверждение 4 – \(\color{green}{\small \text{Верно}}\)
5) В процессе 2 – 3 плотность постоянна, следовательно, объем постоянен и газ не совершает работу.
Утверждение 5 – \(\color{red}{\small \text{Неверно}}\)
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В начальный момент времени в левой части сосуда содержится 4 моль гелия, в правой – 40 г аргона. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул аргона. Температура газов одинаковая и остаётся постоянной. Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Концентрация гелия в правой части сосуда в 2 раза меньше, чем аргона.
2) Отношение давления газов в правой части сосуда к давлению газа в левой части равно 1,5.
3) В правой части сосуда общее число молекул газов меньше, чем в левой части.
4) Внутренняя энергия гелия и аргона одинакова.
5) В результате установления равновесия давление в правой части сосуда увеличилось в 3 раза.
“Демоверсия 2020”
Перегородка проницаема только для молекул гелия, поэтому в результате установления равновесия парциальное давление гелия в левой части будет равно парциальному давлению гелия в правой части. Давление газа можно вычислить по формуле: \[p=\dfrac{\nu R T}{V}\] Парциальные давления гелия в левой и правой части одинаковы, одинаковы температуры и объёмы частей, следовательно, одинаковы и количества вещества гелия в левой и правой частях сосуда, то есть в левой и правой части сосуда будет содержаться по 2 моля гелия.
Найдём связь концентрации и количества вещества: \[n=\dfrac{N}{V}=\dfrac{\nu N_A}{V}\] То есть концентрации и количества вещества зависят прямо пропорционально друг от друга, также заметим, что чем больше количество вещества, тем больше и количество молекул.
Найдём количество вещества аргона: \[\nu_{Ar}=\dfrac{m_{Ar}}{\mu_{Ar}}=\dfrac{40\text{ г}}{40\text{ г/моль}}=1\text{ моль}\]
Используя полученное выше, рассмотрим данные в задании утверждения.
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
1) \(\color{red}{\small \text{Неверно}}\)
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
2) \(\color{green}{\small \text{Верно}}\)
Отношение давлений: \[\dfrac{p_\text{ п}}{p_\text{ л}}=\dfrac{\nu_\text{ г.п}+\nu_{Ar}}{\nu_\text{ г.л}}=\dfrac{2\text{ моль}+1\text{ моль}}{2\text{ моль}}=1,5\] Где \(\nu_{\text{ г.п.}},\nu_{\text{ г.л.}}\) – количество вещества гелия в правой части, количество вещества гелия в левой части соответственно.
3) \(\color{red}{\small \text{Неверно}}\)
Количество вещества газов в правой части сосуда больше количества вещества газа в левой части сосуда, следовательно, в правой части сосуда общее число молекул газа больше, чем в левой части сосуда.
4) \(\color{red}{\small \text{Неверно}}\)
Внутренняя энергия одноатомного идеального газа может быть вычислена по формуле: \[U=\dfrac{3}{2}\nu R T\] Температура газов одинакова. Количество вещества гелия больше количества вещества аргона, следовательно, внутренняя энергия гелия больше внутренней энергии аргона.
5) \(\color{green}{\small \text{Верно}}\)
айдём отношение конечного давления в правой части сосуда к начальному давлению в правой части сосуда: \[\dfrac{p_{k}}{p_\text{ н}}=\dfrac{\nu_{\text{ г.п.}}+\nu_{Ar}}{\nu_{Ar}}=\dfrac{2\text{ моль}+1\text{ моль}}{1\text{ моль}}=3\]


