Механические колебания (страница 2)
Готовиться с нами - ЛЕГКО!

На рисунках даны зависимости координаты Х от времени t двух грузов, подвешанных на лёгкие пружины. Найдите отношение периодов \(\dfrac{T_1}{T_2}\) маятников.
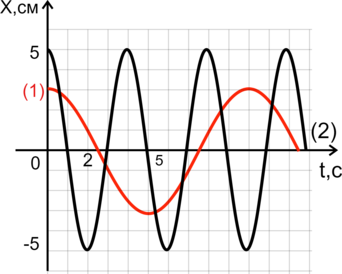
По графику видно, что период первого груза \(T_1=10\) с, а период второго \(T_2=4\) с.
Тогда нужное нам отношение равно: \[\frac{T_1}{T_2}=\frac{10\text{ с}}{4\text{ с}} = 2,5\]
На рисунке приведён график зависимости координаты Х математического маятика от времени t. Чему равен период колебаний? (Ответ дайте в секундах.) 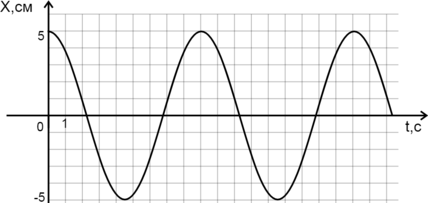
Период колебаний – наименьший промежуток времени, за который система совершает одно полное колебание. По графику видно, что период \(T=9\) c. 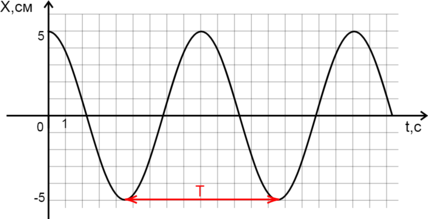
На рисунке приведён график зависимости координаты Х математического маятика от времени t. Чему равна амплитуда колебаний? (Ответ дайте в метрах.) 
Амплитуда колебаний - это максимальное отклонение тела от положения равновесия. По графику видно, что \(A=5\) см \(=0,05\) м. 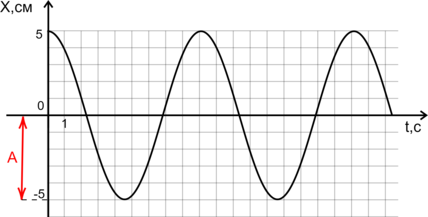
На рисунке приведён график зависимости координаты Х математического маятика от времени t. Чему равна частота колебаний? (Ответ дайте в Гц и округлите до сотых.) 

Частота колебаний – величина обратная периоду колебаний. По графику видно, что период колебаний \(T=9\) c. Значит: \[\nu=\frac{1}{T} = \frac{1}{9\text{ c}} = 0,1111\text{ Гц} \approx 0,11\text{ Гц }\]
Груз массой \(m_1=200\) г совершает свободные гармонические колебания на лёгкой пружине жёсткостью k. Каким должна быть масса \(m_2\) груза, чтобы на этой же пружине частота колебаний уменьшилась в два раза? (Ответ дайте в кг)
Частоту колебаний \(\nu\) можно найти по формуле: \[\nu = \frac{1}{2\pi}\cdot \sqrt{\frac{k}{m}}\]
Напишем это уравнение для \(\nu_1\) и \(\nu_2\): \[\begin{cases} \nu_1 = \dfrac{1}{2\pi}\cdot \sqrt{\dfrac{k}{m_1}} &\hspace{5mm}\quad(1)\\ \\ \nu_2 = \dfrac{1}{2\pi}\cdot \sqrt{\dfrac{k}{m_2}} &\hspace{5mm} \quad(2) \end{cases}\]
Поделив (1) на (2), получим: \[\frac{\nu_1}{\nu_2} =\sqrt{\frac{m_2}{m_1}} \Rightarrow m_2 =\frac{\nu_1^2}{\nu_2^2}\cdot m_1\] \[m_2 = \frac{(2\nu_2)^2}{\nu_2^2}\cdot m_1 =4m_1\] \[m_2 = 4\cdot 200\text{ г} = 800\text{ г} = 0,8\text{ кг}\]
На рисунке изображён график зависимости амплитуды колебаний А маятника от частоты силы \(\nu\), вызывающей эти колебания – резонансная кривая. Какой была частота в момент резонанса? (Ответ дайте в Гц) 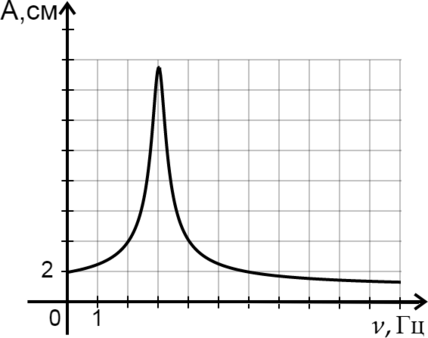
В момент резонанса амплитуда колебаний имеет наибольшее значение. По графику видно, что амплитуда максимальна, когда \(\nu=3\) Гц. 
На рисунке приведён график зависимсти скорости математического маятника \(v\) от времени \(t\). Масса тела 0,2 кг. Найдите максимальную кинетичекую энергию этого маятника. (Ответ дайте в Дж.)
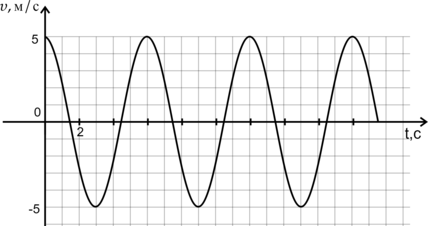
Формула кинетической энергии \(E_k\): \[E_k = \frac{m\upsilon^2}{2}\] Следовательно, \(E_k=E_{\text{kmax}}\), когда \(\upsilon = \upsilon_{\text{max}}\). По рисунку видно, что \(\upsilon_{\text{max}}=5\) м/с.
Значит, максимальная кинетическая энергия маятника равна: \[E_k = \frac{0,2\text{ кг }\cdot25\text{ м/c }^2}{2}\ = 2,5\text{ Дж }\]



