Первое начало термодинамики
Готовиться с нами - ЛЕГКО!

В процессе эксперимента внутренняя энергия газа увеличилась на \(4,7\) Дж, при этом газ отдал окружающей среде количество теплоты, равное \(39\) Дж. Какую работу совершили над газом внешние силы в данном эксперименте? Ответ дать в Дж.
По первому закону термодинамики: \[Q=\Delta U + A,\] где \(Q\) — количество теплоты (т.к. по условию газ отдает количество теплоты, то при подстановке значений мы будем писать его со знаком “\(-\)”), \(\Delta U\) — изменение внутренней энергии газа, а \(A\) — работа, совершенная газом.
Отсюда: \[A=Q-\Delta U~~~(1)\] Известно, что: \[A=-A_{\text{вн}},\] где \(A_{\text{вн}}\) — работа внешних сил над газом. Подставим сюда (1) и выразим \(A_{\text{вн}}\): \[A_{\text{вн}}=-A=-(Q-\Delta U)=-Q+\Delta U=-(-39\text{ Дж})+4,7\text{ Дж}=39\text{ Дж}+4,7\text{ Дж}=43,7\text{ Дж }\]
На \(pT\)-диаграмме показан процесс изменения состояния постоянной массы идеального газа. В этом процессе газ совершает работу, равную 3 кДж. Каково количество теплоты, полученное газом? (Ответ дайте в кДж.) 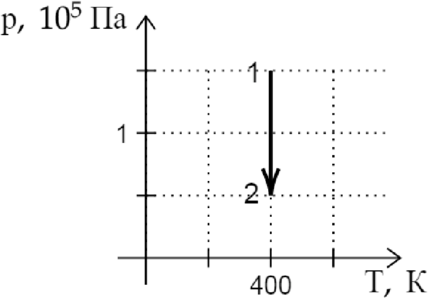
По первому закону термодинамики: \[Q=\Delta U + A,~~~(1)\] где \(Q\) — количество теплоты, полученное газом, \(\Delta U\) — изменение внутренней энергии газа, а \(A\) — работа, совершенная газом. \[\Delta U=\dfrac{3}{2}\nu R \Delta T.\] По графику находим, что \(\Delta T = 0\), значит \(\Delta U = 0\). Подставим это в (1): \[Q=A=3\text{ кДж }\]
Идеальный газ совершил работу 161 кДж и при этом внутренняя энергия газа уменьшилась на 140 кДж. Какое количество теплоты получил газ в этом процессе? (Ответ дать в кДж)
По первому закону термодинамики: \[Q=\Delta U + A,\] где \(Q\) — количество теплоты, полученное газом, \(\Delta U\) — изменение внутренней энергии газа, а \(A\) — работа, совершенная газом.
\[Q=-140\text{ кДж}+ 161\text{ кДж}=-140\cdot 10^3\text{ Дж}+ 161\cdot 10^3\text{ Дж}=21000\text{ Дж}=21\text{ кДж }\]
На рисунке показан график изменения состояния постоянной массы идеального газа. В этом процессе газ принял количество теплоты, равное 4 кДж. На сколько увеличилась внутренняя энергия газа? Ответ дайте в кДж. 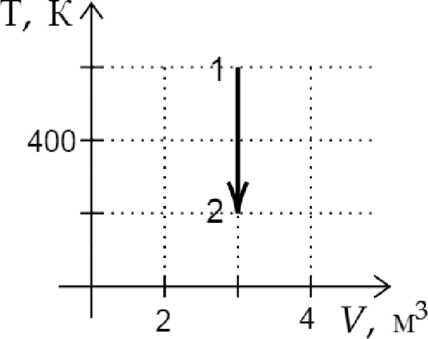
Из графика видно, что данный процесс является изохорным. Поскольку объем газа не изменялся, газ не совершал работы. Следовательно, согласно первому началу термодинамики: \[Q=\Delta U=4\text{ кДж }\]
В некотором процессе газ получает количество теплоты 97 Дж, внутренняя энергия газа увеличивается, причём изменение его внутренней энергии составляет 4/7 от работы газа. Какую работу совершает газ в этом процессе? Ответ дать в Дж и округлить до целых.
По первому закону термодинамики: \[Q=\Delta U + A,\] где \(Q\) — количество теплоты, полученное газом, \(\Delta U\) — изменение внутренней энергии газа, а \(A\) — работа, совершенная газом.
По условию \(\Delta U=\dfrac{4}{7}A\). Отсюда: \[Q=\dfrac{4}{7}A + A=\dfrac{11}{7}A\] \[A=\dfrac{7}{11}Q=\dfrac{7}{11}\cdot 97\text{ Дж}\approx 62\text{ Дж }\]
В процессе адиабатного расширения четырех молей идеального одноатомного газа газ совершил работу 100 Дж. Определите изменение внутренней энергии газа в этом процессе.
По первому закону термодинамики: \[Q=\Delta U + A\] В адиабатном процессе газ не получает теплоты от внешней среды: \[0=\Delta U + A \Rightarrow \Delta U=-A=-100\text{ Дж }\]
В некотором процессе идеальный газ совершает работу 140 Дж, причем полученное газом количество теплоты составляет 16/7 от изменения внутренней энергии газа (внутреняя энергия увеличивается). Чему равно изменение внутренней энергии газа в этом процессе? Ответ округлить до целых.
По первому закону термодинамики: \[Q=\Delta U + A,\] где \(Q\) — количество теплоты, полученное газом, \(\Delta U\) — изменение внутренней энергии газа, а \(A\) — работа, совершенная газом.
По условию \(Q=\dfrac{16}{7} \Delta U\). Отсюда: \[\dfrac{16}{7} \Delta U=\Delta U + A\] \[A=\dfrac{9}{7}\Delta U\Rightarrow \Delta U=\dfrac{7}{9}A=\dfrac{7}{9}\cdot 140\text{ Дж}\approx 109\text{ Дж }\]



