физика (страница 2)

В инерциальной системе отсчета сила \({\vec F}\) сообщает телу массой \(m\) ускорение \({\vec a}\). Модуль ускорения равен \(a=2\, \text{м/с}^2\). Определите модуль ускорения, которое сообщается телу массой \(4m\) модулем силы \(5F\) в этой системе отсчета.
Воспользуемся вторым законом Ньютона для двух случаев: \[{\vec F}=m{\vec a}\] \[5{\vec F}=4m{\vec a_1},\] где \(a_1\) - искомое ускорение Для нахождения \(a_1\) поделим уравнения: \[\frac{F}{5F}=\frac{ma}{4ma_1}\] \[a_1=\frac{5a}4=\frac{5\cdot 2}4=2,5 \text{ м/с}^2\]
В инерциальной системе отсчета сила \(\Vec{F}\) сообщает телу массой \(m\) равное по модулю 4 м/с\(^2\). Во сколько раз масса второго тела меньше массы первого, если ускорение второго тела \(a_{2}\)=16 м/c\(^2\) под действием силы \(2\Vec{F}\) в этой системе отсчета
В инерциальной системе отсчета тело движется по 2 закону Ньютона: \[F=m \cdot a\] где \(m\) масса тела, а \(a\) - его ускорение
Для первого случая: \[{F}=4m_{1} \quad (1)\]
Для второго случая: \[{2F}=16m_{2} \quad (2)\]
Подставим (1) в (2), получим: \[8m_{1}=16m_{2}\]
\[m_{1}=2m_{2}\]
Следовательно масса второго тела в 2 раза меньше массы первого тела
В инерциальной системе отсчета сила \(F\) сообщает телу массой \(m\) ускорение 9 м/c\(^2\).
Какое ускорение сообщает сила 1/3 F в этой же системе отсчета телу массой \(3m\)
В инерциальной системе отсчета тело движется по 2 закону Ньютона: \[F=m \cdot a\] где \(m\) масса тела, а \(a\) - его ускорение
Для первого случая: \[F=9m\] выразим \(m\): \[m=\frac{F}{9} \quad (1)\]
Запишем 2 закон Ньютона для второго случая: \[\frac{1}{3} F = 3m \cdot a_{2}\] выразим \(a_{2}\): \[a_{2} = \frac{F}{9m} \quad (2)\]
Подставим (1) в (2), получим: \[a_{2}=\frac{F}{9F}=1\]
Брусок покоится на наклонной плоскости, образующей угол \(a\)=\(30^{\circ}\), его масса \(m\)=0,1кг. Найдите силу трения покоя, которая действует на брусок
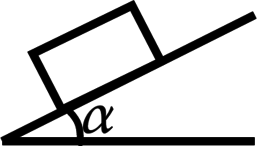
Отметим все силы, действующие на брусок, а также введем координатную плоскость. Ось \(x\) направим вдоль наклонной плоскости, а ось \(y\) перпендикулряно ей.
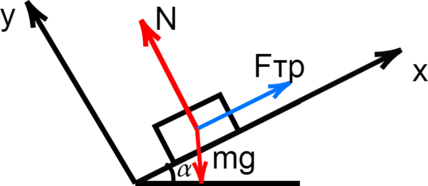
Запишем 2 закон Ньютона: \[F=m a\] где \(F\) – сумма всех сил, действующих на тело, \(a\) – его ускорение, \(m\) – масса тела
Так как брусок покоится, то его ускорение равно 0. Запишем 2 закон Ньютона на ось \(x\): \[F_{\text{тр}} -mg \sin a=0\]
Выразим \(F_{\text{тр}}\): \[F_{\text{тр}}=mg \sin a\]
Подставим числа из условия: \[F_{\text{тр}}=0,1 \text{ кг} \cdot 10 \text{ Н/кг} \cdot \frac{1}{2}=0,5\text{ Н}\]
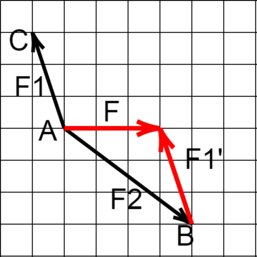
На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона клетки соответствует 1 Н. Определите модуль равнодействующей приложенных к телу сил.
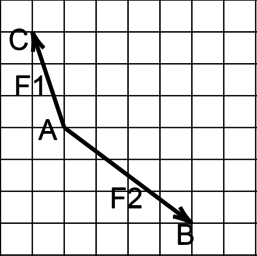
Построим вектор \(F1'\), который выходит из точки \(B\), параллельно вектору \(F1\)
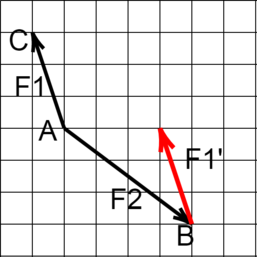
Соединим точку \(A\) с концом вектора \(F1'\). Получим искомый вектор \(F\)
При прямолинейном движении зависимость координаты тела \(x(t)\) имеет вид: \(x(t)=5+2t+4t^2\). Найдите координату, скорость и ускорение в момент времени \(t=2\) c при таком движении?
1 способ:
Проекция скорости — это производная соответствующей координаты по времени, проекция ускорения — это производная скорости по времени: \[\upsilon_x=x'(t)=(5+2t+4t^2)'=2+8t\] \[a_x=\upsilon_x'(t)=(2+8t)'=8\] Зная зависимость скорости и ускорения от времени, найдем координату, скорость и ускорение в момент времени \(t=2\) c \[x(2)=5+2\cdot2+4\cdot2^2=25\mbox{ м}\] \[\upsilon_x(2)=2+8\cdot2=18\mbox{ м/c}\] \[a_x(2)=8\mbox{ м/c$^2$}\]
2 способ:
Данная зависимость координаты от времени совпадает с зависимостью координаты от времени при равноускоренном движении: \(\displaystyle x(t)=x_0+\upsilon_{0x}t+\frac {a_xt^2}{2}\)
Сравнивая с выражением, данным в условии, получаем: \[x_0=5\mbox{ м}\quad\upsilon_{0x}=2\mbox{ м/с}\quad a_x=8\mbox{ м/с$^2$}\] \[x(2)=x_0+\upsilon_{0x}t+\frac {a_xt^2}{2}=5+2\cdot2+4\cdot2^2=25\mbox{ м}\] \[\upsilon_x(2)=\upsilon_{0x}+a_xt=2+8\cdot2=18\mbox{ м/c}\]
Охотник, стоящий на гладком льду, стреляет из ружья. Масса заряда 0,05 кг. Скорость снаряда 200 м/c. Какова масса охотника, если его скорость после выстрела равна 0,1 м/c.
Так как до выстрела общий импульс системы равен нулю, то по Закону Сохранения импульса: \[m_1\cdot v_1 - m_2\cdot _2 = 0\] где \(m_2\) – масса охотника, \(m_1\) – масса снаряда \(v_1\), \(v_2\) – скорости снаряда и охотника соответственно. \[m_2 = \frac {m_1 \cdot \upsilon_1} {\upsilon_2}\] \[m_2= \frac {0,05 \text{ кг} \cdot 200 \text{ м/с}}{0,1 \text{м/c}} =100 \text{ кг}\]



