Электродинамика

Электромагнитная индукция

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Электродинамика

Теоретическая справка

#614

Поток вектора магнитной индукции

Поток вектора магнитной индукции $Ф$ — физическая величина, численно равная скалярному произведению вектора магнитной индукции на вектор площади.

|------------------| -Ф-=-⃗B-⋅ ⃗S =-BS-cosα-

Единицы измерения: $[Ф ] =$ Вб (вебер).

Вектор площади $⃗ S$ сонаправлен с вектором нормали $⃗n$ и по модулю равен площади поверхности $S$ .

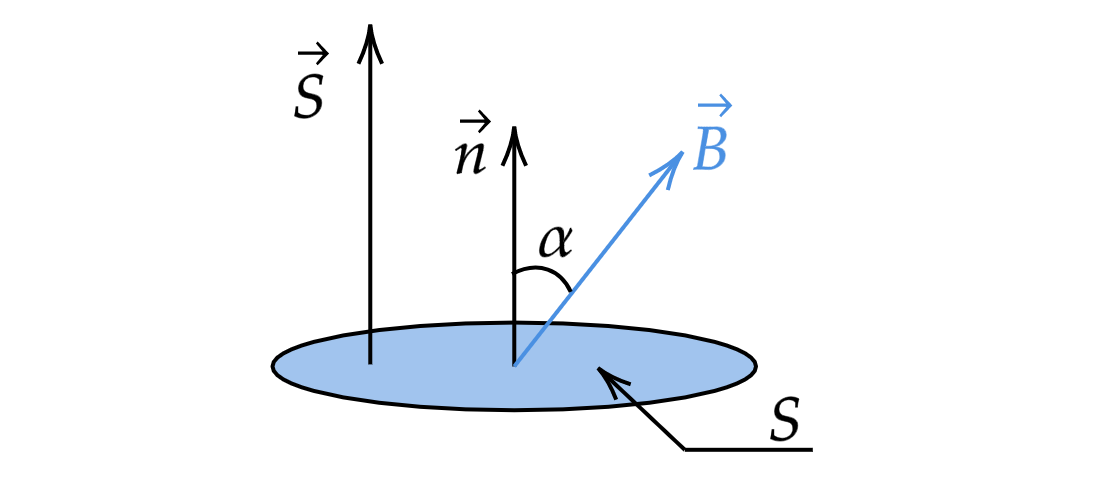
При $cos α = 0 ⇒ α = 90o$ поток вектора магнитной индукции равен нулю $Ф = 0$ . В этом случае магнитное поле лежит в плоскости контура (так как оно перпендикулярно вектору нормали $⃗n$ ) и не пронизывает его.

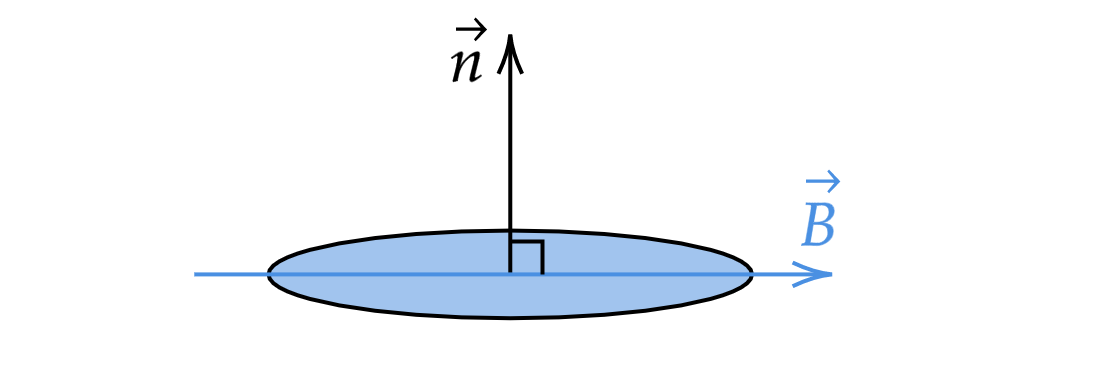
Физический смысл потока $Ф$ магнитной индукции заключается в том, что он показывает число линий индукции, пересекающих поверхность площадью $S$ (контур).

Электромагнитная индукция

Электромагнитная индукция (в широком смысле) — явление, при котором изменяющееся во времени магнитное поле порождает электрическое поле, а изменяющееся электрическое поле — магнитное поле.

Электромагнитная индукция (в узком смысле) — явление, при котором в электропроводящем контуре возникает индукционный ток при изменении магнитного потока, пронизывающего поверхность, ограниченную этим контуром.

Закон электромагнитной индукции (закон Фарадея)

Формулировка: ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную этим контуром.

|----------| |𝜀i = − ΔФ-| -------Δt--|

Данная формула справедлива, если магнитный поток меняется равномерно (линейно) с течением времени. В случае неравномерного изменения придется прибегнуть к помощи производных:

---------- |𝜀 = − Ф ′ --i-----t-

Закон Фарадея для катушки:

|------------| |𝜀i = − N ΔФ-| ---------Δt--|

При изменении магнитного потока возникает вихревое электрическое поле. ЭДС индукции показывает, какую работу совершает вихревое электрическое поле по перемещению единичного заряда по замкнутому контуру.

Движение проводника в магнитном поле

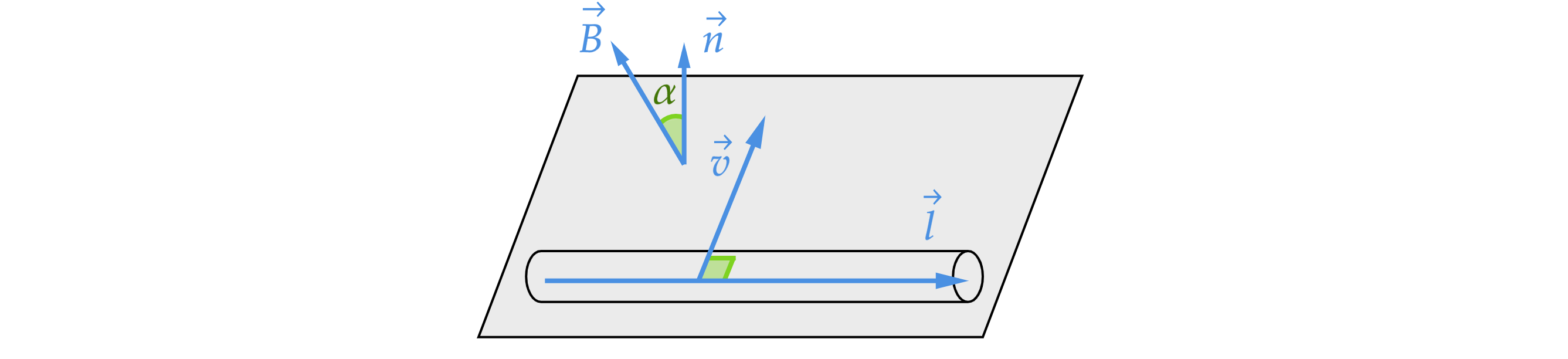
Закон Фарадея для движущегося проводника: при движении проводника в магнитном поле на его концах индуцируется разность потенциалов, пропорциональная скорости движения проводника.

|------------------| -Δ-φ =-U-=-Blv-cosα|

где $B$ — магнитная индукция поля, в котором движется проводник; $v$ и $l$ — скорость и длина проводника, соответственно; $α$ — угол между вектором $B$ и нормалью $⃗n$ к плоскости, в которой лежат векторы $⃗l$ и $⃗v$ .

Вывод закона Фарадея для движущегося проводника: способ 1

Пусть существует однородное магнитное поле $⃗B$ , в котором со скоростью $v$ движется проводник длиной $l$ .

В проводнике имеются свободные носители заряда (пусть положительные), которые движутся вместе с проводником со скоростью $v$ .

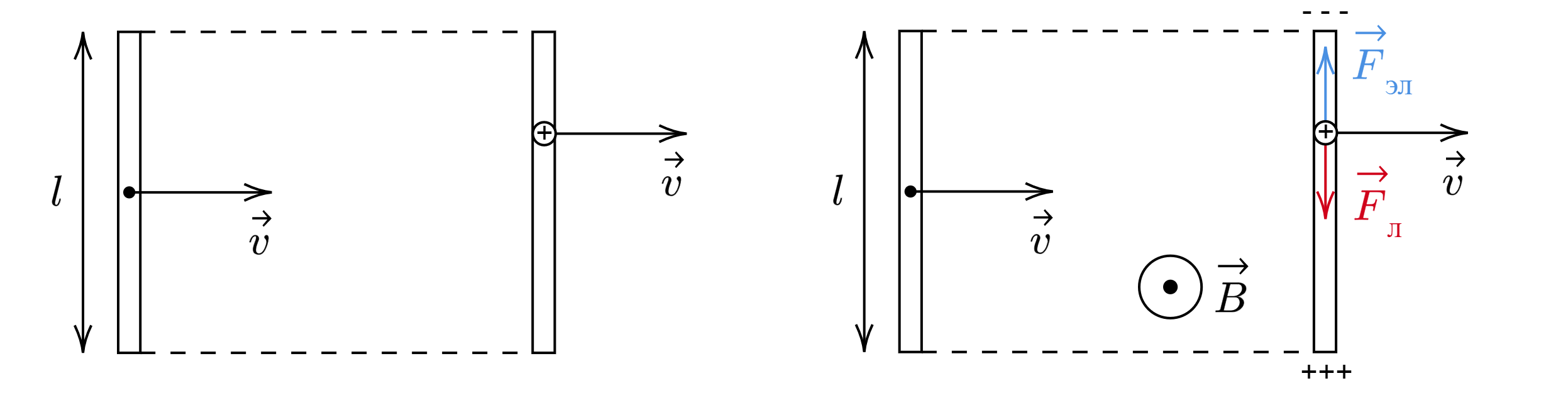
Когда положительно заряженная частица движется в магнитном поле со скоростью $v$ , на нее действует сила Лоренца. Направление силы Лоренца определяем по правилу левой руки — сила направлена вниз. Таким образом, при движении на одном конце проводника (куда направлена сила Лоренца) скапливаются положительные заряды, на другом — отрицательные. Эти заряды создают разность потенциалов и электрическое поле, в котором на положительно заряженную частицу действует электрическая сила, направленная от «плюса» к «минусу», то есть вверх.

Таким образом, положительно заряженные частицы перестанут перемещаться внутри проводника (в вертикальном направлении) в момент, когда сила электрическая сравняется с силой Лоренца: $Fэл = Fл$ .

Сила электрическая и сила Лоренца по определению:

qE = Bqv

С учетом связи напряжения и напряженности $U = Ed$ , где $d = l$ :

U- = Bv l

Таким образом, разность потенциалов, возникающая на концах проводника при движении проводника в однородном магнитном поле:

o |𝜀i| = u = Bvl (α = 90 )

Вывод закона Фарадея для движущегося проводника: способ 2

Теперь рассмотрим ту же ситуацию не на микроуровне, а на макроуровне. Перемещаясь, проводник «заметает» некоторый контур, площадь которого показана синим цветом на рисунке.

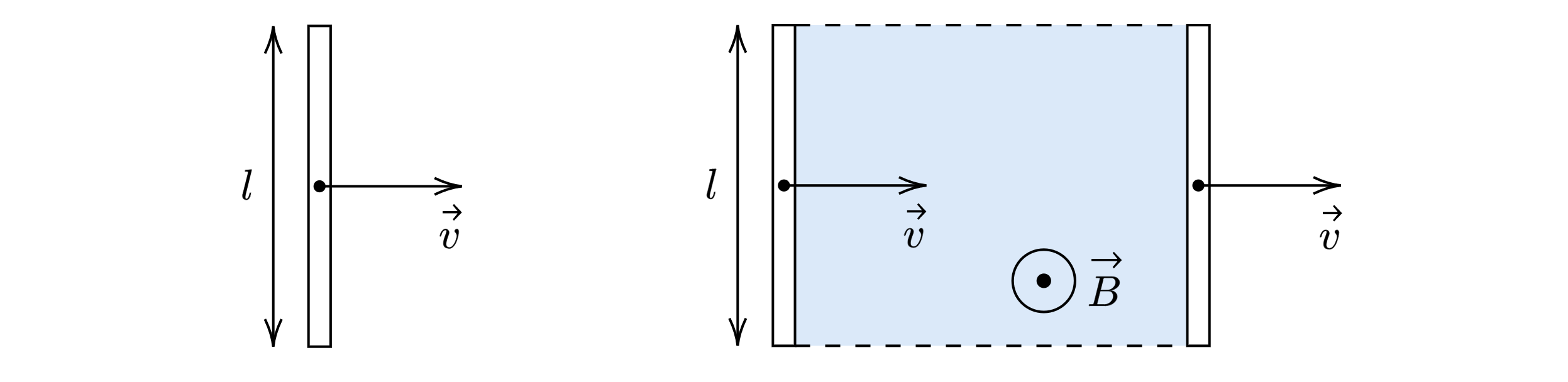
Модуль ЭДС самоиндукции при $α = 90o$ (рассматриваемый случай):

Δ Ф B |ΔS| |𝜀i| =----= ------ Δt Δt

Проводник проходит со скоростью $v$ за время $Δt$ расстояние $ΔS = vΔt$ :

|𝜀i| = Blv-Δt Δt

Отсюда ЭДС самоиндукции при движении проводника в однородном магнитном поле:

|𝜀| = Bvl i

Правило Ленца

Знак «минус» в формуле для закона электромагнитной индукции объясняется правилом Ленца.

Формулировка: индукционный ток имеет такое направление, при котором его собственное магнитное поле противодействует изменению магнитного потока, вызвавшему этот индукционный ток.

Рассмотрим, как работает данное правило, на примерах.

1) Пусть внешнее магнитное поле $B⃗внеш$ направлено «к нам» и оно увеличивается $ΔB внеш > 0$ .

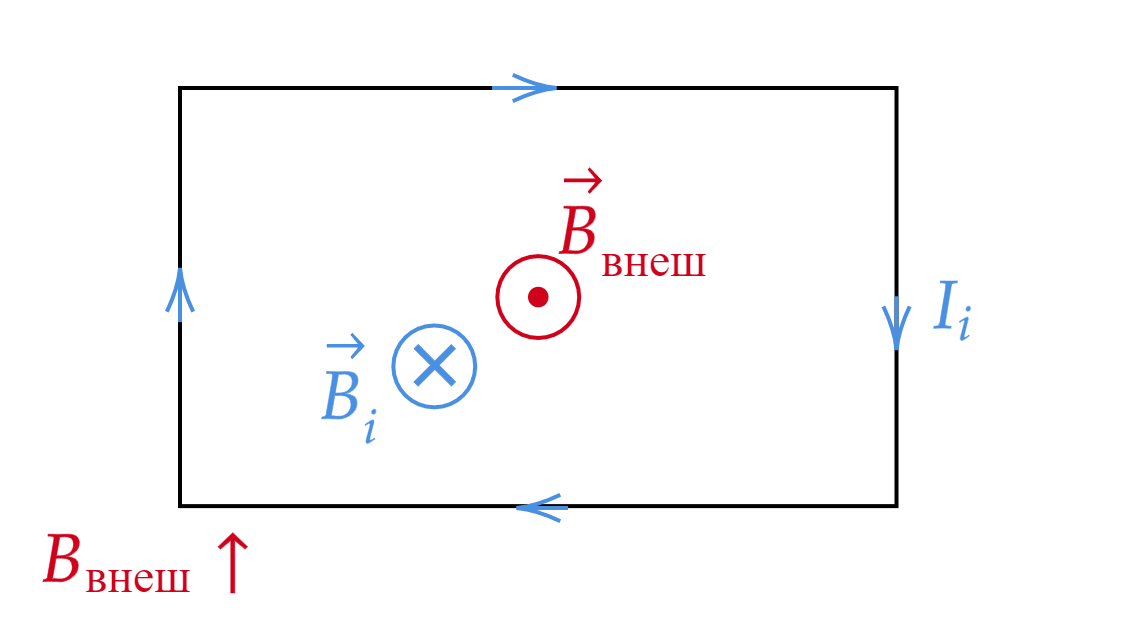
Магнитное поле увеличивается, следовательно, поток магнитной индукции положительный $Δ Ф > 0$ . Поскольку $Δ Ф > 0$ , то магнитный поток увеличивается, а это значит, что магнитное поле, создаваемое индукционным током, должно быть направлено противоположно внешнему полю $Bi ↑↓ Bвнеш$ . Таким образом, магнитное поле $⃗Bi$ , создаваемое индукционным током, направлено «от нас».

Проследим всю логическую цепочку. При изменении магнитной индукции $B$ изменяется и ее поток $Ф$ . При изменении потока электромагнитной индукции появляется ЭДС индукции $𝜀i$ . Раз в замкнутом контуре возникает ЭДС индукции, то по закону Ома для полной цепи возникает электрический ток (называемый в данном случае индукционным). Индукционный ток порождает свое поле, а именно индукционное поле $⃗ Bi$ . Это поле должно быть направлено противоположно внешнему $⃗ Bвнеш$ , чтобы препятствовать его изменению.

Определив направление индукционного поля $Bi$ , мы можем с помощью правила правой руки определить направление индукционного тока $I i$ .

2) Пусть внешнее магнитное поле $B⃗внеш$ направлено «к нам» и оно уменьшается $ΔB внеш < 0$ .

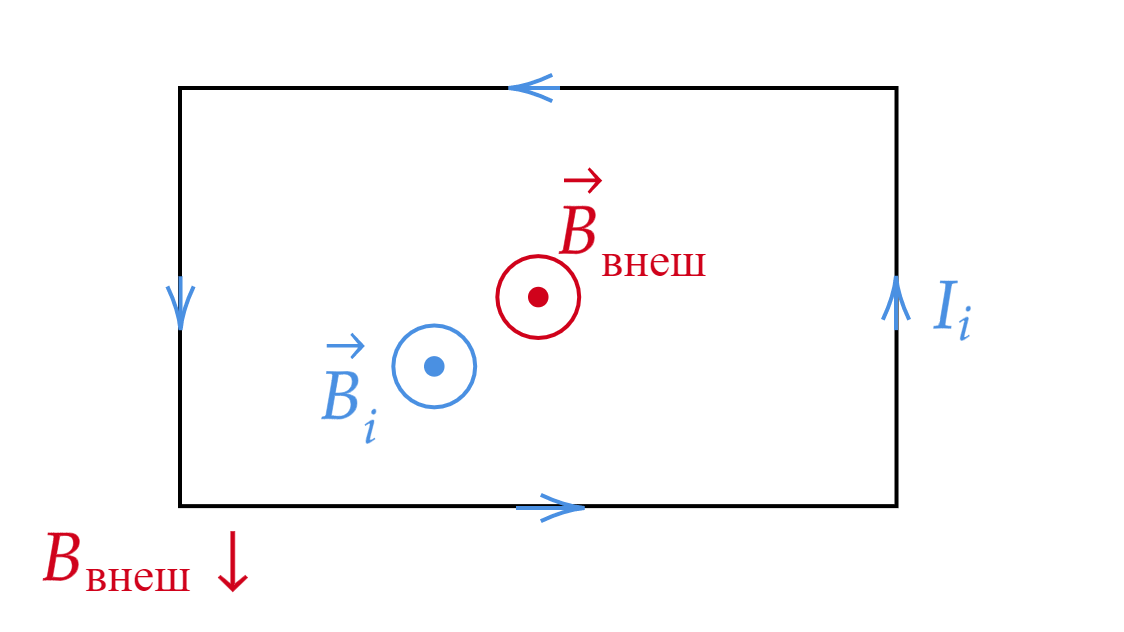
Магнитное поле уменьшается, следовательно, поток магнитной индукции отрицательный $Δ Ф < 0$ . Поскольку $Δ Ф < 0$ , то магнитный поток уменьшается, а это значит, что магнитное поле, создаваемое индукционным током, должно быть сонаправлено внешнему полю $Bi ↑↑ B внеш$ . Таким образом, магнитное поле $B⃗i$ , создаваемое индукционным током, направлено «к нам».

Вывод формулы для заряда

|ΔФ | |𝜀i| =-Δt-- (Δt → 0)

|𝜀i| = IiR

I = Δq- (Δt → 0) i Δt

Δq- |Δ-Ф-| Δt R = Δt

|------------| -|Δq-|R-=-|ΔФ-|-

Знак «минус» говорит о том, что ЭДС магнитной индукции действует против изменения. В задачах формата ЕГЭ, как правило, подразумевается использование модуля ЭДС магнитной индукции, поэтому знак «минус» перестает играть какую-либо роль. Но для понимания рассмотрим, почему формула «по-честному» выглядит именно так.

Пусть силовые линии магнитного поля пронизывают некоторый контур.

В качестве физико-математической базы для анализа возьмем следующие формулы:

ΔФ Ф = BS cosα (1) 𝜀i = −---- (2) Δt

Теперь рассмотрим несколько случаев.

1) Примем, что вектор нормали $⃗n$ сонаправлен с вектором $⃗B$ . Пусть магнитное поле усиливается $ΔB > 0$ .

В формуле (1) все величины, кроме магнитной индукции $B$ , постоянны. Так как вектор нормали $⃗n$ сонаправлен с вектором $⃗B$ , то поток магнитной индукции положительный $Ф > 0$ . Поскольку магнитное поле усиливается $ΔB > 0$ , то увеличивается и поток магнитной индукции $Δ Ф > 0$ .

Обратимся к формуле (2). Поскольку $Δ Ф > 0$ , то ЭДС магнитной индукции $𝜀i$ отрицательна.

Воспользуемся правилом правой руки: большой палец направлен по вектору нормали $⃗n$ , четыре пальца обхватывают контур и показывают положительное направление ЭДС магнитной индукции $𝜀i$ . Так как в нашем случае ЭДС магнитной индукции отрицательна, то она направлена в противоположную сторону. Изобразим это на рисунке ниже под пунктом 1).

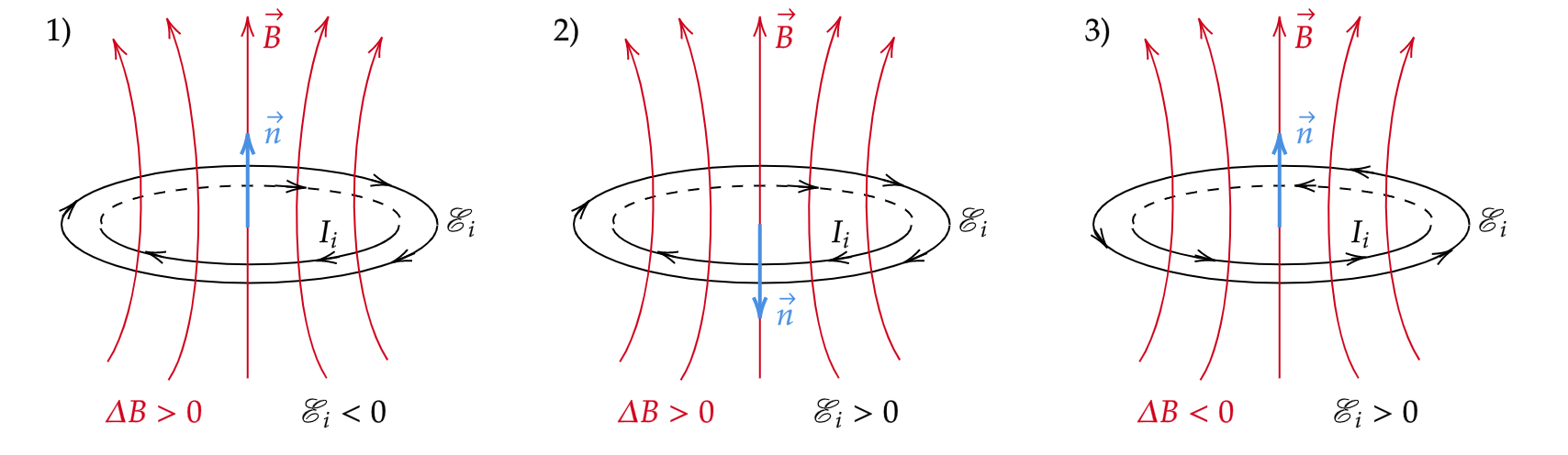
Внутри контура возникает электрическое поле, причем контур является замкнутым проводником. Так как имеется электрическое поле, замкнутая цепь и носители заряда, то возникает электрический ток, который называется индукционным. Индукционный ток порождается ЭДС магнитной индукции.

2) Примем, что вектор нормали $⃗n$ направлен противоположно вектору магнитной индукции $⃗B$ . Пусть магнитное поле усиливается $ΔB > 0$ .

Так как вектор нормали $⃗n$ противоположно направлен вектору $⃗ B$ , то поток магнитной индукции отрицательный $Ф < 0$ . Поскольку магнитное поле усиливается $ΔB > 0$ , то с учетом знака величина изменения потока магнитной индукции уменьшается $Δ Ф < 0$ .

По закону электромагнитной индукции ЭДС магнитной индукции положительна $𝜀i > 0$ («минус» от $Δ Ф$ на «минус» от самой формулы дает «плюс»). Воспользуемся правилом правой руки и определим, в какую сторону циркулирует электрический ток. Результат изобразим на рисунке под пунктом 2).

3) Примем, что вектор нормали $⃗n$ сонаправлен с вектором $⃗B$ . Пусть магнитное поле уменьшается $ΔB < 0$ .

Поскольку вектор $⃗n$ сонаправлен с вектором $⃗B$ , то поток магнитной индукции $Ф$ положительный $Ф > 0$ . Так как магнитное поле уменьшается $ΔB < 0$ , то магнитный поток уменьшается $Δ Ф < 0$ .

Предыдущая справка

Следующая справка