Молекулярно-кинетическая теория. Газовые законы

Основные положения молекулярно-кинетической теории

1) Любое вещество состоит из мельчайших частиц — молекул и атомов. Они расположены в пространстве дискретно, то есть на некоторых расстояниях друг от друга.

2) Атомы или молекулы вещества находятся в состоянии беспорядочного движения, которое никогда не прекращается.

3) Атомы или молекулы вещества взаимодействуют друг с другом силами притяжения и отталкивания, которые зависят от расстояний между частицами.

Идеальный газ

Идеальный газ — это газ, частицы которого являются не взаимодействующими на расстоянии материальными точками и испытывают абсолютно упругие соударения друг с другом и со стенками сосуда.

Основное уравнение МКТ

Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Из-за соударений молекулы оказывают давление на стенки.

Основное уравнение МКТ идеального газа:

где — давление, — масса одной молекулы, — концентрация, — средняя квадратичная скорость.

Единицы измерения:

Па — паскаль.

Средняя квадратичная скорость:

Концентрация:

где N — число молекул в объеме V.

Вывод основного уравнения МКТ

В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.

Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция скорости, параллельная стенке, остается неизменной (см. рисунок).

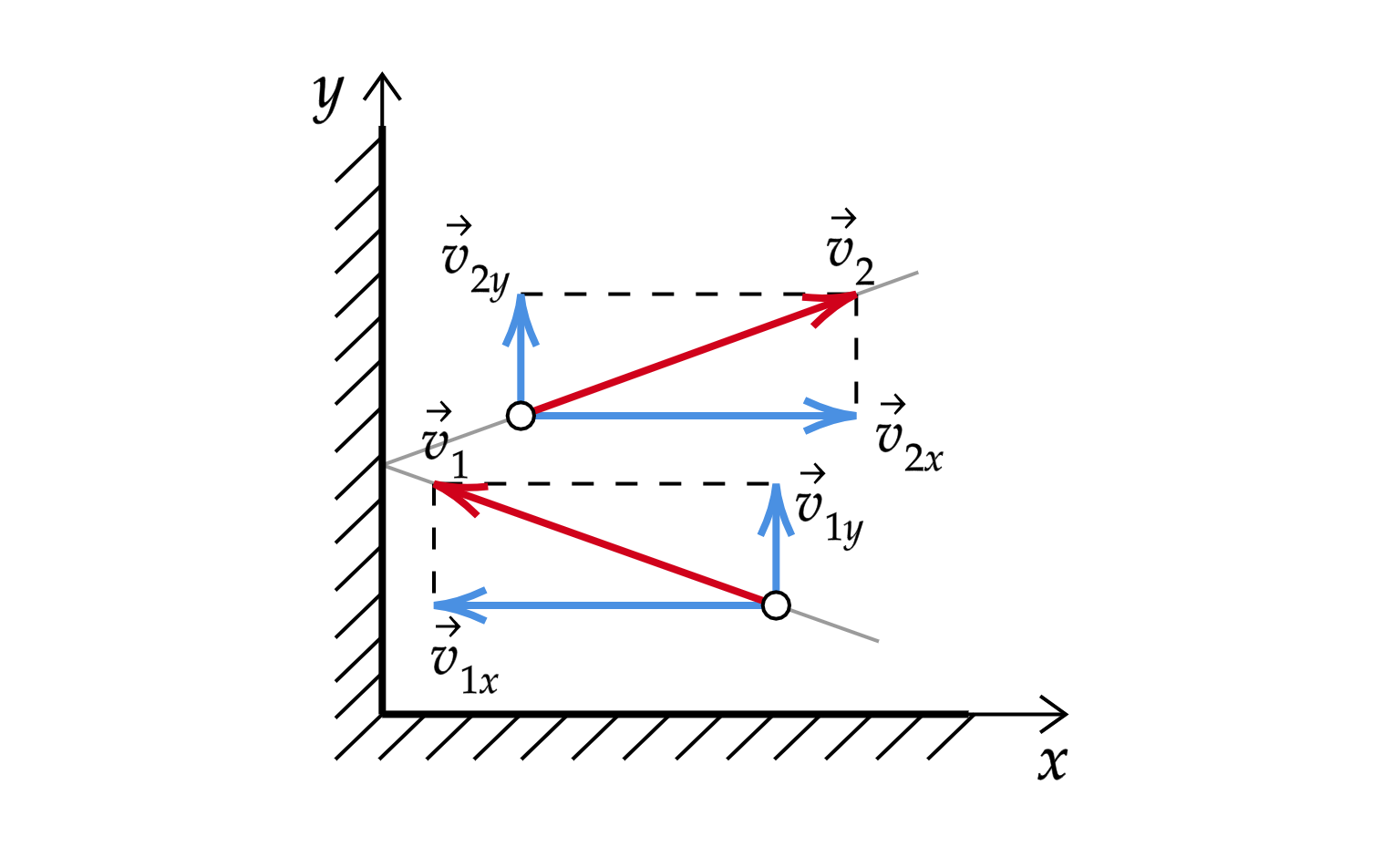
Поэтому изменение импульса молекулы будет равно , где — масса молекулы.

Выделим на стенке некоторую площадку (см. рисунок). За время с этой площадкой столкнутся все молекулы, имеющие проекцию скорости , направленную в сторону стенки, и находящиеся в цилиндре с основанием площади и высотой .

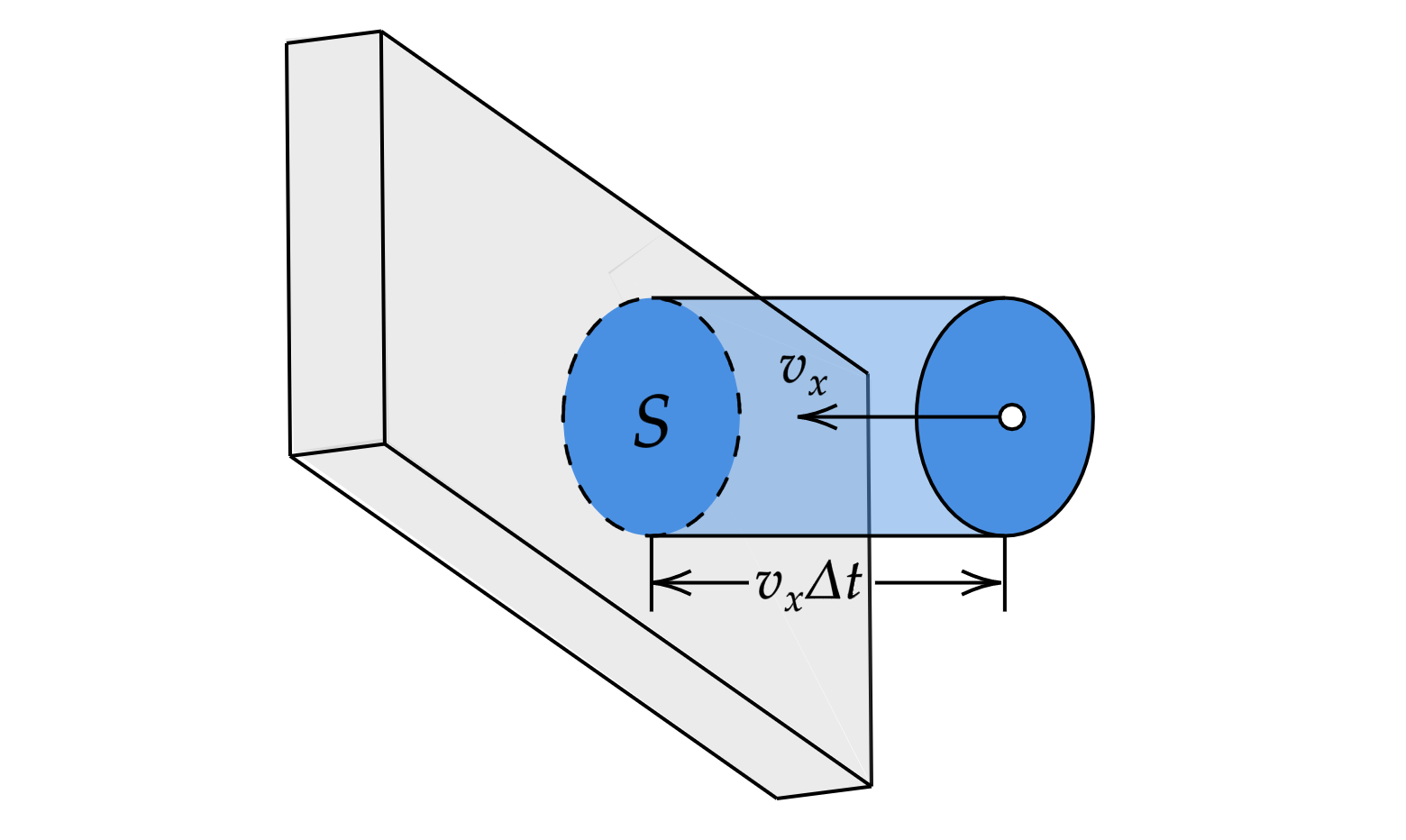
Пусть в единице объема сосуда содержатся молекул; тогда число молекул в объеме цилиндра равно . Но из этого числа лишь половина движется в сторону стенки, а другая половина движется в противоположном направлении и со стенкой не сталкивается. Следовательно, число ударов молекул о площадку за время равно .

Поскольку каждая молекула при столкновении со стенкой изменяет свой импульс на величину , то полное изменение импульса всех молекул, столкнувшихся за время с площадкой , равно .

По законам механики это изменение импульса всех столкнувшихся со стенкой молекул происходит под действием импульса силы , где — некоторая средняя сила, действующая на молекулы со стороны стенки на площадке . Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку . Поэтому можно записать:

Разделив обе части на , получим:

где — давление газа на стенку сосуда.

При выводе этого соотношения предполагалось, что все молекул, содержащихся в единице объема газа, имеют одинаковые проекции скоростей на ось X. На самом деле это не так.

В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными, а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям.

Теперь формулу для давления газа можно записать в виде

Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов их проекций на координатные оси равны между собой:

Последнее равенство вытекает из формулы:

Формула для среднего давления газа на стенку сосуда запишется в виде

где — средняя кинетическая энергия молекул — среднее арифметическое их кинетических энергий.

Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

Кинетическая энергия

МКТ рассматривает тепловое движение — движение, при котором молекулы хаотично двигаются. Молекулы при хаотичном движении имеют некоторую скорость и обладают кинетической энергией. Кинетическая энергия теплового (хаотического) движения характеризует температуру тела. Температура тела показывает, насколько быстро двигаются молекулы.

Кинетическая энергия поступательного движения одной молекулы:

где — постоянная Больцмана, — абсолютная температура.

Данная формула показывает, что температура тела является характеристикой кинетической энергии поступательного движения каждой молекулы в отдельности.

Средняя квадратичная скорость

Кинетическая энергия движения одной молекулы по определению:

Приравняем данное выражение к предыдущему:

Средняя квадратичная скорость движения одной молекулы:

Варианты основного уравнения МКТ

1. Выведенное ранее основное уравнение МКТ имеет вид:

2. Домножим и поделим уравнение под номером 1 на 2:

3. Подставим в уравнение под номером 2 выражение для кинетической энергии:

Температурная шкала Кельвина

В МКТ для температур принято использовать абсолютную шкалу Кельвина.

Единицы измерения:

К — кельвин.

Перевод из шкалы Цельсия в шкалу Кельвина:

где — температура в градусах Цельсия.

У шкалы Кельвина существует абсолютный ноль, ниже которого ничего нет:

В классической физике принято считать, что при температуре 0 кельвинов молекулы перестают двигаться и тепловое движение прекращается.

Количество вещества

Работать с массами молекул зачастую неудобно. В связи с этим вводится понятие количества вещества .

Единицы измерения:

— моль.

1 моль — это молекулярная «упаковка», содержащая определенное количество молекул. Моль любого вещества содержит одно и то же число молекул — число Авогадро.

Количество вещества можно найти по формулам:

где — количество молекул (в штуках), — масса вещества, — молярная масса вещества.

Молярная масса

Молярная масса — масса одного моля вещества, или масса одной «упаковки» молекул.

Единицы измерения:

кг/моль.

Молярную массу можно найти, используя таблицу Менделеева.

Например, молекула воды содержит два атома водорода и один атом кислорода и имеет химическую формулу . Атомная масса водорода из таблицы Менделеева 1, атомная масса кислорода 16, причем атом водорода «повторяется» в молекуле 2 раза, а атом кислорода — один раз. Исходя из этого, найдем молярную массу молекулы воды: 18 г/моль. В системе СИ: кг/моль.

Уравнение состояния идеального газа

Уравнение Клапейрона-Менделеева, или уравнение состояния идеального газа, связывает три макроскопических параметра газа.

где — давление газа, — его объем, — количество вещества ( — масса газа, — его молярная масса), — абсолютная температура газа, — универсальная газовая постоянная.

Уравнение Клапейрона-Менделеева также можно записать в виде

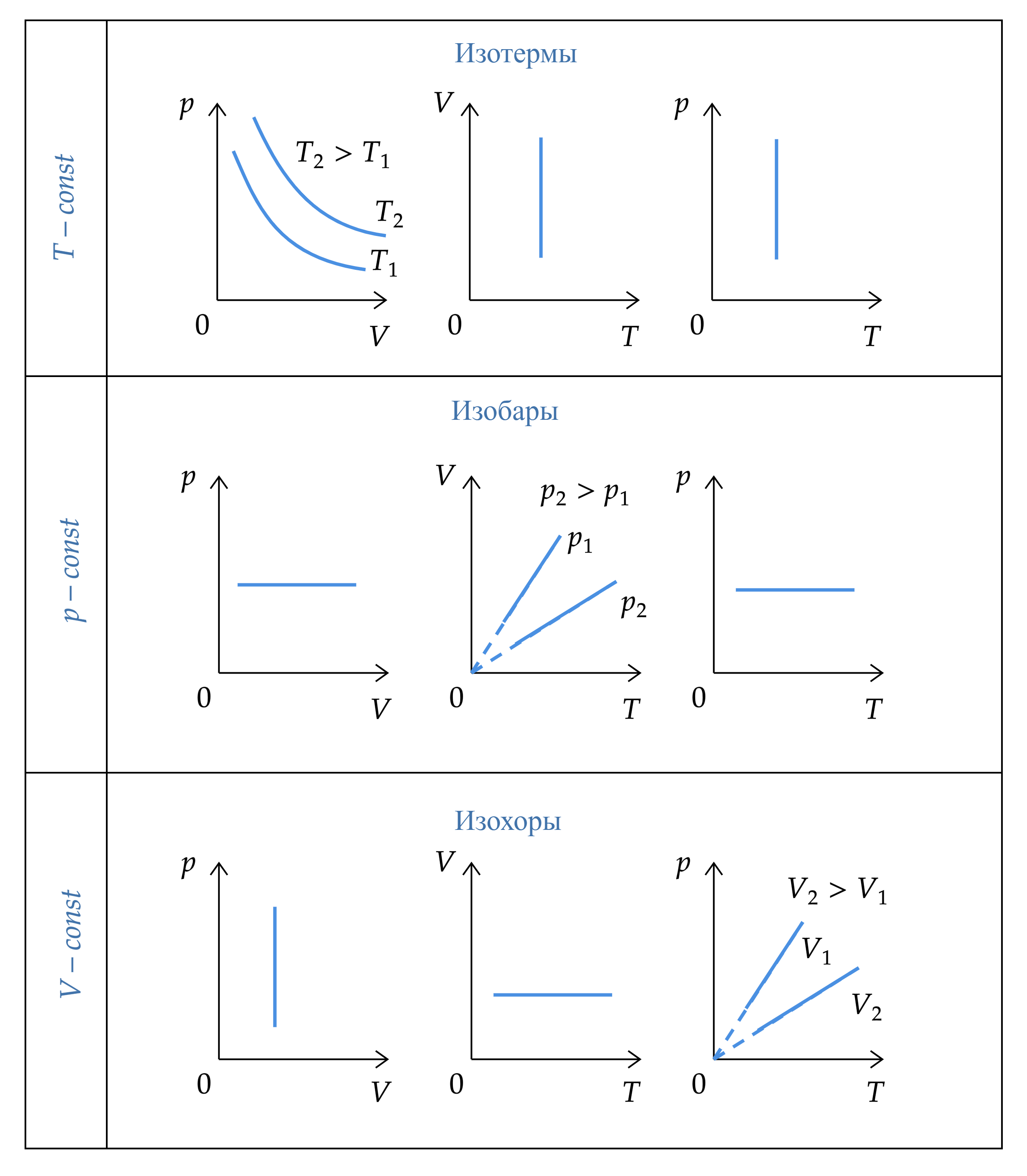
Изопроцессы

Изопроцессы — термодинамические процессы, во время которых количество вещества газа и один из параметров состояния: давление, объём или температура — остаётся неизменным.

• Изотермический процесс

  — по закону Бойля-Мариотта

  

• Изохорный процесс

  — по закону Шарля

  

• Изобарный процесс

  — по закону Гей-Люссака

  

Графики изопроцессов