Электричество и магнетизм

Магнетизм

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Электричество и магнетизм

Теоретическая справка

#976

Магнитное поле

Для магнитного поля определения как такового не существует. Но у магнитного поля есть свойства:
- магнитное поле материально и существует независимо от нас и наших знаний о нем;
- существует два типа магнитных полюсов — северный и южный (принято условно);
- полюса всегда два (невозможно создать магнит, у которого был бы только один полюс);
- магнитное поле взаимодействует с движущимися зарядами: если заряд один — силой Лоренца, если проводник с током — силой Ампера;
- cиловые линии магнитного поля всегда замкнуты и не имеют ни начала, ни конца.

Источники магнитного поля:

1) движущиеся заряженные частицы (положительные и отрицательные);

2) проводник с током (т.к. ток — это упорядоченное движение заряженных частиц);

3) постоянный магнит.

Индикаторы магнитного поля (то, что взаимодействует с магнитным полем):

1) движущиеся заряженные частицы (положительные и отрицательные);

2) проводник с током;

3) постоянный магнит.

Каждый из этих объектов создает вокруг себя магнитное поле, и эти магнитные поля взаимодействуют друг с другом.

Силовые линии магнитного поля

Силовые линии — это графическая визуализация силового поля.

Рассмотрим постоянный магнит, у которого $N$ — северный полюс, $S$ — южный.

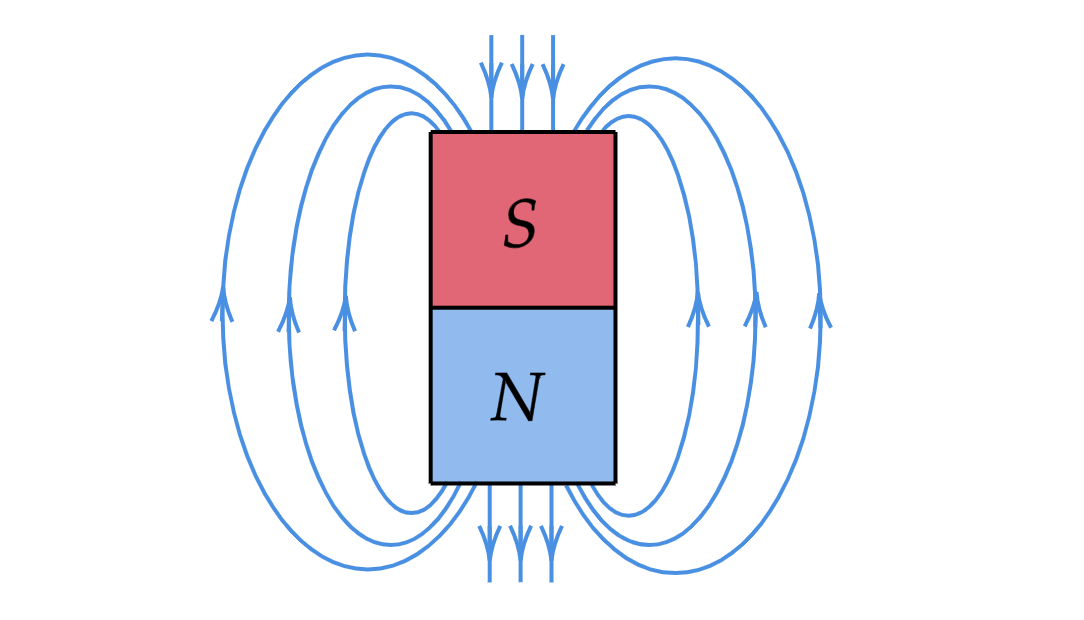
Свойства силовых линий магнитного поля:
- Силовые линии заполняют пространство таким образом, что касательные к ним в каждой точке пространства совпадают по направлению с вектором магнитной индукции.
- Силовые линии магнитного поля всегда начинаются на «севере» и заканчиваются на «юге» вне постоянного магнита и идут от «юга» к «северу» внутри него.
- В отличие от силовых линий электростатического поля, силовые линии магнитного поля всегда замкнуты (магнитное поле является полем вихревого типа).
- Через каждую точку проходит только одна силовая линия магнитного поля (то есть они не пересекаются).

Проводник с током

1. Правило буравчика (винта):

Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.

2.1 Правило правой руки:

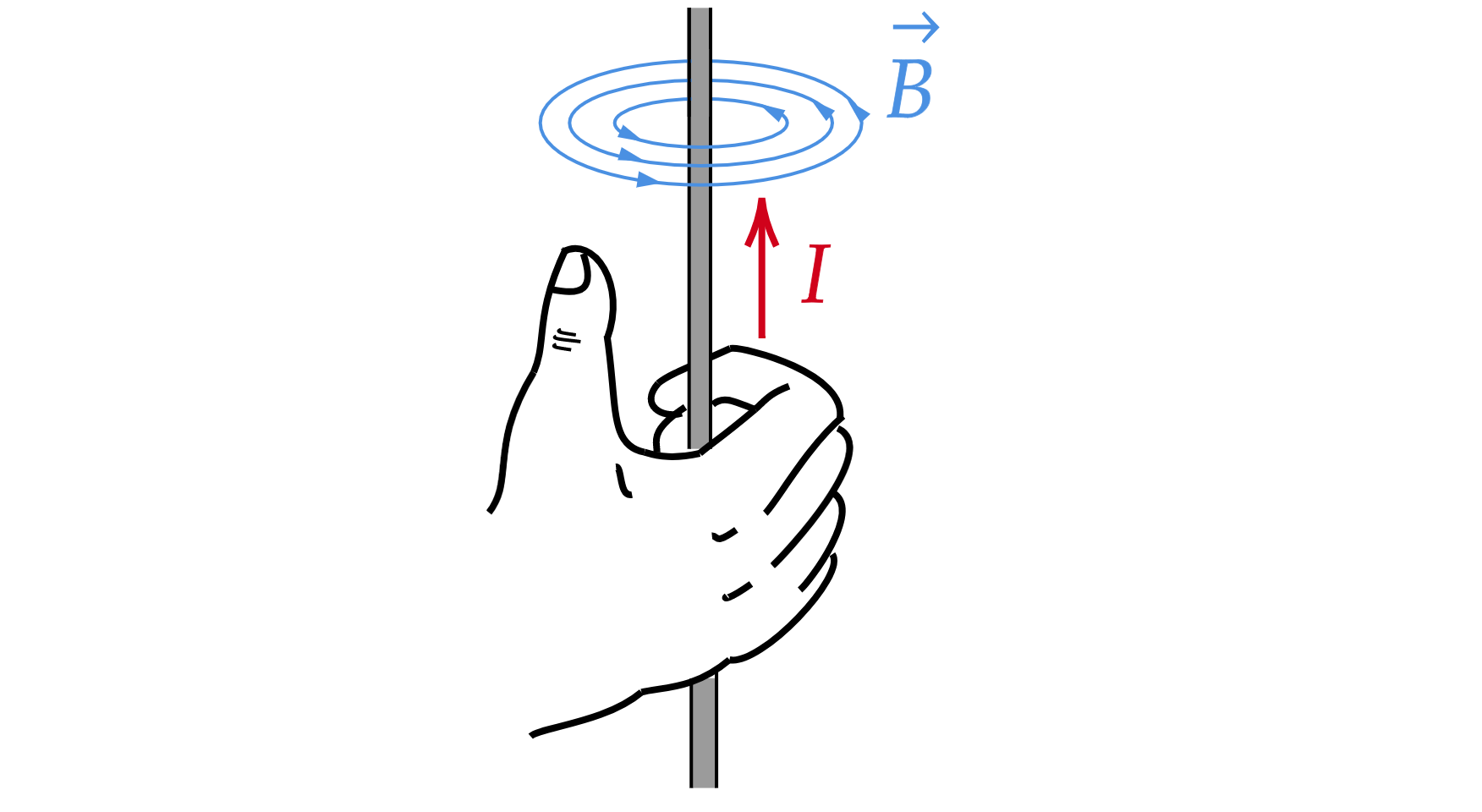
Если обхватить проводник правой рукой так, чтобы отставленный на 90 градусов большой палец указывал направление тока, то остальные пальцы покажут направление огибающих проводник линий магнитной индукции поля, создаваемого этим током. А значит, мы определим и направление вектора магнитной индукции, направленного везде по касательной к этим линиям.

2.2 Правило правой руки для замкнутого проводника с током:

Если обхватить правой рукой контур, то отогнутый на 90 градусов большой палец покажет направление вектора магнитной индукции.

Вектор магнитной индукции

Магнитная индукция — силовая характеристика магнитного поля.

Обозначение и единицы измерения: $[B ] =$ Тл — тесла.

Является векторной физической величиной.

Силы в магнитном поле

1. Сила Ампера

Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.

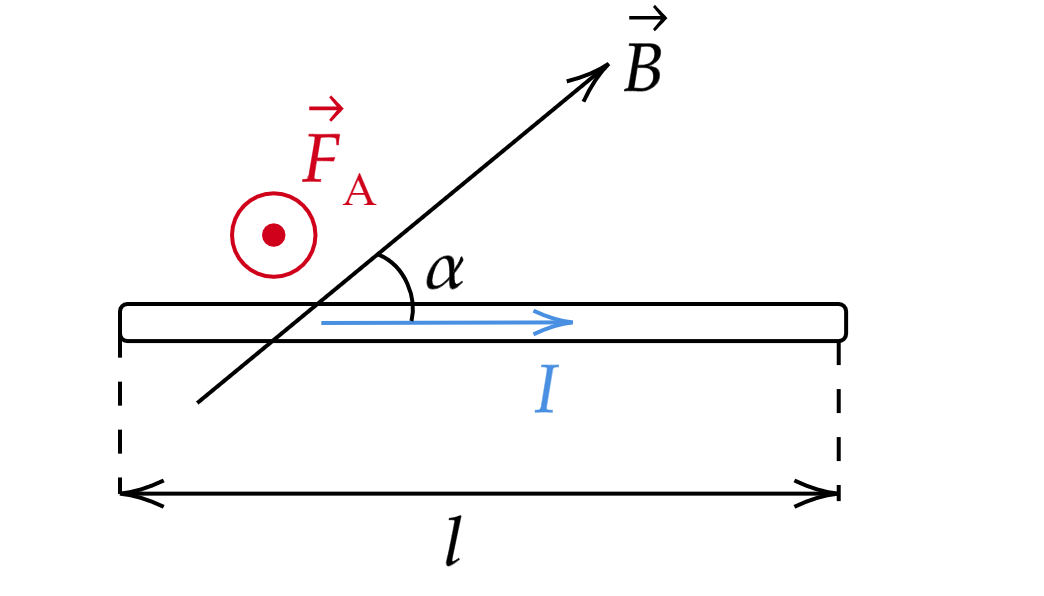
Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:

|------------| F-А =-BIl-sinα-

где $B$ — модуль вектора магнитной индукции, $I$ — сила тока, $sinα$ — синус угла между вектором индукции магнитного поля и проводником.

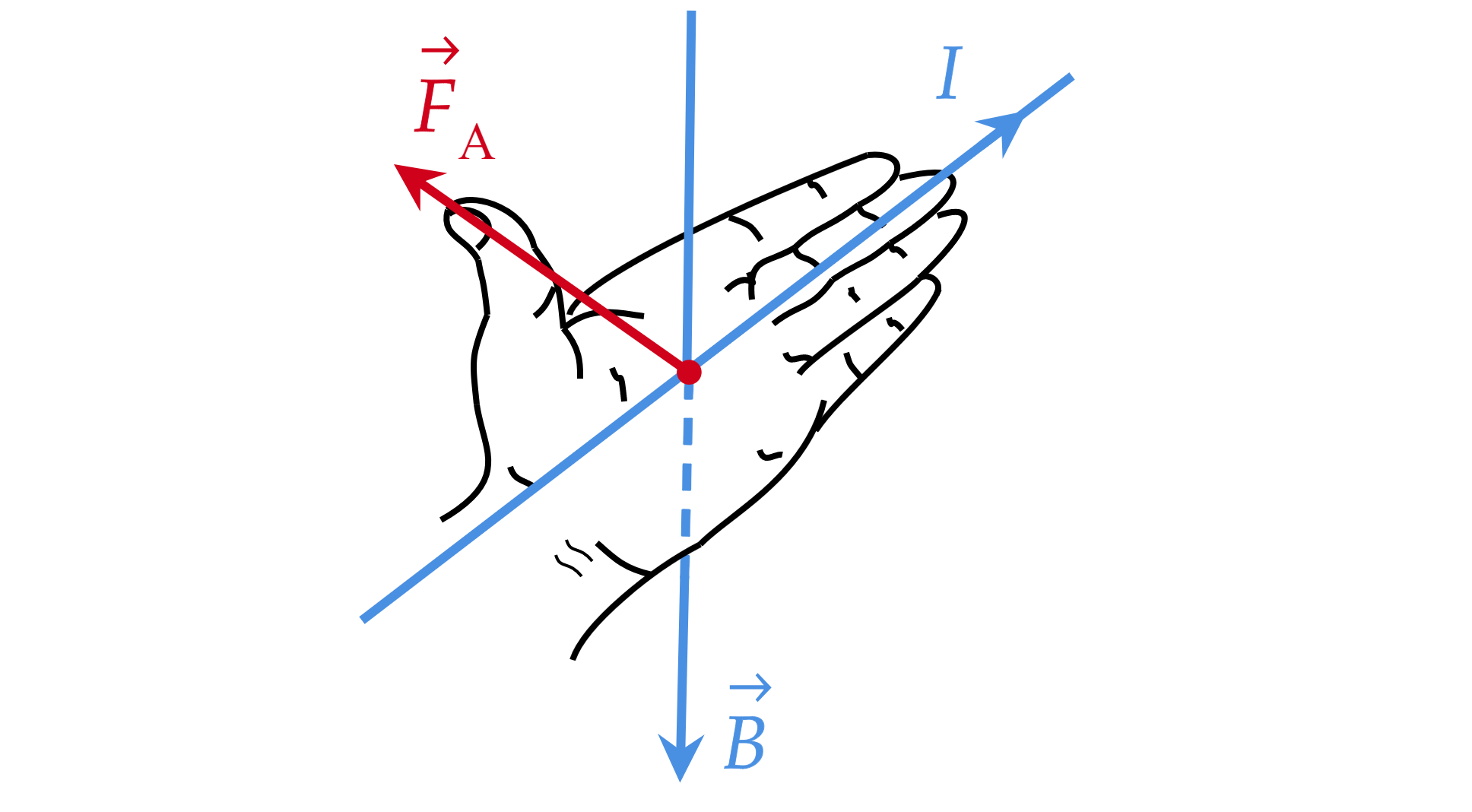
Правило левой руки (для силы Ампера)

Если расположить левую руку так, чтобы магнитные линии пронизывали ладонь, а вытянутые четыре пальца указывали направление тока в проводнике, то отогнутый большой палец укажет направление силы Ампера.

2. Сила Лоренца

Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца:

|------------| FЛ = qvB sin α| --------------

где $q$ — заряд частицы, $v$ — скорость молекул в проводнике.

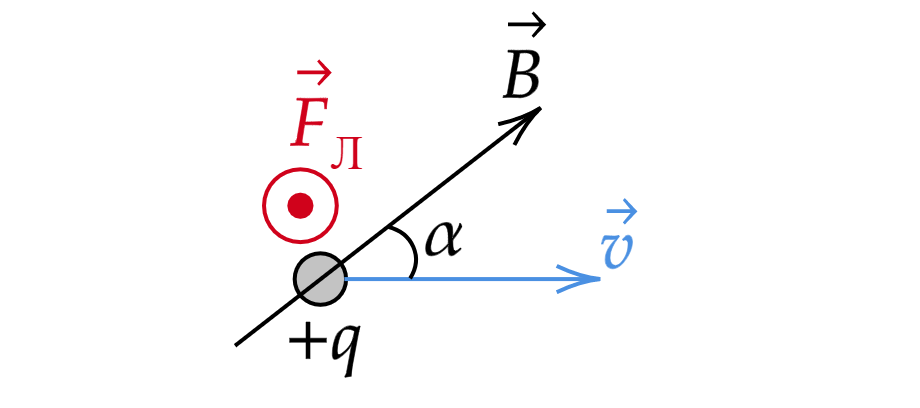
Сила Лоренца $F⃗Л$ всегда перпендикулярна вектору скорости $⃗v$ и вектору магнитной индукции $B⃗$ .

Правило левой руки (для силы Лоренца)

Если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца $F Л$ .

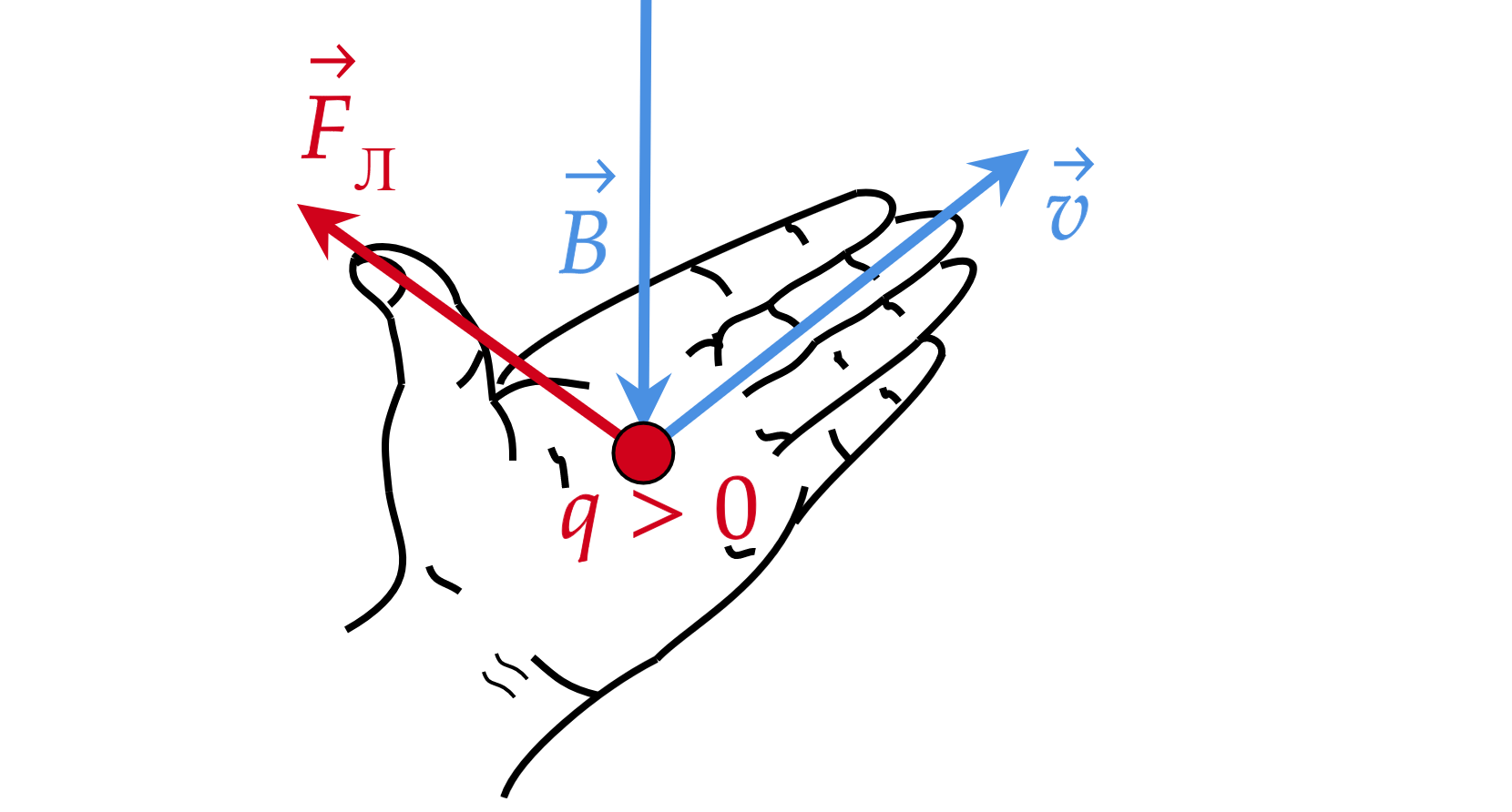
Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону.

Траектория заряженной частицы в электростатическом поле

1) $⃗ ⃗v || E$

Если частица влетает параллельно вектору напряженности $⃗E$ , то она будет двигаться равноускоренно по прямой.

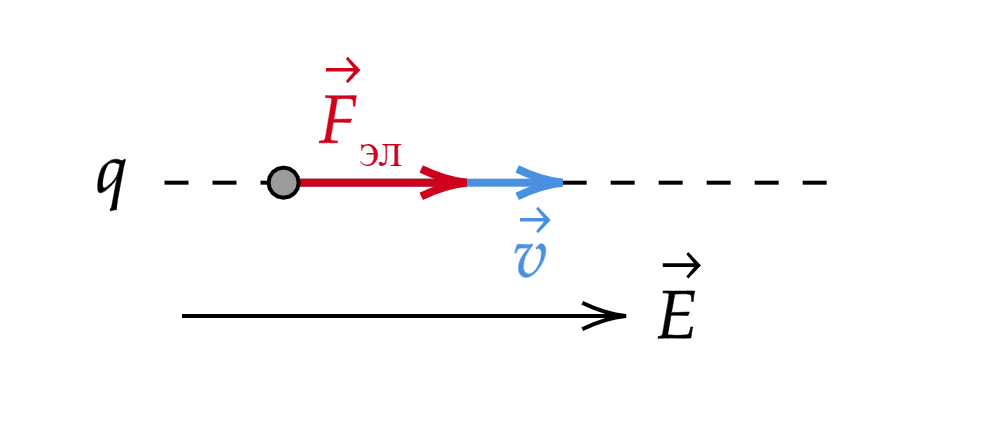
Из второго закона Ньютона $⃗Fэл = m⃗a$ и силу электрическую можно определить как $⃗Fэл = q⃗E$ . Учитывая, что $⃗v ||E⃗$ , можно сделать вывод:

⃗a ||⃗v

2) $⃗v || ⃗E$

Если частица влетает под углом к вектору напряженности $⃗ E$ , то она будет двигаться равноускоренно по параболе.

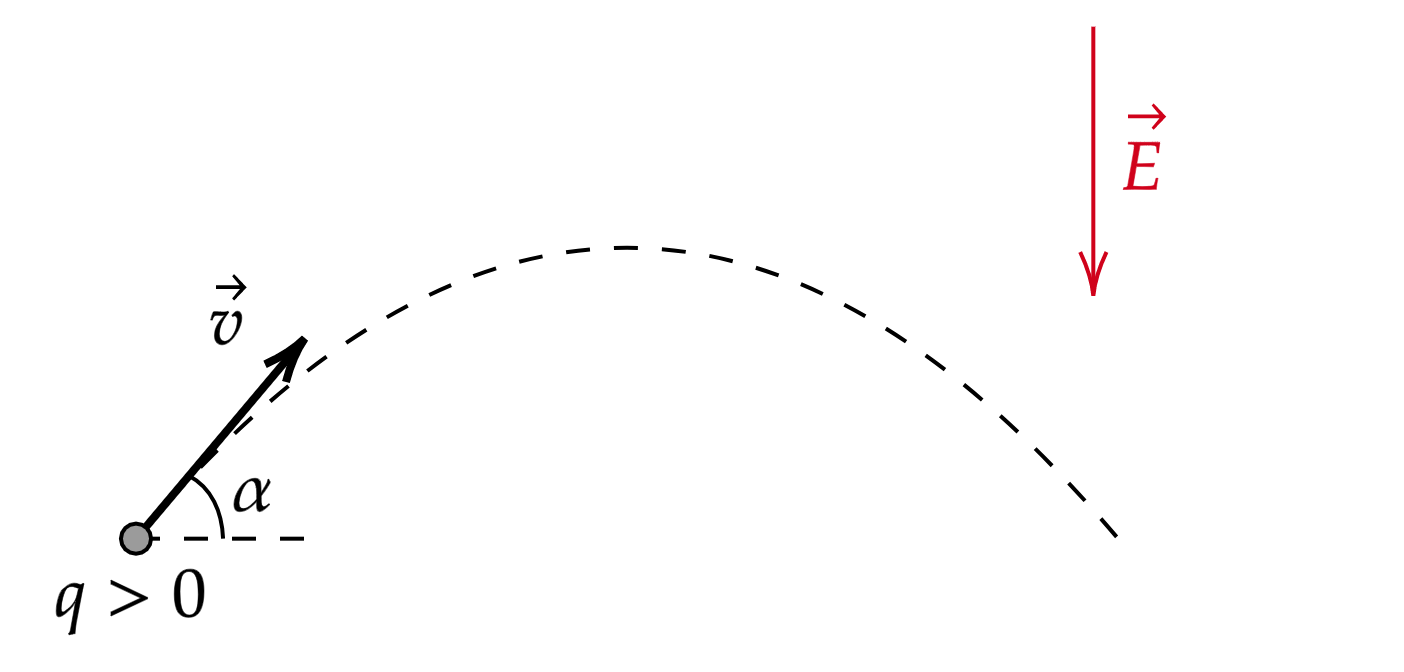
К этому выводу можно прийти, исходя из тех же рассуждений, что были проделаны в пункте 1). Из второго закона Ньютона $⃗F = m ⃗a эл$ и силу электрическую можно определить как $⃗F = qE⃗ эл$ . Учитывая, что $⃗v не ||E⃗$ , можно сделать вывод:

⃗a не ||⃗v

Траектория заряженной частицы в магнитном поле

1) $⃗ ⃗v || B$

Если частица влетает параллельно вектору магнитной индукции $⃗B$ , то она будет двигаться равномерно по прямой.

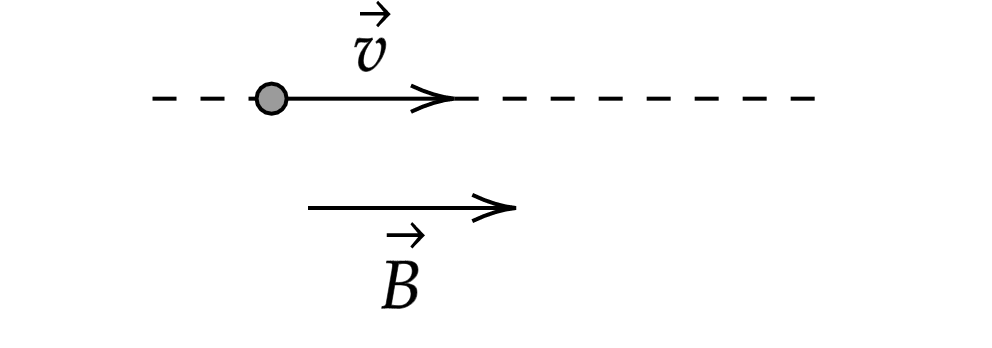
На частицу в магнитном поле действует сила Лоренца:

FЛ = Bvq sin α

Так как $⃗B ||⃗v$ , то угол $α$ равен нулю, следовательно, $sin α$ также равен нулю. Отсюда и сила Лоренца равна нулю, поэтому магнитное поле «не ощущает» влетевшую частицу.

2) $⃗ ⃗v ⊥ B$

Если частица влетает перпендикулярно вектору магнитной индукции $⃗B$ , то она будет двигаться равномерно по окружности.

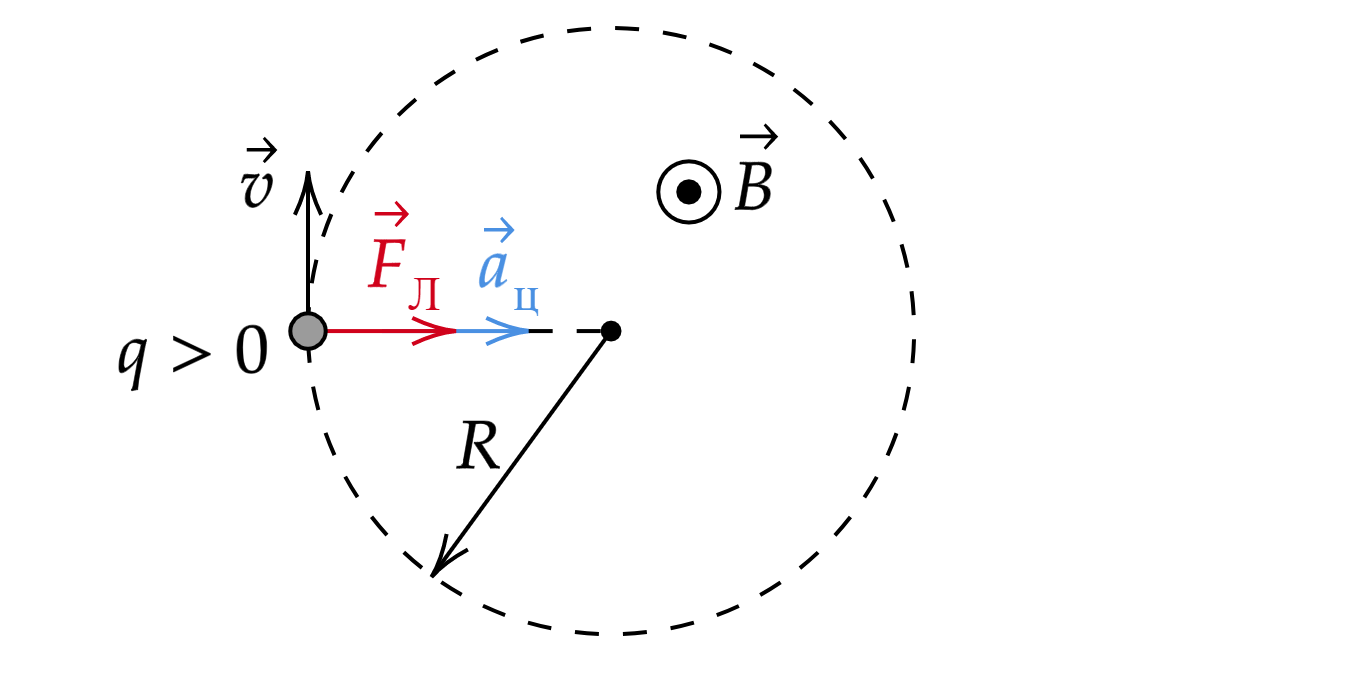
На частицу в магнитном поле действует сила Лоренца:

FЛ = Bvq sin α

По второму закону Ньютона:

FЛ = ma ц

Центростремительное ускорение можно найти по формуле:

v2 aц = R

Подставим эти выражения друг в друга поочередно:

Bvq = mv2 R

Сократим скорости:

v- Bq = m R

Найдем период обращения:

2πR 2πm T = ---- = ---- v Bq

Можно сделать вывод, что в данном случае период обращения частицы не зависит от ее скорости.

Приведенные выше выкладки часто встречаются в задачах по магнетизму. Обратите внимание, что в случае, если данная формула необходима для решения задач второй части, то обязательно нужно дать ее вывод.

3) $⃗v$ под углом к $B⃗$

Если частица влетает под углом к вектору магнитной индукции $B⃗$ , то она будет двигаться по спирали.

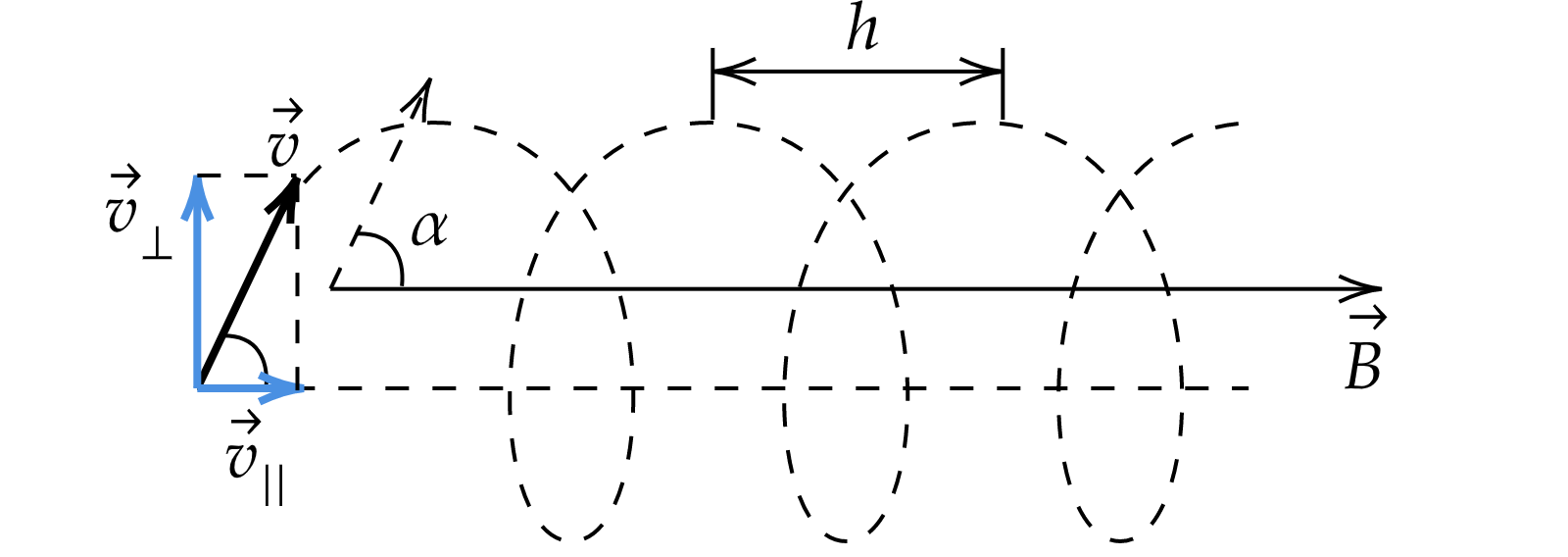
Разложим скорость $⃗v$ на две составляющие:

⃗v = ⃗v|| + ⃗v⊥

Скорость параллельная $⃗v ||$ не изменяется, скорость перпендикулярная $⃗v ⊥$ вращает частицу по окружности.

При сложении этих скоростей, результирующая скорость $⃗v$ закручивает частицу по спирали.

Вспомним выкладки из пункта 2), откуда мы вывели

v Bq = m R-

В данном случае радиус спирали и период обращения частицы по спирали:

R = mv-⊥ T = 2πm- qB qB

Шаг спирали:

2πm- h = v||T = v||qB

Причем $v|| = vcosα$ и $v⊥ = vsin α$ .

Математический аппарат: векторное произведение векторов

Векторным произведением двух векторов $⃗a$ и $⃗ b$ называется такой третий вектор $⃗c$ , который удовлетворяет следующим трем условиям:

1) вектор $⃗c$ перпендикулярен векторам $⃗a$ и $⃗b$ ;

2) модуль вектора $⃗c$ равен $⃗ ⃗ |⃗c| = |⃗a|⋅|b|⋅sin(⃗a,b)$ ;

3) векторы $⃗a$ , $⃗b$ , $⃗c$ образуют правую тройку.

Обозначение векторного произведения векторов $⃗a$ и $⃗b$ : $⃗c = ⃗a ×⃗b = [⃗a,⃗b]$

Это строгое определение. Теперь разберем все по пунктам.

Итак, все действие происходит в пространстве. Пусть нам нужно векторно умножить вектор $⃗a$ на вектор $⃗b$ , которые в своей плоскости (на рис. показана синим цветом) раздвинуты на угол $α$ .

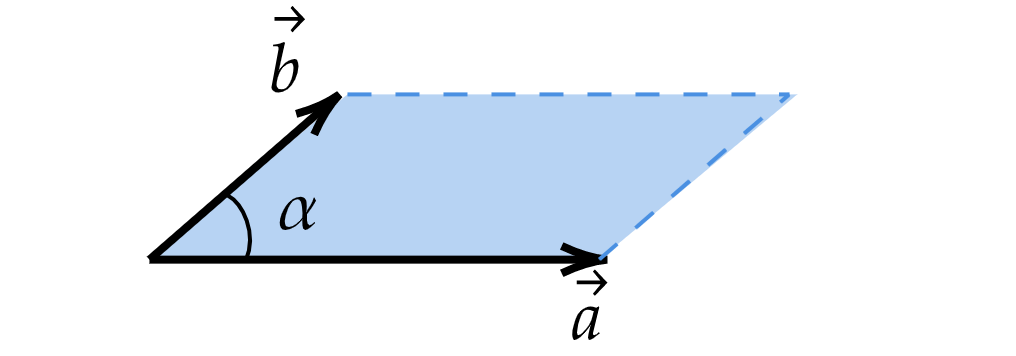
Из строгого определения векторного произведения векторов мы знаем, что в результате должен получиться другой вектор, назовем его $⃗c$ .

Любой вектор определяется двумя характеристиками — направлением и модулем. То есть, чтобы определить вектор $⃗c$ в пространстве, необходимо знать, куда он направлен и какова его длина.

С длиной все просто. Из определения модуль вектора, полученного в результате векторного произведения, равен $⃗ |⃗c| = |⃗a|⋅|b|⋅sinα$ (пункт 2).

Теперь разберемся с направлением вектора $⃗c$ . Из определения вектор $⃗c$ , полученный в результате векторного произведения $⃗a$ на $⃗b$ , должен быть перпендикулярен этим векторам (пункт 1). То есть нам нужно представить такой вектор, который был бы перпендикулярен синей плоскости. Вектор может быть направлен либо вверх, либо вниз относительно плоскости, при этом быть ей перпендикулярным.

Чтобы определить, вверх или вниз направлен вектор, возьмем ладонь правой руки и четырьмя вытянутыми пальцами постараемся «закрутить» наименьший угол от вектора $⃗a$ к вектору $⃗b$ , причем большой палец отставим на 90 градусов (он и покажет направление вектора $⃗c$ ).

Есть два варианта, как мы можем «закрутить» угол от вектора $⃗a$ к вектору $⃗b$ .

Очевидно, что угол $α$ явно меньше угла $β$ , и поэтому именно он нам подходит. Когда мы «закручивали» вектор $⃗a$ к вектору $⃗b$ через угол $α$ , большой палец правой руки показывал вверх. Таким образом, мы определили направление вектора $⃗c$ и можем изобразить его на рисунке:

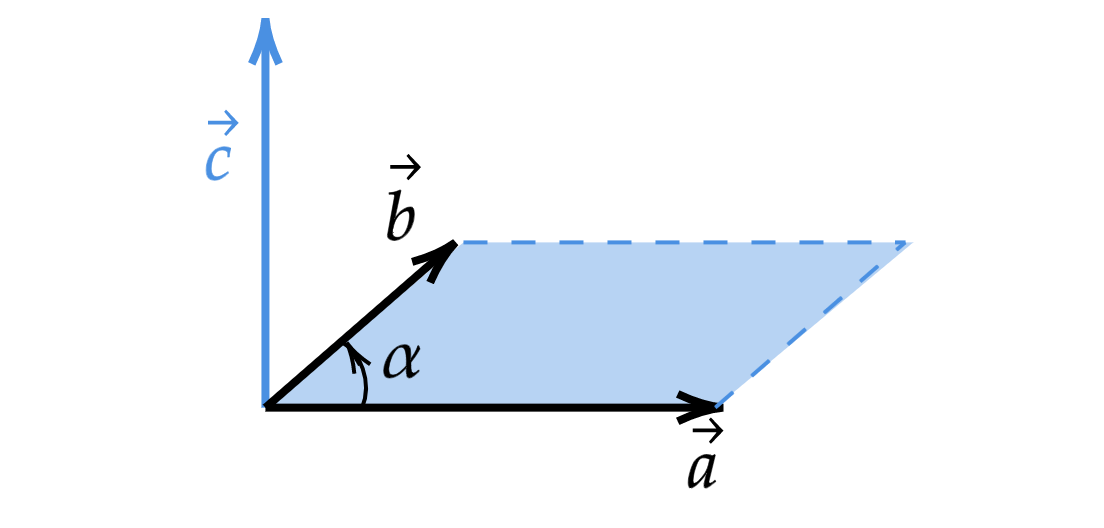
Теперь векторно умножим вектор $⃗b$ на вектор $⃗a$ . По модулю вектор $⃗d$ , который получится в результате векторного умножения $⃗b$ на $⃗a$ , будет равен модулю вектора $⃗c$ , который получился в результате векторного умножения $⃗a$ на $⃗b$ . Однако направление векторов $⃗c$ и $⃗d$ будет разным. При векторном умножении вектора $⃗b$ на вектор $⃗a$ нам нужно «закрутить» четырьмя вытянутыми пальцами правой руки наименьший угол уже от вектора $⃗b$ к вектору $⃗a$ . Наименьшим углом в данном случае по-прежнему является угол $α$ , однако отставленный на 90 градусов большой палец показывает уже вниз. Изобразим вектор $⃗ d$ на рисунке:

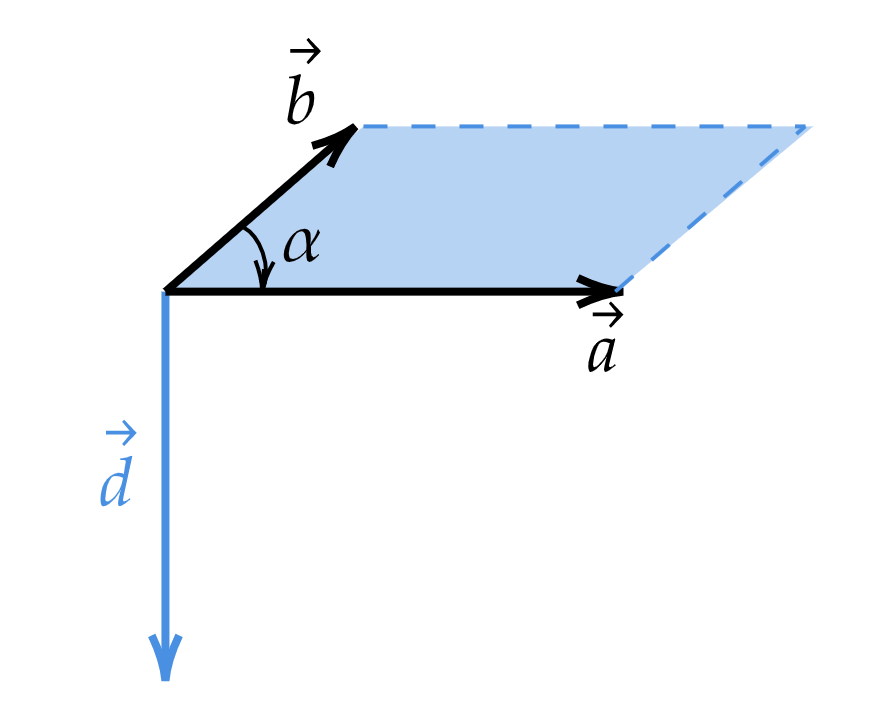
Таким образом, векторное произведение векторов не обладает коммутативностью. Например, если $2 ⋅3 = 3⋅2 = 6$ , то в случае с векторным произведением векторов $⃗a × ⃗b ⁄= ⃗b× ⃗a$ . Векторное произведение векторов является антикоммутативным, то есть

⃗ ⃗ ⃗a × b = − b× ⃗a

Силы в магнитном поле: векторное представление

1. Сила Ампера: $|------------| |⃗FА = I ⋅[⃗l,B ⃗] -------------$

Вектор $⃗l$ равен по модулю длине проводника, а по направлению совпадает с направлением тока в проводнике.

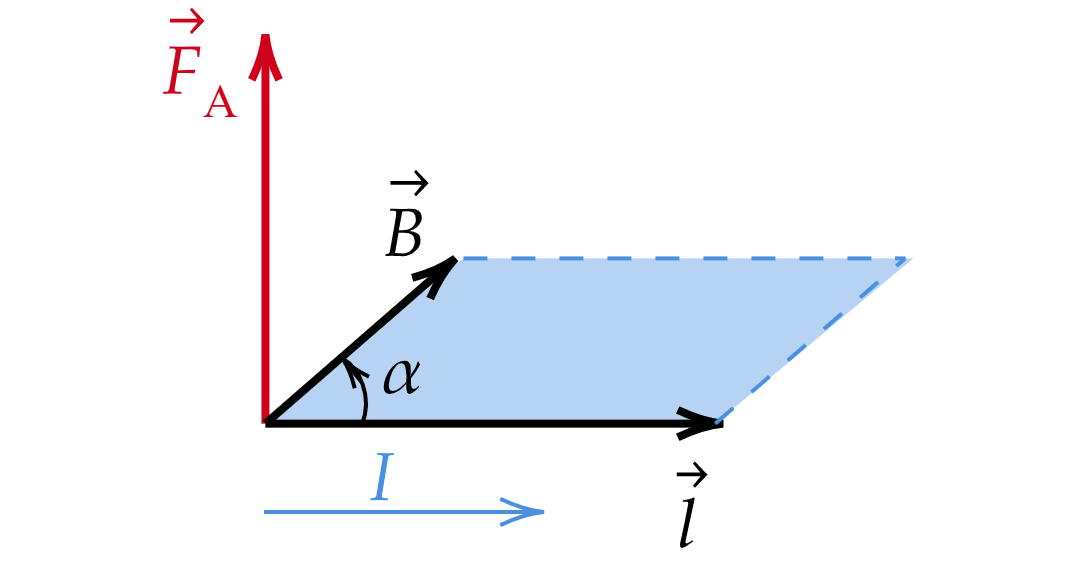
2. Сила Лоренца: $|------------| |⃗FЛ = q⋅[⃗v, ⃗B] --------------$

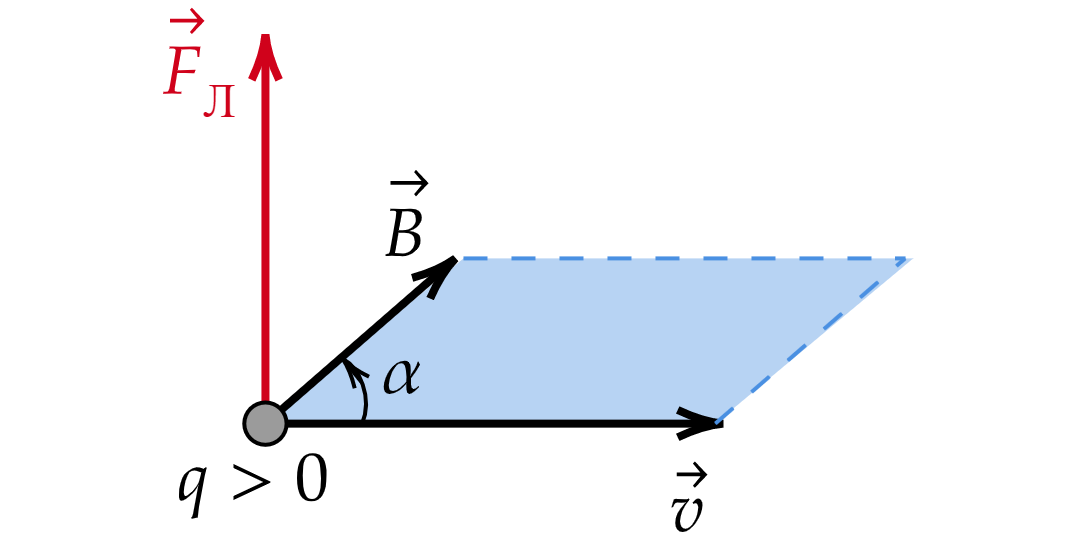
Таким образом, направление силы Лоренца и силы Ампера можно определить не только по правилу левой руки, но и исходя из векторного представления данных сил. Если Вы выбираете для себя данный способ, то обязательно запомните, в каком порядке умножаются векторы $⃗l$ и $B⃗$ , $⃗v$ и $⃗B$ . Это является ключевым моментом при определении направления сил Ампера и Лоренца данным способом.

Предыдущая справка

Следующая справка