Задачи на прямолинейное движение —Каталог задач по ЕГЭ - Математика

Ошибка.
Попробуйте повторить позже

Задача 1#1609

Из двух городов, расстояние между которыми равно 840 км, одновременно навстречу друг другу выехали два автомобилиста. Скорость первого 70 км/ч, а скорость второго 60 км/ч. Через сколько часов они встретились, если известно, что автомобиль первого автомобилиста сломался на полпути между этими городами и на его починку пришлось потратить час.

Показать ответ и решение

Половина расстояния между городами 420 км. Это расстояние первый автомобилист преодолел за 6 часов, а второй автомобилист за 7 часов.

Так как первый сломался на полпути между городами, то через 7 часов после начала движения он также был на полпути между городами, то есть, через 7 часов они встретились.

Ответ: 7

Ошибка.
Попробуйте повторить позже

Задача 2#23560

Расстояние между городами A и B равно 435 км. Из города A в город B со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах.

Показать ответ и решение

На момент выезда второго автомобиля первый проедет 60 км, то есть будет на расстоянии 60 км от города А. Начиная с этого момента, автомобили будут сближаться со скоростью $60+ 65 = 125$ км/ч и встретятся через $317525-= 3$ часа.

Получаем, что суммарно первый автомобиль провел в движении $1+ 3= 4$ часа со своей постоянной скоростью 60 км/ч, за это время он удалился от города А на $60⋅4= 240$ км.

Ответ: 240

Ошибка.
Попробуйте повторить позже

Задача 3#288

Из пункта А в пункт В выехал мотоциклист. Через полчаса после прибытия в B он выехал обратно и одновременно с этим навстречу ему выехал второй мотоциклист из А. Из-за поломки скорость первого мотоциклиста на обратном пути уменьшилась в 3 раза по сравнению с первоначальной. Скорость второго мотоциклиста оказалась на 20 км/ч больше, чем первоначальная скорость первого. Время, через которое произошла встреча, оказалось в два раза меньше, чем время, которое первый потратил на дорогу из А в В. Найдите скорость второго мотоциклиста в км/ч.

Показать ответ и решение

Пусть t ч – время, которое затратил первый мотоциклист на путь из А в В,

$v$ км/ч – первоначальная скорость первого мотоциклиста.

Тогда расстояние между пунктами А и В равно $v ⋅ t$ км, расстояние, которое проехал первый мотоциклист из В до места встречи, равно

1 -v ⋅ 0,5t км, 3

а расстояние, которое проехал второй мотоциклист из А до места встречи, равно

(v + 20) ⋅ 0,5t к м.

Так как сумма расстояний, которые они одновременно проехали до места встречи, равна расстоянию от А до В, то

1 1 vt = -v ⋅ 0,5t + (v + 20) ⋅ 0, 5t ⇔ --vt = 10t, 3 3

откуда находим $v = 30$ и, следовательно, скорость второго мотоциклиста равна $v + 20 = 50$ км/ч.

Ответ: 50

Ошибка.
Попробуйте повторить позже

Задача 4#289

Из пункта А в пункт В вышел турист. Одновременно с этим из пункта В в пункт А выбежал бегун. Турист шёл весь путь с постоянной скоростью. Бегун бежал первую треть пути из А в В со скоростью 10 км/ч, а всё оставшееся расстояние со скоростью в два раза большей, чем скорость туриста. Найдите скорость туриста, если до места встречи с бегуном он успел пройти треть пути из А в В. Ответ дайте в км/ч.

Показать ответ и решение

Пусть S км – расстояние между А и В,

$v$ км/ч – скорость туриста.

Тогда время, которое турист шёл до места встречи, равно

1S -3-, v

время, которое бегун потратил на первую треть пути, равно

1 -3S 10,

а время, которое бегун потратил на вторую треть пути (то есть на путь до места встречи), равно

1 -3S. 2v

Так как турист и бегун начали движение одновременно, то

13S 13S 13S 10S vS 5S -v- = -10 + -2v ⇔ 30v- = 30v-+ 30v-,

откуда получаем $v = 5$ км/ч.

Ответ: 5

Ошибка.
Попробуйте повторить позже

Задача 5#690

Лыжник планировал проехать 4 км с горы с постоянной скоростью $v$ км/ч. Вместо этого первые 2 километра он проехал в два раза быстрее, чем планировал, а оставшиеся 2 километра он проехал в два раза медленнее, чем планировал. Во сколько раз больше времени ушло у лыжника на самом деле, чем должно было бы уйти, если бы всё в его жизни было по плану?

Показать ответ и решение

Пусть по плану на весь маршрут лыжника должно было уйти $t$ часов. Тогда на первые 2 километра (которые составляют половину пути) у лыжника ушло время в часах, равное

1 1 t⋅2 ⋅2 =0,25t

На оставшиеся 2 километра ушло время в часах, равное

t⋅ 1 ⋅2 = t 2

Следовательно, на весь путь ушло $1,25t$ часа, то есть в $1,25$ раза больше, чем было запланировано изначально.

Ответ: 1,25

Ошибка.
Попробуйте повторить позже

Задача 6#927

Бегун Вася установил рекорд на дистанции $L$ метров, пробежав её с постоянной скоростью $v$ км/ч (его время наименьшее за всю историю человечества). Илья хочет повторить результат Васи или побить его рекорд. Он знает, что в течение некоторого времени он сможет поддерживать скорость $1,2v$ км/ч, а потом его скорость упадёт до $0,8v$ км/ч и сохранится такой до конца дистанции. Какую часть дистанции Илья должен поддерживать скорость $1,2v$ км/ч, чтобы результат его устроил? Если в задаче возможны несколько ответов – выберите наименьший.

Показать ответ и решение

Обозначим через $l$ км длину первого участка (где скорость Ильи равна $1,2v$ км/ч), тогда суммарное время Ильи на всей дистанции равно

--l-- L-−--l 1,2v + 0,8v

Так как Илью устроит любое время, не большее, чем у Васи, то

l L − l L -----+ ------≤ --, 1,2v 0,8v v

что равносильно

l 0,8l + 1,2(L − l) ≤ 0,96L ⇔ l ≥ 0,6L ⇔ -- ≥ 0,6. L

Таким образом, наименьший ответ равен $0,6$ .

Ответ: 0,6

Ошибка.
Попробуйте повторить позже

Задача 7#1005

Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 117 км. На следующий день он отправился обратно в А со скоростью на 4 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.

Показать ответ и решение

Изобразим в виде схемы движение велосипедиста:

$PIC$

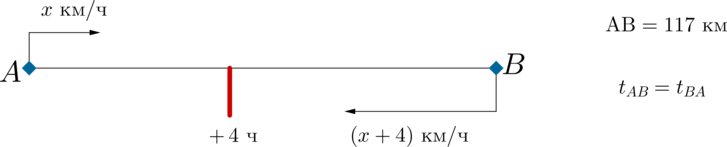
Время в часах, которое он затратил на дорогу из A в B, равно

117 tAB = x

Время в часах, которое он затратил на дорогу из В в А, учитывая остановку, равно

117 tBA = 4+ x-+4-

Так как $tAB = tBA,$ то получаем уравнение:

117 -117- x = 4+ x + 4

Домножим обе части уравнения на $x(x+ 4),$ так как $x ⁄= 0, x+ 4⁄= 0:$

117(x+ 4)= 4x(x + 4) +117x 117x + 117 ⋅4 = 4(x2+ 4x)+ 117x 4(x2+ 4x) − 117⋅4 =0 2 x + 4x− 117= 0

Найдем дискриминант:

2 2 D = 4 + 117 ⋅4= 4(4 +117)= 4⋅121= (2⋅11)

Следовательно, корни уравнения $x1 =− 13$ и $x2 = 9.$ Так как скорость не может быть отрицательной, то $x= 9.$ Тогда скорость велосипедиста на пути из В в А равна $x+ 4= 13.$

Ответ: 13

Ошибка.
Попробуйте повторить позже

Задача 8#1026

Из пункта А в пункт Б одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй первую половину пути проехал со скоростью $84$ км/ч, а вторую половину пути со скоростью, на $11,2$ км/ч меньшей скорости первого, в результате чего оба автомобилиста прибыли в пункт Б одновременно. Найдите скорость первого автомобилиста, если известно, что она была больше 50 км/ч. Ответ дайте в км/ч.

Показать ответ и решение

Пусть скорость первого автомобилиста равна $x$ км/ч, $S$ км – расстояние от А до Б. Тогда можно составить такую картинку-схему:

$PIC$

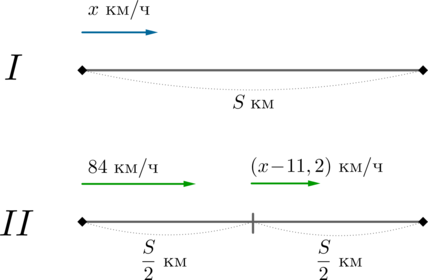
Тогда время в часах, которое первый затратил на дорогу, равно

S- x

Время в часах, которое второй затратил на дорогу, равно

S- S- -2-+ ---2----- 84 x − 11,2

Так как оба прибыли одновременно в пункт Б, то есть затратили на дорогу одинаковое время, то получаем следующее уравнение:

S S2- S2- --= ---+ --------- x 84 x − 11,2

Заметим, что можно разделить обе части уравнения на $S$ , так как $S ⁄= 0$ . Приведем к общему знаменателю и перенесем все слагаемые в одну сторону:

2 x--−-(84-+-11,2-)x-+-2-⋅ 84-⋅ 11,2-= 0 2 ⋅ 84 ⋅ x ⋅ (x − 11,2)

Решим уравнение $2 x − (84 + 11,2 )x + 2 ⋅ 84 ⋅ 11,2 = 0$ . Домножим его на $10$ : $2 10x − 952x + 2 ⋅ 84 ⋅ 112 = 0$ .
Дискриминант

D = 9522 − 4 ⋅ 10 ⋅ 2 ⋅ 84 ⋅ 112 = 72 ⋅ 26 ⋅ 172 − 210 ⋅ 3 ⋅ 5 ⋅ 72 = 72 ⋅ 26 ⋅ (289 − 240) = (7 ⋅ 23 ⋅ 7 )2 = 3922

Следовательно, корнями будут

x1 = 952-+-392-= 67,2 и x2 = 952-−-392- = 28 20 20

Так как скорость больше 50, то ответом будет число 67,2.

Ответ: 67,2

Ошибка.
Попробуйте повторить позже

Задача 9#1029

Из пункта А в пункт С выехал мотоциклист, скорость которого 16 км/ч. Одновременно с ним из пункта В, находящегося между пунктами А и С, в пункт С выехал второй мотоциклист, скорость которого 31 км/ч. Расстояние между пунктами A и B равно 10 км. Через сколько минут расстояние между мотоциклистами будет равно 17,5 км? Если задача допускает несколько вариантов ответа, в бланке укажите их сумму.

Показать ответ и решение

$PIC$

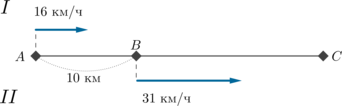
Заметим, что так как более быстрый мотоциклист находится впереди, то расстояние между мотоциклистами будет только увеличиваться (то есть они будут только отдаляться друг от друга). Значит, в задаче будет только один ответ.

Следовательно, расстояние между ними должно измениться на $17,5− 10= 7,5$ км (так как изначально они находились на расстоянии 10 км друг от друга). Скорость удаления мотоциклистов равна $31− 16= 15$ км/ч. Следовательно, время, через которое расстояние между ними увеличится еще на 7,5 км, равно $7,5:15= 0,5$ часа, или 30 минут.

Ответ: 30

Ошибка.
Попробуйте повторить позже

Задача 10#1613

Два туриста одновременно вышли в одном направлении в город N. При этом вышли они из разных городов, расстояние между которыми 9 км. Известно, что турист, изначально находившийся дальше от города N, шёл со скоростью, в два раза превышающей скорость другого туриста. В город N они прибыли одновременно, через 3 часа после начала движения. Найдите скорость туриста, который шёл быстрее. Ответ дайте в км/ч.

Показать ответ и решение

Пусть $v$ км/ч – скорость медленного туриста.

Тогда расстояние, которое прошёл медленный турист, равно $3v$ , а расстояние, которое прошёл быстрый турист, равно $2v ⋅ 3 = 6v$ .

Так как быстрый турист прошёл на 9 км больше, то:

6v − 3v = 9,

откуда находим $v = 3$ км/ч, значит скорость быстрого туриста $2 ⋅ 3 = 6$ км/ч.

Ответ: 6

Ошибка.
Попробуйте повторить позже

Задача 11#1614

Два велосипедиста одновременно выехали из пункта C в пункт D с одинаковой скоростью. Расстояние между пунктом D и пунктом C – 30 км. Проехав первую треть пути с постоянной скоростью, первый велосипедист увеличил скорость в два раза и ехал с ней до D, а второй велосипедист всю дорогу ехал с постоянной скоростью. Найдите первоначальную скорость обоих велосипедистов, если в D второй велосипедист прибыл на час позже первого. Ответ дайте в км/ч.

Показать ответ и решение

Пусть $v$ км/ч – стартовая скорость велосипедистов.

Тогда время, которое потратил на путь второй велосипедист, равно

30- v ,

время, которое потратил на первую треть пути первый велосипедист, равно

1 ⋅ 30 3----, v

а время, которое потратил на оставшуюся часть пути первый велосипедист, равно

2 3-⋅ 30. 2v

Так как первый прибыл в пункт D на час раньше, то:

13 ⋅ 30 23 ⋅ 30 30 10 10 30 v --v---+ --2v--= -v-− 1 ⇔ -v-+ v--= -v-− v- ⇔ 20 = 30 − v

– при $v ⁄= 0$ , откуда находим $v = 10$ км/ч.

Ответ: 10

Ошибка.
Попробуйте повторить позже

Задача 12#1984

Лыжник планировал проехать $10$ с горы за $20$ минут с постоянной скоростью $v$ . Вместо этого первые несколько километров он проехал в два раза быстрее, чем планировал, а оставшиеся километры он проехал в два раза медленнее, чем планировал. В итоге весь путь занял у него $34$ минуты. Сколько километров лыжник проехал в два раза быстрее, чем планировал?

Показать ответ и решение

Пусть $t$ – время, которое лыжник должен был потратить на те самые несколько километров, которые он ехал быстрее, чем планировал. Тогда время, на самом деле затраченное лыжником, есть

1 t ⋅2-+ (20 − t) ⋅ 2 = 34 ⇔ t = 4,

следовательно, на те самые несколько километров, которые он ехал быстрее, лыжник должен был потратить $4--= 1- 20 5$ часть всего времени. Так как скорость лыжника должна была быть постоянной, то расстояние, которое он ехал быстрее, равно

1 10 ⋅--= 2. 5

Ответ: 2

Ошибка.
Попробуйте повторить позже

Задача 13#2190

Два автомобиля выехали с постоянными скоростями из пунктов $A$ и $B$ навстречу друг другу. Известно, что скорость одного из них в $1, 2$ раза больше, чем скорость другого. Они встретелись через $t$ часов. Известно, что медленному автомобилю понадобилось $T$ часов, чтобы добраться до противоположного пункта. Найдите $T -- t$ .

Показать ответ и решение

Пусть $v∕$ – скорость медленного автомобиля, тогда $1, 2v∕$ – скорость быстрого автомобиля, следовательно, скорость сближения автомобилей равна $v + 1,2v = 2, 2v∕$ .

Пусть $S$ – расстояние между пунктами $A$ и $B$ , тогда $S t = ----- 2,2v$ , а $S T = -- v$ , следовательно,

T-= S-: -S---= 2, 2. t v 2,2v

Ответ: 2,2

Ошибка.
Попробуйте повторить позже

Задача 14#2341

Альпинистка Маша начала ползти по стене, находясь на высоте $2,75$ м от пола. За каждую минуту она поднималась бы на $1,5$ м, но ветер тут же сносит ее вниз на $0, 25$ м. Сколько минут она ползет, если теперь она находится на высоте $14$ м от пола?

Показать ответ и решение

Так как Маша уже находилась на высоте 2,75 м, то проползла она за время наблюдения $14 − 2,75 = 11,25$ метров. Заметим, что в итоге за каждую минуту она поднимается на 1,25 метров. Следовательно, время, которое она затратила на подъем, равно

11,25 : 1,25 = 9 м инут.

Ответ: 9

Ошибка.
Попробуйте повторить позже

Задача 15#2345

Если два велосипедиста стартуют из одной точки в одном направлении, то через 6 часов расстояние между ними будет равно 48 км. На сколько километров назад от точки старта должен отъехать более быстрый велосипедист до начала движения, чтобы догнать менее быстрого через 3,5 часа, если скорость менее быстрого равна 10 км/ч?

Показать ответ и решение

$PIC$

Пусть $x$ км/ч — скорость быстрого велосипедиста, следовательно, $x> 10.$ Тогда $x− 10$ км/ч — скорость, с которой быстрый удаляется от медленного. Значит, за 6 часов он удалится от медленного на $6⋅(x− 10)$ км. Тогда получаем уравнение:

6(x − 10)= 48 ⇒ x =18

$PIC$

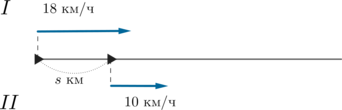
За 3,5 часа медленный проедет 35 км, следовательно, если быстрому нужно отъехать назад на $s$ км, то он должен за 3,5 часа проехать $s+ 35$ км. Тогда имеем уравнение:

18⋅3,5= s +35

Отсюда $s= 28$ км.

Ответ: 28

Ошибка.
Попробуйте повторить позже

Задача 16#2346

Из города N в город M, расстояние между которыми 36 км, выехал автомобиль со скоростью 46 км/ч. Одновременно с ним из города M в том же направлении выехал другой автомобиль со скоростью 40 км/ч. Через сколько часов расстояние между автомобилями будет равно 21 км? Если задача допускает несколько вариантов ответа, в бланке укажите их сумму.

Показать ответ и решение

Заметим, что так как впереди находится второй (медленный) автомобиль, то сначала автомобили будут сближаться (до того момента, как первый догонит второго), а затем будут удаляться.

Так как расстояние между ними в начале движения 36 км и $36> 21,$ то первый раз расстояние в 21 км между ними будет, пока они сближаются, а второй раз — когда они будут отдаляться.

$PIC$

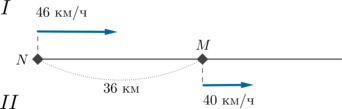
Скорость сближения автомобилей равна $46− 40= 6$ км/ч. Расстояние между ними должно измениться с 36 км до 21 км, то есть на $36− 21= 15$ км. Следовательно, первый раз это произойдет через $15:6= 2,5$ часа.

Теперь найдем, через сколько часов после начала движения первый догонит второго. Это значит, что расстояние между ними должно стать равным 0 км. Значит, должно измениться на 36 км. Следовательно, время встречи равно $36 :6 = 6$ часов.

Значит, спустя 6 часов движения картинка выглядит так:

$PIC$

Скорость отдаления также равна 6 км/ч. Расстояние между ними должно измениться с 0 км до 21 км, следовательно, на 21 км, следовательно, это произойдет через $21:6= 3,5$ часа после встречи. Значит, второй раз расстояние между ними будет равно 21 км через $6+ 3,5 = 9,5$ часов. Так как в задаче два ответа, то в бланк мы запишем $2,5+ 9,5= 12.$

Ответ: 12

Ошибка.
Попробуйте повторить позже

Задача 17#2698

Два брата пробежали марафон длиной 42 километра. Оба брата бежали марафон с постоянной скоростью, причём скорость младшего была на 1 км/ч больше, чем скорость старшего, в результате чего он прибыл к финишу на 1 час раньше. С какой скоростью бежал старший из братьев? Ответ дайте в км/ч.

Показать ответ и решение

Пусть $v$ км/ч — скорость старшего брата.

Тогда время, за которое старший брат пробежал марафон, равно $42 v$ ч, а время младшего брата равно $-42- v+ 1$ ч.

Так как младший брат пробежал марафон на 1 час быстрее, чем старший, то

42= -42- + 1 ⇔ 42(v +1)= 42v+ v(v+ 1) v v +1

— при $v ⁄= 0,$ $v ⁄= −1,$ что равносильно

2 v + v− 42= 0

Отсюда находим $v1 = 6,$ $v2 = − 7.$ Таким образом, скорость старшего брата равна 6 км/ч.

Ответ: 6

Ошибка.
Попробуйте повторить позже

Задача 18#12977

Дорога между пунктами $A$ и $B$ состоит из подъёма и спуска, а её длина равна 36 км. Путь из $A$ в $B$ занял у туриста 10 часов, из которых 2 часа ушло на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 3 км/ч. Ответ дайте в км/ч.

Показать ответ и решение

Поскольку на спуск ушло 2 часа, то на подъём ушло $10− 2= 8$ часов. Пусть $x$ км/ч — скорость на подъёме. Составим таблицу:


	$S,$ км	$v,$ км/ч	$t,$ ч

Подъём	$8x$	$x$	8

Спуск	$2(x+ 3)$	$x+ 3$	2

Поскольку длина всего пути 36 км, то получим уравнение:

$pict$

Тогда скорость туриста на спуске равна $3 +3 = 6$ км/ч.

Ответ: 6

Ошибка.
Попробуйте повторить позже

Задача 19#14913

За 200 км до станции назначения поезд был задержан у семафора на час. Затем машинист увеличил на 10 км/ч скорость, с которой поезд ехал до остановки и прибыл в пункт назначения по расписанию. С какой скоростью поезд ехал после остановки? Ответ дайте в км/ч.

Показать ответ и решение

Пусть $v$ — начальная скорость поезда. Время, которое планировалось затратить на преодоление 200 км, составляет $200 v$ часа. Из-за задержки и увеличения скорости поезд в итоге затратил $-200- +1 v +10$ часов. Поезд прибыл по расписанию, тогда приравняем полученные выражения:

$pict$

Корень $x1$ не подходит по условию, значит, начальная скорость поезда равна 40 км/ч. Тогда после остановки поезд ехал со скоростью $40 +10 = 50$ км/ч.

Ответ: 50

Ошибка.
Попробуйте повторить позже

Задача 20#16749

Велосипедист выехал с постоянной скоростью из города $A$ в город $B,$ расстояние между которыми равно 104 км. На следующий день он отправился обратно со скоростью, на 5 км/ч больше прежней. По дороге велосипедист сделал остановку на 5 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из $A$ в $B.$ Найдите скорость велосипедиста на пути из $A$ в $B.$ Ответ дайте в км/ч.