Тема №6 Механика (изменение физических величин в процессах и установление соответствия)

07 Кинематика. Установление соответствия

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела №6 механика (изменение физических величин в процессах и установление соответствия)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#14002

Тело движется вдоль оси $Ox$ из начала координат с постоянным ускорением. Направления начальной скорости и ускорения $a$ тела указаны на рисунке.

Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные под соответствующими буквами.

Ф изические величины Формулы at2- А) К оордината x тела в м омент времени t; 1) v0t+ 22 Б ) Скорость vx тела в момент времени t. 2) v0t− at 2 3) v0− at 4) v0+ at

|----|---| |-A--|Б--| ---------|

Показать ответ и решение

Проекция вектора ускорения $⃗a$ на ось $Ox$ : $ax =− a$ . Проекция вектора начальной скорости $⃗υ0$ на ось $Ox$ : $vx = v0$ . Так как тело начинает движение из начала координат, координата тела $x$ в момент времени $t$ :

at2 x= υ0t− 2--

(А — 2)

Скорость $υx$ тела в момент времени t:

v = v − at x 0

(Б — 3)

Ответ: 23

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#14003

Тело первую половину пути проходит со скоростью $υ1$ , а вторую – со скоростью $υ2$ . Как изменится средняя скорость на всём пути, если

А ) увеличить весь путь в 2 раза, 1) увеличится в 2 раза Б ) увеличить каждую из скоростей в 2 раза, 2) увеличится в 4 раза 3) уменьшится в 2 раза 4) уменьшится в 4 раза 5) не изм енится

Запишите в таблицу выбранные цифры под соответствующими буквами.

|----|---| |-A--|Б--| ---------|

Показать ответ и решение

Средняя скорость на всём пути:

S1 +S2 υср =-t1-+t2 .

Пусть весь путь $S = 2l$ , тогда $S1 = l$ , $S2 = l$ , $t1 = l- υ1$ , $t2 =-l υ2$ .

Отсюда

υ ср = --2l---= -2υ1υ2-. -l+ -l υ1+ υ2 υ1 υ2

Значит средняя скорость зависит только от скоростей $υ1$ и $υ2$ на каждой из половин пути и не зависит от длины самого пути, поэтому вопросу А соответствует 5.

В других случаях, поскольку $υ1$ и $υ2$ изменяются в одинаковое число раз, средняя скорость изменяется пропорционально изменению одной из скоростей $⇒$ Б = 1

Ответ: 51

Ошибка.
Попробуйте повторить позже

Задача 3#14005

Четыре байкера движутся по прямому шоссе с одинаковыми скоростями $υ$ , 1 и 2 – на концерт (в одном направлении (вдоль оси $Ox$ )), а 3 и 4 – им навстречу с концерта. Определите проекции их относительных скоростей на ось $Ox$ .

А ) 2 относительно 1 1) υ Б) 1 относительно 3 2) 2υ 3)−υ 4)− 2υ 5) 0

Запишите в таблицу выбранные цифры под соответствующими буквами.

--------- | A |Б | |----|---| ---------|

Показать ответ и решение

Проекция на ось $Ox$ скорости любого байкера из первой пары относительно любого из второй пары:

′ υотн1 =υ − (− υ)= 2υ

И наоборот, проекция относительной скорости любого байкера из второй пары в системе отсчёта первой:

′ υотн2 =− υ− υ = − 2υ

Внутри каждой из пары байкеры покоятся друг относительно друга, т.е. для них относительная скорость равна нулю.

Ответ: 52

Ошибка.
Попробуйте повторить позже

Задача 4#14006

Бэтмобиль, двигаясь ускоренно, имел в начальной точке трассы скорость $υ0$ , через некоторое время в конечной точке трассы скорость $υ2$ . Укажите выражения для:

(υ + υ ) А) скорости бэтм обиля на половине этого расстояния 1)∘-02--2-- (υ20 +-υ22) Б) средней скорости бэтмобиля на всём пути 2) 2 3)(υ2−-υ0)- ∘ --22---2- 4) (υ2 −-υ0) 2

Запишите в таблицу выбранные цифры под соответствующими буквами.

|----|---| | A |Б | |----|---| ---------|

Показать ответ и решение

При равноускоренном движении с начальной скоростью $υ0$ весь путь будет равен:

υ22 − υ20 S = --2a--

для первой половины пути:

2 2 S-= υ1 −-υ0 2 2a

где $v1$ — скорость на половине пути

2 2 2 2 2(v1 − v0)= v2 − v0

∘ (υ20 +-υ22) υ1 = ---2----

Скорость при равноускоренном движении меняется линейно:

v = v0+ at

Средняя величина при линейной зависимости определяется как среднее арифметическое начального и конечного значения. Средняя скорость на всём пути равна:

(υ0+-υ2)- υ ср = 2

Ответ: 21

Ошибка.
Попробуйте повторить позже

Задача 5#14007

Установите соответствие между зависимостью проекции скорости тела от времени и зависимостью проекции перемещения этого тела от времени для одного и того же движения (все величины выражены в СИ).

|-----------------|--------------------| |П-роекция-скорости-|П-роекция-перем-ещ-ения| | | | | А)υx = 3− 2t | 1)Sx = 5t +2t2 | | Б)υx = 5+ 4t | 2)Sx = 5t +4t2 | | | 3)S = 3t − 2t2 | | | x 2 | -----------------------4)Sx =-3t−-t-----

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

|--|--| |А-|Б-| -------

Источники: Демидова 2019

Показать ответ и решение

I способ
Скорость – это производная от координаты (перемещения) по времени. Из кинематических уравнений

a t2 x= x0+ v0xt+ -x2- vx = (x′)= v0x+ axt

Возьмем производную от четырех формул, а дальше сделаем соответствие: Возьмем производную от четырех формул, а дальше сделаем соответствие:
1) $2 Sx = 5t+2t$ , производная от величины в первой степени $′ (at) =a$ , то есть $′ (5t) = 5$ , производная от величины во второй степени $2 ′ (bt ) =2bt$ , в нашем случае $2 2t = 4t$ .

υx =S ′(x)= 5+ 4t

Ответ – Б
2) $Sx = 5t+4t2$ , производная от величины в первой степени $(at)′ =a$ , то есть $(5t)′ = 5$ , производная от величины во второй степени $(bt2)′ =2bt$ , в нашем случае $4t2 = 8t$ .

′ υx =S (x)= 5+ 8t

3) $S =3t− 2t2 x$ , производная от величины в первой степени $(at)′ = a$ , то есть $(3t)′ = 3$ , производная от величины во второй степени $2 ′ (bt ) =2bt$ , в нашем случае $2 − 2t = −4t$ .

υx =S ′(x)= 3− 4t

4) $2 Sx =3t− t$ , производная от величины в первой степени $′ (at)= a$ , то есть $′ (3t)= 3$ , производная от величины во второй степени $(bt2)′ =2bt$ , в нашем случае $− t2 = −2t$ .

υx =S ′(x)= 3− 2t

Ответ – А
II способ
А) Посмотрим на зависимость $vx = v0x+ axt$ и на зависимость из условия $x =3 − 2t$ , сопоставляя величины, получаем, что $v0x = 3$ , $ax = − 2$ , а с учетом уравнения кинематики $axt2 x= x0+ v0xt+ 2$ получаем $2 x= x0+ 3t− t$ (4). Б) Аналогично пункту А) $v = 5+ 4t$ : $v0x = 5$ , $ax =4$ . Следовательно, $x= x0+ 5t+ 2t2$ (1).

Ответ: 41

Ошибка.
Попробуйте повторить позже

Задача 6#14008

Установите соответствие между зависимостью координаты материальной точки (все значения выражены в СИ) и значениями его начальной координаты и проекцией ускорения на ось $Ox$ .

К каждой позиции первого столбца подберите подходящую позицию из второго столбца. В ответ укажите последовательность чисел.

|-------------------------|---------------------------------------| |УРАВ НЕН ИЕ ДВИ Ж ЕНИ Я: |НАЧА ЛЬН АЯ КО ОРД ИНАТ А, УС КОРЕ НИЕ:| |----А)-x=-2+-5t−-3t2------|----------1) x-=-0,a-=-7-м/с2-----------| | | 0 x 2 | | Б) x = 7t | 2) x0 = 2 м,ax = −6 м/с | | | 3) x0 = 2 м,ax = −3 м/с2 | -------------------------------------4) x0-=-0,ax =-0-м/с2----------

|--|--| |A-|Б-| | | | -------

Показать ответ и решение

Основное уравнение кинематики показывает зависимость координаты $x$ от времени $t$ :

axt2 x= x0+ υ0xt+ -2--

где $x0$ – начальная координата, $υ0x$ – проекция начальной скорости на ось $Ox$ , $ax$ – проекция ускорения на ось $Ox$ .

A – 2

Рассмотрим данное уравнение:

2 x= 2+ 5t− 3t

Сопоставив его с основным уравнением кинематики, можно увидеть, что $x0 = 2 м,ax = −6 м/ с2$ .

Б – 4

Рассмотрим данное уравнение:

x = 7t

Сопоставив его с основным уравнением кинематики, можно увидеть, что $2 x0 = 0 м,ax =0 м/с$ (тело движется прямолинейно, без ускорения).

Для условий 1 и 3 уравнения будут выглядеть соответственно:

x = 3,5t2

= 2 +υ0t− 1,5t2

Ответ: 24

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#14009

Небольшое тело кидают с начальной скорость $υ0$ под углом $α$ к горизонту. Найдите дальность полёта $L$ и максимальную высоту подъёма $H$ . Силой сопротивления воздуха пренебречь.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца.В ответ укажите последовательность цифр.

|------------------------|------------| |------ВЕЛ-ИЧ-ИНА:-------|Ф-ОРМ-УЛ-А:-| | | v20sin-2α | | А) Дальность полёта, L | 1) 2g | |Б) Максимальная высота, H|2) υ20-⋅2-cosα| | | 2 g | | |3) υ0 ⋅sin2α | | | υ2⋅gsin2α | | |4) -0-2g---- | --------------------------------------

|--|--| |A |Б | |--|--| -------

Показать ответ и решение

1) Найдём проекции начальной скорости $υ$ на оси $Ox$ и $Oy$ :

По рисунку видно, что

υx = υ0cosα

υy = υ0sin α

2) Так как на тело действует только сила тяжести, то у него есть только вертикальная составляющая ускорения $a = g$ , которое направлено против оси Оу. Значит, зависимости координаты по осям Оу и Ох от времени t в нашем случае будут выглядеть так:

y =υ0 ⋅tsin α− gt2 2

x = υ0⋅tcosα

3)Через время $t0$ — полное время полёта координата по оси $Oy$ будет равна нулю (тело упадёт на землю), значит:

2 0= υ0⋅t0sinα− gt0 2

υ0⋅t0sinα = gt20-⇒ 2

2υ0⋅sinα t0 =---g----

4)Подставив это значение в уравнение зависимости координаты $x$ , получим расстояние, которое пролетит тело за время $t0$ , а это и есть искомая дальность полёта:

x = L= υ0⋅cosα ⋅ 2υ0-⋅sinα g

L = υ20 ⋅sin-2α-⇒ А – 3 g

5) Так как силой сопротивления воздуха пренебрегаем, то траектория движения тела — парабола, значит, тело достигает наивысшей траектории в момент времени $t0 2$ :

( )2 y = H = υ⋅sin α⋅ υ0⋅sin-α− g ⋅ υ0⋅sin-α g 2 g

υ20 ⋅sin2α υ20 ⋅sin2α υ20 ⋅sin2α H = ---g----− ---2g---= ---2g---⇒ Б – 4

Ответ: 34

Ошибка.
Попробуйте повторить позже

Задача 8#14028

В момент $t =0$ мячик бросают с начальной скоростью $v0$ под углом $α$ к горизонту с балкона высотой $h$ (см. рисунок). Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t.

Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня $y = 0$ ) К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) проекция импульса мячика на ось y
2) кинетическая энергия мячика
3) модуль ускорения мячика a
4) потенциальная энергия мячика

|--|--| |А-|Б-| -------

Источники: Демоверсия 2018

Показать ответ и решение

А) Единственная постоянная величина из данного списка это ускорение, в данном случае свободного падения.
Б) График представляет собой параболу, следовательно, это либо кинетическая либо потенциальная энергия, но так как ветки параболы направлены вверх, то это кинетическая энергия.

Ответ: 32

Ошибка.
Попробуйте повторить позже

Задача 9#15638

Выражения А и Б определяют зависимость координат двух тел от времени.
Установите соответствие между зависимостью координаты тела от времени и зависимостью проекции скорости от времени для этого же тела (все величины заданы в СИ). К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

|-----------------|-------------| |--КОО-РДИН-АТА---|-СКО-РОСТ-Ь--| |А) x= 25− 4t+ 3t2 |1) vx = 25− 4t | Б ) x= 30− 6t |2) v = 6t− 4 | | | x | | | 3) vx = −6 | ---------------------4) vx =-6t-|

Показать ответ и решение

I способ
Скорость – это производная от координаты (перемещения) по времени. Из кинематических уравнений

a t2 x= x0+ v0xt+ -x2- vx = (x′)= v0x+ axt

А) $x = 25− 4t+3t2$ Производная от константы равна нулю $(25)′ = 0$ , производная от величины в первой степени $(at)′ =a$ , то есть $(−4t)′ = − 4$ , производная от величины во второй степени $(bt2)′ = 2bt$ , в нашем случае $3t2 = 6t$ . Объединяем $vx = − 4+ 6t$

Б) $x = 30− 6t$ Производная от константы равна нулю $′ (30)= 0$ , производная от величины в первой степени $′ (at) = a$ , то есть $(−6t)′ =− 6$ . Объединяем $vx = −6$ .
II способ
А) Посмотрим на зависимость $x = x0+ v0xt+ axt2 2$ и на зависимость из условия $x= 25− 4t+ 3t2$ , сопоставляя величины, получаем, что $x =25 0$ , $v = − 4 0x$ , $a = 6 x$ , а с учетом уравнения кинематики $v = v + a t x 0x x$ получаем $v = − 4+ 6t x$ . Б) Аналогично пункту А) $x = 30− 6t$ : $x0 = 30$ , $v0x = − 6$ , $ax = 0$ . Следовательно, $vx = − 6+ 0⋅t= −6$ .

Ответ: 23

Ошибка.
Попробуйте повторить позже

Задача 10#20548

В момент $t =0$ шарик бросили вертикально вверх с начальной скоростью v (см. рисунок). Сопротивление воздуха пренебрежимо малo. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять ( $t0$ - время полёта).

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Показать ответ и решение

Рассмотрим, как зависят от времени указанные величины.
1) Координата $y$ описывается уравнением:

gt2 y(t)= vt− -2-,

где $g$ – ускорение свободного падения.
То есть парабола с ветвями, направленными вниз (График Б) 2) Скорость шарика по вертикали равна:

v (t)= v − gt, y

То есть прямая, направленная вниз (График – А)
3) Проекция ускорения шарика всюду постоянна и равна ускорению свободного падения (прямая горизонтальная линия).
4) Сила тяжести находится по формуле:

F = m ⃗g,

где $m$ – масса.
То есть прямая горизонтальная линия.

Ответ: 21

Ошибка.
Попробуйте повторить позже

Задача 11#20553

Шарик брошен вертикально вверх с начальной скоростью $⃗υ0$ (см. рисунок).

Считая сопротивление воздуха малым, установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять ( $t0$ – время полета). К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Показать ответ и решение

Рассмотрим, как зависят от времени указанные величины.
1) Скорость шарика по вертикали равна:

vy(t)= v0− gt,

где $g$ – ускорение свободного падения.
То есть прямая, направленная вниз (График – А)
2) Проекция ускорения шарика всюду постоянна и равна ускорению свободного падения (прямая горизонтальная линия).
3) Кинетическая энергия шарика равна:

mvy(t)- m- 2 2 2 E кин(t)= 2 = 2 (v0 − 2v0gt+ g t),

то есть парабола с ветвями вверх (График А)
4) Потенциальную энергию можно найти по формуле:

E пот(t)= mgy (t)

Координата $y$ описывается уравнением:

2 y(t)= v0t− gt-, 2

Тогда

( ) Eпот(t)= mg v0t− gt2 2

То есть парабола с ветвями, направленными вниз (График Б)

Ответ: 34

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#64378

Тело равномерно движется по окружности радиусом $R$ . Частота обращения тела равна $ν$ . Установите соответствие между физическими величинами, характеризующими движение тела, и формулами, по которым их можно рассчитать.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбцa и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗ ИЧЕС КИЕ В ЕЛИЧ ИН Ы Ф ОРМ УЛЫ А) линейная скорость 1)2πν 2 2 Б) угловая скорость 2)4π ν R 3)2πR ν 4)-1 ν

Показать ответ и решение

Угловая скорость связана с частотой формулой:

ω = 2πν.

А линейная скорость связана с угловой:

v = ωR = 2πR ν.

Ответ: 31

Ошибка.
Попробуйте повторить позже

Задача 13#64962

Установите соответствие между зависимостью проекции скорости тела от времени (все величины выражены в СИ) и зависимостью координаты этого тела от времени (начальная координата тела равна 0).

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ПРОЕ КЦИ Я СКО РОС ТИ К ООРД ИНА ТА А) vx = −2 1) x= −2t Б) v = 5− t 2) x = −2t2 x 2 3) x = 5t− 0,5t2 4) x =5t+ 2t

Показать ответ и решение

Скорость – это производная от координаты (перемещения) по времени. Из кинематических уравнений:

axt2 ′ x= x0+ v0xt+ --2- vx = (x )= v0x+ axt

Возьмем производную от четырех формул, далее сделаем соответствие:

1) $Sx =− 2t$ , производная от величины в первой степени $(at)′ = a$ , то есть $(− 2t)′ = −2$ .

υx = S′(x)= −2

Ответ – А.

2) $Sx =− 2t2$ , производная от величины во второй степени $(bt2)′ =2bt$ , в нашем случае $− 2t2 = −4t$ .

υ = S′(x)= −4t x

3) $Sx = 5t− 0,5t2$ , производная от величины в первой степени $(at)′ = a$ , то есть $(5t)′ = 5$ , производная от величины во второй степени $2 ′ (bt ) =2bt$ , в нашем случае $2 − 0,5t = −t$ .

υx = S′(x)= 5 − t

Ответ – Б.

4) $Sx =5t+ 2t2$ , производная от величины в первой степени $(at)′ = a$ , то есть $(5t)′ = 5$ , производная от величины во второй степени $(bt2)′ =2bt$ , в нашем случае $2t2 = 4t$ .

υx =S ′(x)= 5+ 4t

Ответ: 13

Ошибка.
Попробуйте повторить позже

Задача 14#65300

Тело, брошенное с горизонтальной поверхности Земли со скоростью $v$ под углом $α$ к горизонту, поднимается на максимальную высоту $h$ над земной поверхностью и затем падает на землю на расстоянии $S$ от места броска. Сопротивлением воздуха пренебречь

Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

Ф изические величины Формулы v2 sin2α А) максимальная высота h над земной поверхностью 1)-2g-- Б ) модуль горизонтальной проекции скорости тела 2) v sinα v2sin2α непосредственно перед падением на землю 3)---g--- 4) vcosα

Показать ответ и решение

А) Найдём проекции начальной скорости $υ$ на оси $Ox$ и $Oy$ :

v0x = vcosα

v0y = vsin α

Так как на тело действует только сила тяжести, то у него есть только вертикальная составляющая ускорения $a = g$ , которое направлено против оси Оу. Значит, зависимости координаты по осям Оу и Ох от времени t в нашем случае будут выглядеть так:

2 y = v⋅tsinα − gt 2

x= v⋅tcosα

Пусть тело достигнет максимальной высоты за $t0$ , то $t0$ равно:

v0sinα 0= v0x − gt0 ⇒ t0 = g

Тогда

2 2 2 2 2 2 H = υ0 ⋅sin-α-− υ0 ⋅sin-α-= υ0 ⋅sin-α-⇒ А – 1 g 2g 2g

Б) Скорость по горизонтали постоянна и равна $v0x = vcosα$

Ответ: 14

Ошибка.
Попробуйте повторить позже

Задача 15#96202

Шарик брошен вертикально вверх с начальной скоростью $⃗v0$ (см. рис.).

Считая сопротивление воздуха малым, установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

|--|---|--| |А-|Б--|В-| -----------

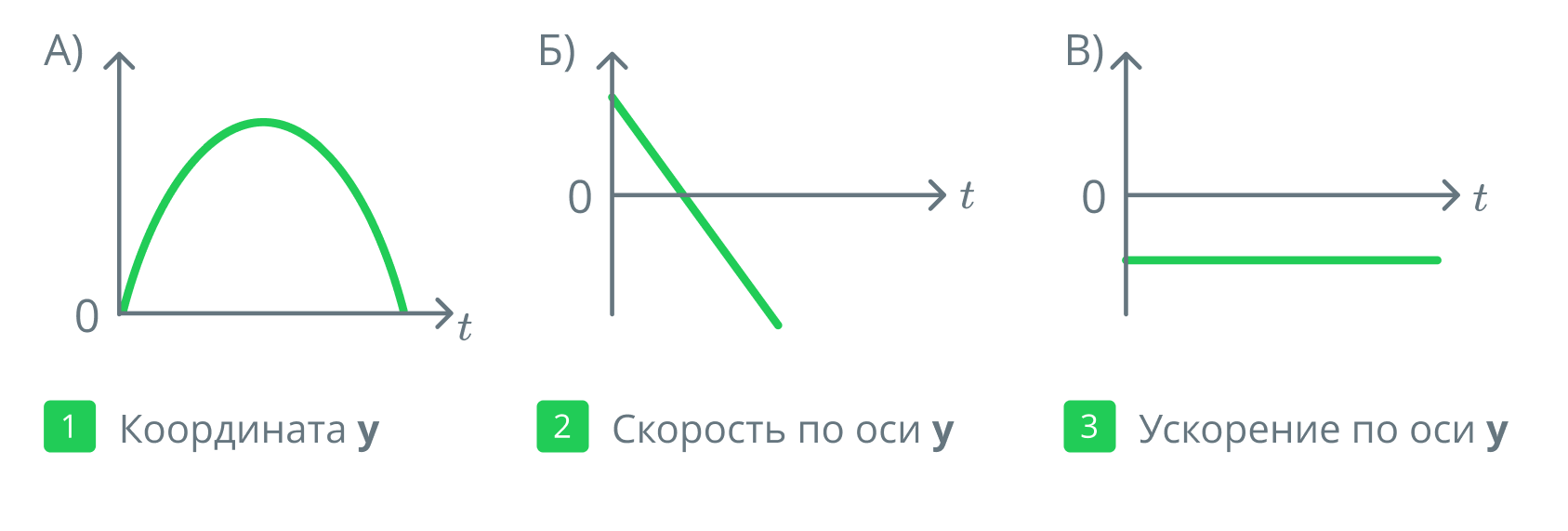
Источники: Школково

Показать ответ и решение

Решение скрыто

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 16#97575

Мячик бросают с начальной скоростью $⃗v0$ под углом $α$ к горизонту с балкона высотой $h$ (см. рисунок).

$PIC$

Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y = 0.
ГРАФИКИ

$PIC$

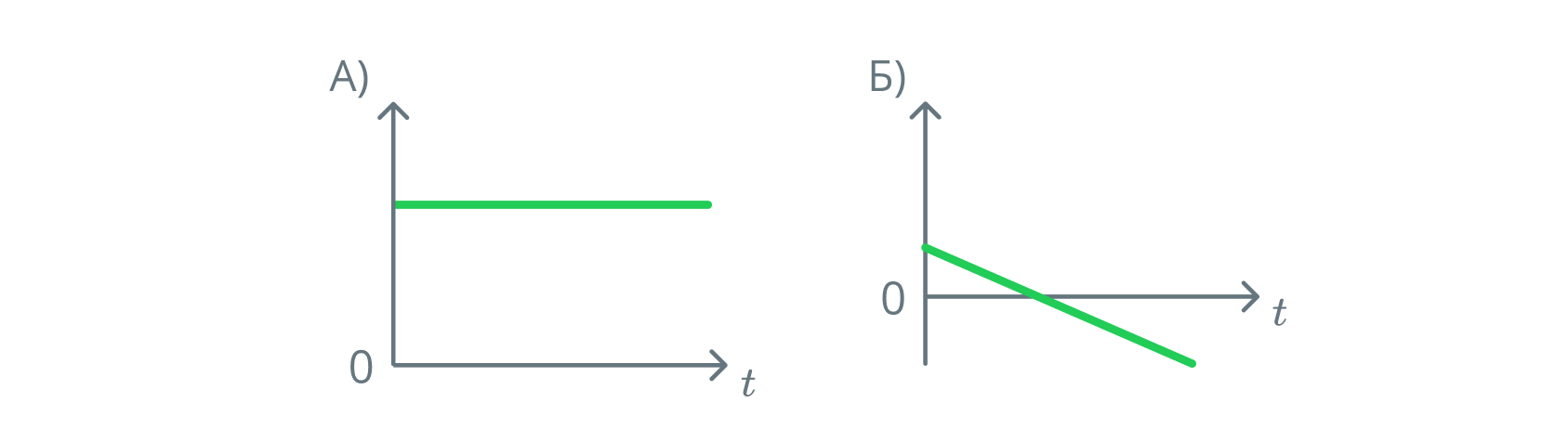
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) координата $x$ мячика
2) проекция импульса мячика на ось $x$
3) проекция импульса мячика на ось $y$
4) потенциальная энергия мячика

Источники: Банк ФИПИ ЕГЭ

Показать ответ и решение

Запишем закон изменения координаты для горизонтальной( $Ox$ ) и вертикальной( $Oy$ ) осей.

( a t2 |{Ox: x= x0 +v0xt+ -x2-- |( ayt2- , Oy: y = y0+ v0yt+ 2

где $v0x$ , $v0y$ - проекции начальных скоростей на горизонтальную и вертикальную оси соответственно;
$ax$ , $ay$ - проекции ускорения на горизонтальную и вертикальную оси соответственно;
$x0$ , $y0$ - начальные координаты мячика по горизонтальной и вертикальную осям соответственно
Найдем эти значения исходя из условий задачи:
Т.к. в нашей задаче на тело, кроме начального броска, не действуют никакие внешние силы, то единственным источником ускорения является гравитационное поле. Тогда т.к. ускорение свободного падения $g$ действуют лишь вертикально вниз, то $ax$ =0, а $ay =− g$ .
Из рисунка видно, что $v0x = v0cosα$ , $v0y = v0sinα$ .
А также $x = 0 0$ и $y = h 0$ . Тогда система для координат будет выглядеть следующим образом: