Тема 19. Задачи на теорию чисел

19.26 Комбинаторика

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела задачи на теорию чисел

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#721

Шесть пчёлок прилетели опылять два разных цветочка. Они договорились, что один цветочек будет опылять ровно одна пчёлка. Им предстоит решить, кому достанутся эти два цветочка на опыление. Сколькими способами они могут распределить двух пчёлок по двум разным цветочкам?

Показать ответ и решение

На первый цветочек может претендовать любая из 6 пчёлок. Как только выбрана пчёлка, которая будет опылять первый цветочек, на второй цветочек может претендовать любая из 5 оставшихся пчёлок.

Какую бы пчёлку не назначили на первый цветочек, после этого назначения остаётся 5 различных возможных вариантов назначить пчёлку на второй цветочек. То есть каждый из 6 вариантов для первого цветочка даёт 5 различных вариантов для второго цветочка.

Получаем, что всего вариантов – “шесть раз по пять”, то есть $6 ⋅ 5 = 30$ .

Ответ:

$30$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#722

Боря выписал все различные делители числа $120$ . Сколько чисел выписал Боря?

Показать ответ и решение

Разложим $120$ на простые множители: $120 = 23 ⋅ 3 ⋅ 5$ . Все делители числа $120$ равны $2a ⋅ 3b ⋅ 5c$ , где

$a$ может принимать значения $0,1,2$ или $3$ ,

$b$ может принимать значения $0$ или $1$ ,

$c$ может принимать значения $0$ или $1$ .

При этом если тройки $(a ,b ,c ) 1 1 1$ и $(a ,b ,c) 2 2 2$ не совпадают, то числа $2a1 ⋅ 3b1 ⋅ 5c1$ и $2a2 ⋅ 3b2 ⋅ 5c2$ – различны.

Таким образом, у числа $120$ столько же различных делителей, сколько существует различных троек вида $(a,b,c)$ , где $a$ принимает одно из четырёх значений, $b$ принимает одно из двух значений, $c$ принимает одно из двух значений, то есть количество подходящих троек равно $4 ⋅ 2 ⋅ 2 = 16$ .

Ответ:

$16$

Ошибка.
Попробуйте повторить позже

Задача 3#723

В честь своего следующего дня рождения Тимур планирует накрыть праздничный стол на себя и шестерых гостей. Тимур хочет сесть во главе стола (его место фиксировано). Он думает, как ему рассадить гостей на шесть одинаковых гостевых стульев (ему не важно, на какой гостевой стул кто сядет, важно лишь кто будет соседями каждого гостя). Сколькими способами он может это сделать?

Показать ответ и решение

Справа от Тимура может сесть любой из 6 гостей. После того, как Тимур определится со своим правым соседом, на место справа от правого соседа Тимура может сесть любой из 5 гостей и т.д.

В итоге сосед, сидящий слева от Тимура будет, определён однозначно, то есть имеется $6! = 720$ вариантов, но не все они различны.

Пусть Тимур зафиксировал гостя, который будет его соседом справа, зафиксировал и его соседа справа и т.д. Он получил некоторую последовательность, в которой он будет сажать гостей, двигаясь в одну сторону вдоль граничной окружности стола.

Но если он будет сажать гостей в той же последовательности, двигаясь в другую сторону вдоль окружности, то при этом для каждого гостя состав его соседей не изменится.

$PIC$

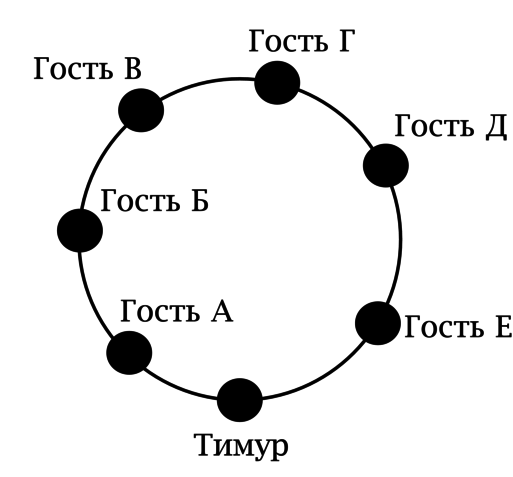
Таким образом, когда мы получили $6!$ вариантов, каждый вариант рассадки мы учли ровно по два раза, следовательно, у Тимура есть $6!= 360 2$ способов рассадить гостей.

Ответ:

$360$

Ошибка.
Попробуйте повторить позже

Задача 4#2016

Боря выписал все различные делители числа $12$ . Сколько чисел выписал Боря?

Показать ответ и решение

Различные делители числа $12$ – это $1$ , $2$ , $3$ , $4$ , $6$ , $12$ , то есть 6 чисел.

Ответ:

$6$

Ошибка.
Попробуйте повторить позже

Задача 5#2017

В честь своего дня рождения Тимур накрыл праздничный стол на себя и шестерых гостей. Тимур хочет сесть во главе стола (его место фиксировано). Он думает, как ему рассадить гостей, ведь у него имеется шесть разных гостевых стульев (которые уже стоят у стола и двигать их он не намерен). Сколькими способами он может это сделать?

Показать ответ и решение

Так как место Тимура за столом фиксировано, то можно считать, что его за столом не будет (ответ от этого не изменится).

Пусть Тимур как-то занумеровал стулья. Тогда на первый стул может претендовать любой из 6 гостей.

Какой бы из 6 гостей не занял первый стул, на второй стул может претендовать любой из оставшихся на этот момент 5 гостей.

...

На последний шестой стул будет претендовать один единственный гость.

В итоге: каждый из 6 вариантов для первого стула даёт пять различных вариантов для второго стула и т.д., то есть всего есть $6! = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 = 720$ различных способов рассадить гостей.

Ответ:

$720$

Ошибка.
Попробуйте повторить позже

Задача 6#2018

Боря выписал все различные делители числа $2016$ . Сколько чисел выписал Боря?

Показать ответ и решение

Разложим $2016$ на простые множители: $2016 = 25 ⋅ 32 ⋅ 7$ . Все делители числа $2016$ равны $2a ⋅ 3b ⋅ 7c$ , где

$a$ может принимать значения $0,1,2$ , $3$ , $4$ или $5$ ,

$b$ может принимать значения $0$ , $1$ или $2$ ,

$c$ может принимать значения $0$ или $1$ .

При этом если тройки $(a ,b ,c ) 1 1 1$ и $(a ,b ,c) 2 2 2$ не совпадают, то числа $2a1 ⋅ 3b1 ⋅ 7c1$ и $2a2 ⋅ 3b2 ⋅ 7c2$ – различны.

Таким образом, у числа $2016$ столько же различных делителей, сколько существует различных троек вида $(a,b,c)$ , где $a$ принимает одно из шести значений, $b$ принимает одно из трёх значений, $c$ принимает одно из двух значений, то есть количество подходящих троек равно $6 ⋅ 3 ⋅ 2 = 36$ .

Ответ:

$36$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#2019

Белоснежка и семь гномов садятся за круглый стол. Известно, что Ворчун не хочет сидеть рядом с Весельчаком и Соней. Сколькими способами их можно рассадить за стол так, чтобы Ворчуна всё устраивало, если считать, что не важно, кто на какое место сядет, важно только, кто будет соседями каждого гнома и Белоснежки?

Показать ответ и решение

Ответ не зависит от того, в каком порядке мы будем сажать Белоснежку и гномов за стол. Пусть первым за стол садится всегда Ворчун. Тогда его правым соседом может быть один из 5 кандидатов. После того, как его правый сосед выбран, на роль левого соседа Ворчуна могут претендовать 4 кандидата.

Далее имеем ситуацию как на рисунке:

$PIC$

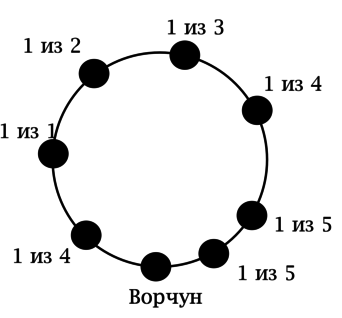
Таким образом, есть $1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 4 ⋅ 5 ⋅ 5 = 2400$ способов, но не все они различны. На самом деле каждый способ мы учли по два раза (если рассаживать кандидатов по часовой стрелке в определённой последовательности и если рассаживать их против часовой стрелки в той же последовательности, то рассадки будут одинаковыми).

В итоге есть $2400 : 2 = 1200$ способов, которыми можно рассадить за стол гномов и Белоснежку так, чтобы Ворчуна всё устроило.

Ответ:

$1200$

Ошибка.
Попробуйте повторить позже

Задача 8#2020

Даны два числа $N = p1k1 ⋅ ⋅⋅⋅ ⋅ pnkn$ и $M = N ⋅ pi$ , где $p1,...,pn$ – простые числа, $i$ – некоторое число из множества ${1,2,...,n }$ . Во сколько раз количество различных делителей числа $M$ больше, чем количество различных делителей числа $N$ ?

Показать ответ и решение

Все делители числа $N$ равны $p1a1 ⋅ ⋅⋅⋅ ⋅ pnan$ , где
$a1$ принимает одно из $k1 + 1$ значений (возможные значения: $0$ , $1$ , ..., $k1$ )

...

$a n$ принимает одно из $kn + 1$ значений.

При этом, если упорядоченные наборы $(b1,...,bn)$ и $(c1,...,cn)$ не совпадают, то числа $p1b1 ⋅ ⋅⋅⋅ ⋅ pnbn$ и $p1c1 ⋅ ⋅⋅⋅ ⋅ pncn$ – различны.

Таким образом, у числа $N$ столько же различных делителей, сколько существует различных упорядоченных наборов вида $(a1,...,an)$ , где $a1$ принимает одно из $k1 + 1$ значений, $...$ , $an$ принимает одно из $kn + 1$ значений, то есть количество подходящих наборов равно $(k1 + 1) ⋅ ⋅⋅⋅ ⋅ (ki + 1) ⋅ ⋅⋅⋅ ⋅ (kn + 1)$ .