18.23 Графика. Функции с модулем: корыто и другие
Ошибка.
Попробуйте повторить позже
При каких положительных значениях параметра уравнение
имеет решения?
Обозначим
Для положительных выполняется
тогда возможны три случая раскрытия модулей:
- 1.
-
- 2.
-
- 3.
-
Резюмируя, получим
Это «корыто» с ветвями вверх, дно которого лежит на горизонтальной прямой
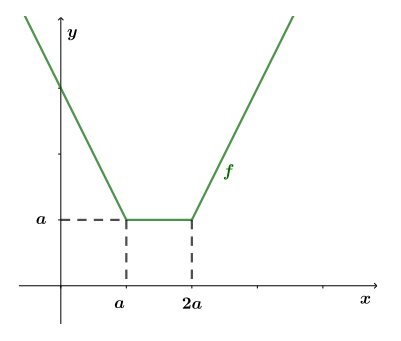
В правой части уравнения имеем константу ей соответствует горизонтальная прямая
Очевидно, что если
эта прямая проходит не ниже дна корыта, то уравнение имеет решения. Тогда имеем:
Пересекая с условием, что положительно, получаем
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Выполнен обоснованный переход к неравенству, которое может отличаться от верного знаком неравенства | 2 |
| ИЛИ | |
| Неравенство составлено верно, но допущена ошибка в его решении | |
| Верно сведено к исследованию графически или аналитически | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
При каких значениях параметра уравнение
имеет ровно одно решение?
Обозначим
Возможны три случая раскрытия модулей в левой части, поскольку первый модуль меняет знак в точке второй — в
точке
- 1.
-
- 2.
-
- 3.
-
Резюмируя, получим
Это «корыто» с ветвями вверх, дно которого лежит на наклонной прямой
Правая часть задает пучок прямых, проходящих через точку так как
независимо от выбора
При этом
как обычно вертикальная прямая не входит в пучок.
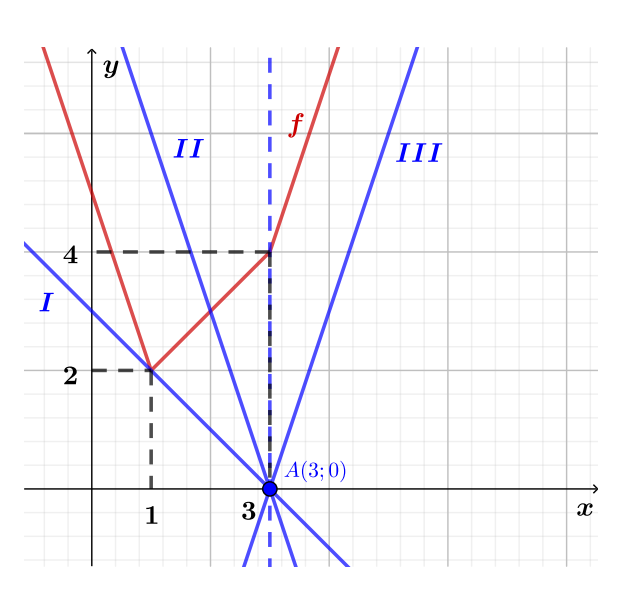
-
В положении
прямая пучка проходит через левый угол корыта — точку
- В положении
прямая пучка параллельна левой ветке корыта
а значит, их угловые коэффициенты равны
- В положении
прямая пучка параллельна правой ветке корыта
а значит, их угловые коэффициенты равны
Видим, что прямая пучка имеет ровно одно пересечение с корытом в положении а также между положениями
и
включая
и не включая
за исключением вертикальной прямой.
Переходя к угловым коэффициентам, получаем
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Ответ отличается от
верного невключением либо | 3 |
| ИЛИ | |
| Недостаточное обоснование построения | |
| Рассмотрены верно два из трёх взаимных
расположений графиков функций с
верным нахождением значений параметра
| 2 |
| Верное сведение к исследованию
графически или аналитически, при этом
может быть верно найдено хотя бы одно
из значений параметра | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
При каких значениях параметра уравнение
имеет бесконечно много решений?
Рассмотрим уравнение левой части раскроем модули и представим ее в кусочном виде:
Это «корыто» с углами в точках и
Построим его график.
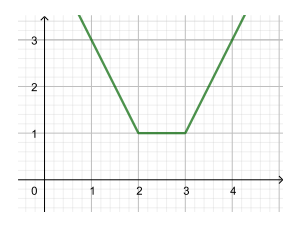
Уравнение правой части задает произвольную горизонтальную прямую. Единственный случай, в котором эта прямая
имеет с корытом бесконечное количество точек пересечения, достигается при
когда горизонтальная прямая содержит
отрезок дна корыта.
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Верно найдено значение | 2 |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения при которых система
имеет единственное решение.
Пусть Тогда
График — это «корыто» с изломами в точках
и
График
— это уголок модуля с
вершиной в точке
График
получается из графика
сдвигом по вертикали на
Изобразим графики
функций
и те положения графика
при которых графики
и
будут иметь единственную точку
пересечения.
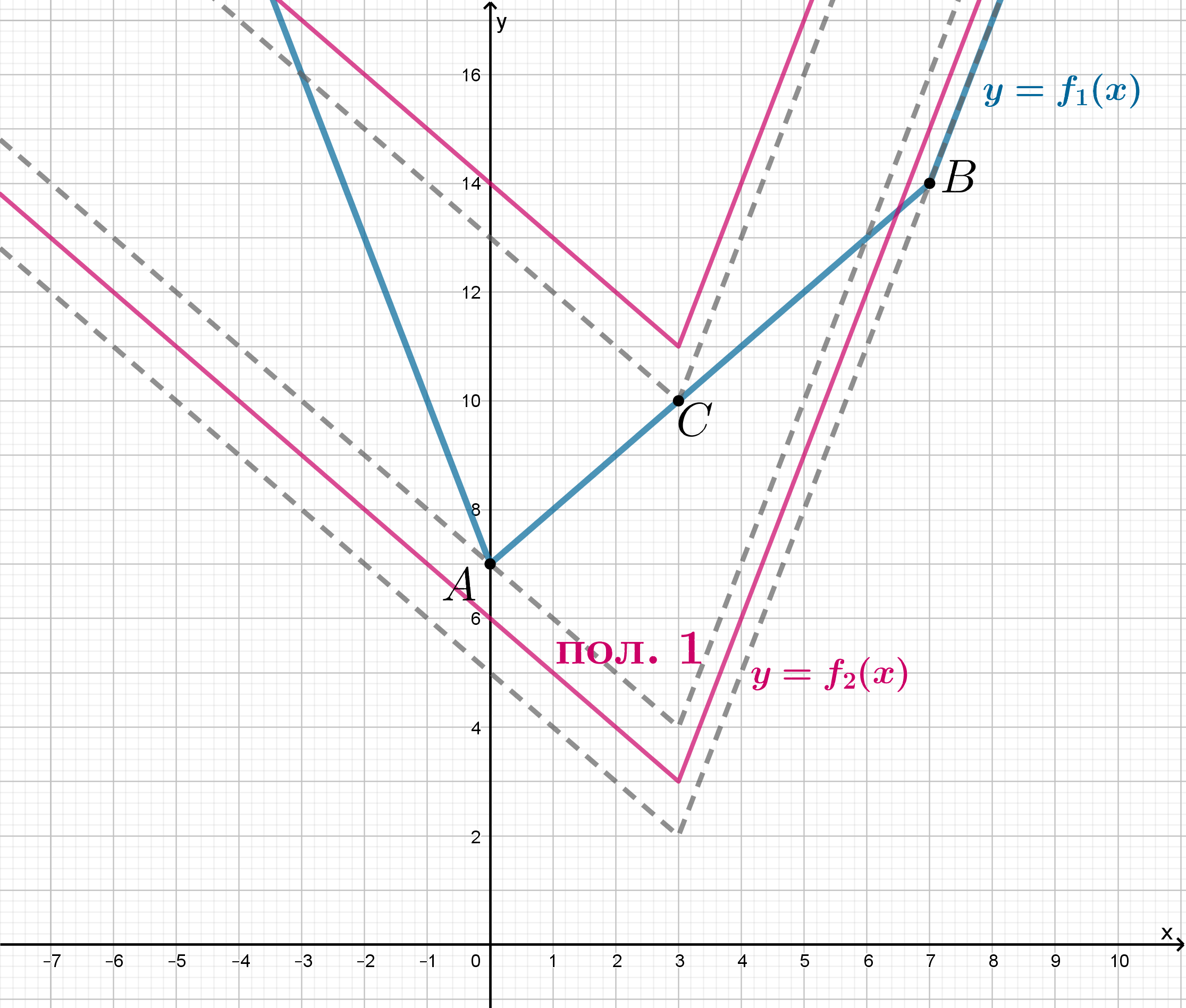
При график
будет находиться в положении 1. Чтобы убедиться в этом, достаточно найти точку пересечения
оси ординат с левой веткой
и понять, что эта точка находится ниже точки
При этом точка
на правой ветке
с абсциссой
будет находиться выше точки
а именно иметь ординату
Если менять значение от
до
то график
будет двигаться снизу вверх, причем сначала он пройдет
через точку
затем через точку
Все положения графика
между прохождениями через эти точки, не
включая сами прохождения, нас устраивают, так как мы будем иметь одну точку пересечения графиков
и
Далее, двигаясь от точки к точке
график
будет иметь 3 точки пересечения с графиком
, что нам не подходит.
Строго выше положения, когда график
проходит через точку
мы будем иметь одну точку пересечения графиков
и
, что нам подходит. При этом координаты точки
ищутся как координаты точки на отрезке прямой
абсцисса
которой равна абсциссе вершины
графика
Найдем значения параметра, соотвествующие прохождению графика через точки
Тогда исходная система имеет единственное решение при
Ошибка.
Попробуйте повторить позже
Исследуйте траекторию движения графиков функций, записанных в системе
и определите, при каких система имеет бесконечное множество решений.
Обозначим ,
.
- 1)
- Ищем траектории движения графиков.
График
представляет собой “корыто с кривым дном”, а при равенстве нулей подмодульных выражений (при
) уголок. Боковые ветви корыта имеют вид
,
.
Чтобы найти траекторию движения этого графика, можно следить за любой его точкой, например, за точкой
. Следовательно, корыто движется по кривой
.
График
представляет собой уголок, ветви которого имеют вид
,
.
Чтобы найти траекторию движения уголка, можно следить за его вершиной
. Значит, уголок движется по прямой
- 2)
- Определяем, при каком
число решений системы бесконечно.
Заметим, что левая ветвь корыта с левая ветвь уголка параллельны, так как имеют одинаковый коэффициент перед
. То же можно скапзать про их правые ветви. Бесконечное множество решений у системы будет, если корыто и уголок будут иметь бесконечно много точек пересечения, что происходит только в тех случаях, когда одна из боковых ветвей одного графика накладывается на боковую ветвь другого. Это значит, что уравнения, задающие прямые, на которых расположены эти ветви, одинаковы.
Следовательно,
Схематично это выглядит так:
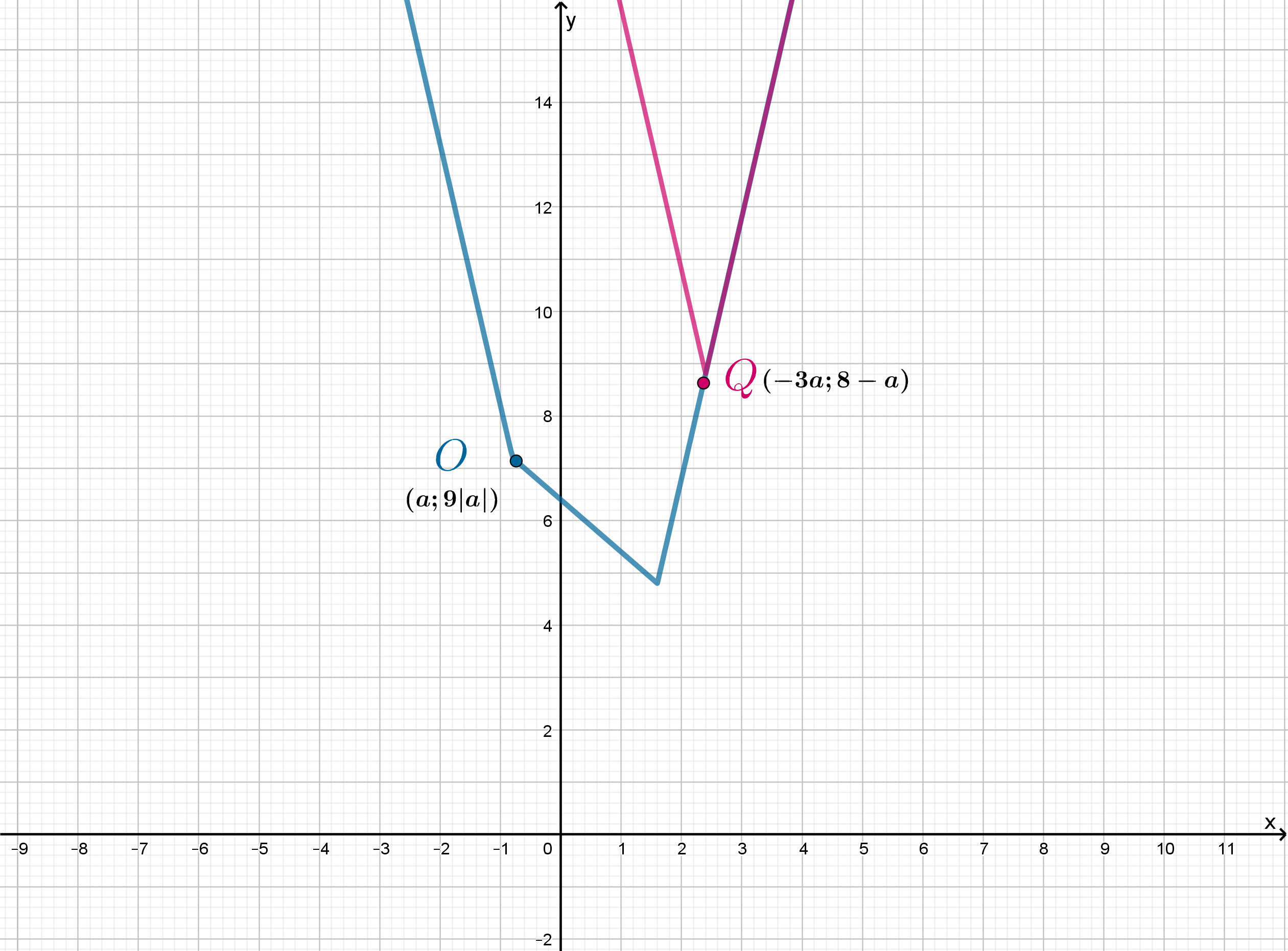
Ошибка.
Попробуйте повторить позже
Найдите , при которых уравнение
Сделаем замену , получим
В левой части имеем корыто, значит, левая чаcть будет равна 2 при , т.к. дно корыта принадлежит
горизонтальной прямой
.
![]()
Нам нужно найти такие значения , при которых существует хотя бы одно значение
такое, что
. Это
равносильно нахождению таких
, при которых двойное неравенство
- При
наше двойное неравенство равносильно системе
Решения есть, значит,
подходит.
- При
, поделив все части неравенства на
, получим
Заметим, что
как сумма взаимно обратных дробей, причем равенство будет достигаться для
при любом
. Тогда при любом
, для которого
будет решением (возможно решений будет больше, но нам важно, что как минимум одно точно есть), если же
и
будет выполняться
Объединив, получим ответ .
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых уравнение
имеет бесконечно много решений.
Рассмотрим левую часть как функцию от
Графиком
этого уравнения является корыто. Раскроем модули:
Графиком правой части является горизонтальная прямая.
Необходимо, чтобы эта горизонтальная прямая имела бесконечно много общих
точек с корытом. Изобразим график корыта:
Следовательно, горизонтальная прямая должна проходить через дно корыта, следовательно,
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Выполнен необоснованный переход к результату | 2 |
| Верно сведено к исследованию графически или аналитически | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых уравнение
имеет единственное решение.
Пусть
Тогда функция
задает корыто с наклонным дном:
Функция задает пучок прямых, проходящих через точку
Необходимо, чтобы прямая из пучка прямых имела ровно одну общую точку с
корытом.
Изобразим графики:
Опишем ситуации 1,2 и 3. Пусть тогда
прямая
параллельна правой ветви
корыта, тогда
решений нет. Но при
мы имеем одну точку пересечения (как раз с
правой ветвью корыта). Если
параллельна
то
следовательно, при
— одно решение. Тогда
откуда
прямая
проходит через точку
Следовательно, откуда
— при этом
имеем одну точку
пересечения.
прямая
параллельна левой ветви
корыта, тогда
решение есть. Также при
есть единственное решение. Следовательно,
откуда при
то есть при
имеем одну точку
пересечения.
Следовательно, ответ
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С
помощью верного рассуждения получены
все значения | 3 |
| С помощью верного рассуждения
получены не все значения | 2 |
| Задача верно сведена к исследованию взаимного расположения графика функции и прямой (аналитически или графически). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых уравнение
имеет единственное решение.
Перепишем уравнение в виде
Пусть
Тогда первое уравнение задает
параболу
часть которой, находящаяся под осью абсцисс, отражена
наверх. Второе уравнение задает пучок прямых, проходящих через точку
Изобразим положения прямой из пучка прямых, при которых она имеет ровно
одну общую точку с графиком
Положение 1: прямая касается правой ветви параболы:
Тогда уравнение
имеет единственное решение, следовательно, его дискриминант равен нулю:
Нам подходит так как при
прямая касается несуществующей на
графике
части параболы (при
).
Положение 2: прямая проходит через точку
Следовательно, ответ:
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Верно исследовано одно из двух положений | 2 |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых система
имеет единственное решение.
Пусть
Тогда
Тогда график функции получаем сдвигом графика
функции
вертикально на
единиц (вверх/вниз). Необходимо, чтобы
график функции
(корыто с наклонным дном) и график функции
(уголок) имели одну общую точку.
Изобразим графики:
Одно решение система имеет, когда правая ветвь уголка
проходит через точку
Заметим, что правая ветвь уголка не параллельна правой ветви корыта,
следовательно, при они пересекаются, то есть всегда дают одну общую
точку. На рисунке изображены другие положения уголка относительно корыта,
при которых количество общих точек равно 0, 2, 3 или 4.
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Выполнен необоснованный переход к результату | 2 |
| Верно сведено к исследованию графически или аналитически | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |



