03 Нахождение длин отрезков
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
— медиана,
Найдите
Источники:
Медиана, проведенная к стороне, делит эту сторону пополам, то есть
![]()
Ошибка.
Попробуйте повторить позже
Сторона равностороннего треугольника равна Найдите биссектрису этого
треугольника.
Источники:
Заметим, что биссектриса равностороннего треугольника совпадает с медианой и
высотой. Опустим высоту из на
Получим прямоугольный треугольник
По теореме пифагора для
Получим
Тогда мы получили, что длина медианы равна 18, но тогда и длина биссектрисы равна 18.
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
— медиана,
Найдите
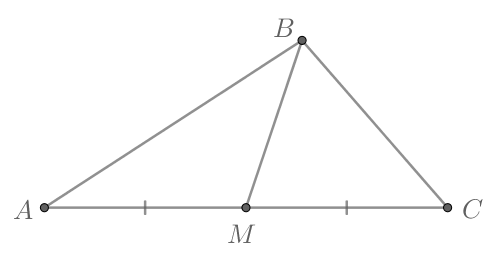
Так как — медиана, то
Ошибка.
Попробуйте повторить позже
Точки и
являются серединами сторон
и
треугольника
соответственно. Отрезки
и
пересекаются в точке
Найдите
Так как и
— середины сторон
и
то
и
— медианы, которые по условию пересекаюся в точке
Точкой пересечения медианы делятся в отношении
считая от вершины, то есть
Тогда
и при этом
то есть
Отсюда получаем, что
![]()
Ошибка.
Попробуйте повторить позже
Точка и
являются серединами сторон
и
треугольника
соответственно. Отрезки
и
пересекаются в точке
Найдите
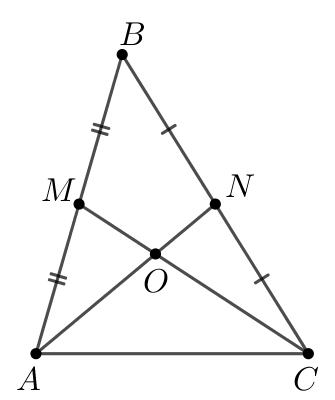
и
— медианы треугольника
Так как медианы треугольника
пересекаются в одной точке и точкой пересечения делятся в отношении
считая от вершины, то
Ошибка.
Попробуйте повторить позже
Точки и
являются серединами сторон
и
треугольника
соответственно. Отрезки
и
пересекаются в точке
Найдите
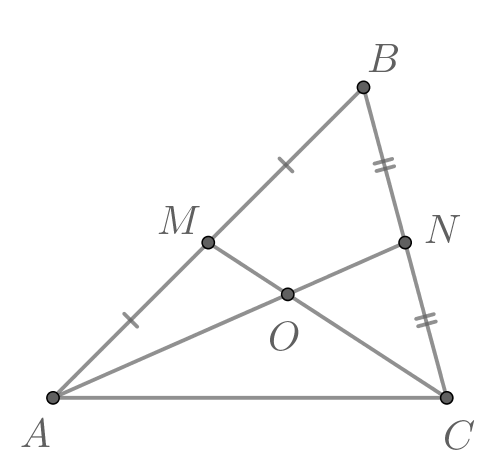
Медианы треугольника пересекаются в одной точке и точкой пересечения делятся
в отношении считая от вершины. Тогда
Ошибка.
Попробуйте повторить позже
Прямая, параллельная стороне треугольника
пересекает стороны
и
в точках
и
соответственно,
Найдите
параллельна
то есть треугольники
и
подобны (так как два угла при параллельных прямых равны).
Тогда из подобия,
то есть
Тогда
![]()
Ошибка.
Попробуйте повторить позже
Точки и
являются серединами сторон
и
треугольника
сторона
равна 57, сторона
равна 74, сторона
равна 48. Найдите

— средняя линия. По свойству средней линии
Ошибка.
Попробуйте повторить позже
Прямая перпендикулярная медиане
треугольника
делит её пополам. Найдите сторону
если сторона
равна 38.
Обозначим точку пересечения и
за
Тогда
перпендикулярна
и делит её пополам, т.е. в треугольнике
— медиана и высота, т.е. треугольник
— равнобедренный,
— медиана треугольника
т.е.
Отсюда получаем, что
![]()


