01 Термодинамика процесса - Каталог заданий по Олимпиадной физике в Школково

Ошибка.
Попробуйте повторить позже

Задача 41#120192Максимум баллов за задание: 10

Девочка шла по улице зимой с воздушным шариком, надутым гелием. Температура воздуха на улице была равна $t1 = − 13∘C,$ а шарик имел при этом объём $V1 = 5 л.$ Девочка пришла домой, где температура воздуха равна $t2 = 27∘C.$ Гелий – одноатомный газ, который в данной задаче можно считать идеальным. Атмосферное давление $P = 1 атм. 0$ Упругостью оболочки можно пренебречь.
1. Какой объём примет шарик? Ответ выразите в литрах и округлите до сотых.
2. Какое количество теплоты получит гелий из окружающей среды? Ответ выразите в $Дж$ и округлите до целых.

(МОШ, 2019, 11)

Источники: МОШ, 2019, 11

Показать ответ и решение

Т.к. давление на улице в комнате и на улице одинаковое, то процесс можно считать изобарным:

V1 T1 T2 300 V2 = T2 ⇒ V2 = V1T1 = 5260 = 5,77л

Запишем первое начало термодинамики:

Q = ΔU + A

Q = CPνΔT = CPν (T2 − T1)

Количество вещества найдём из уравнения состояния:

P V = νRT ⇒ ν = P0V1- 0 1 1 RT1

Подставляем в первое начало термодинамики:

5 P0V1 Q = 2 -T--(T2 − T1) = 192Дж 1

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 42#120367Максимум баллов за задание: 10

При охлаждении одного моля гелия от начальной температуры $T0$ до некоторой конечной температуры $Tx$ в процессе с теплоёмкостью $C,$ прямо пропорциональной температуре $T,$ газ совершил работу, равную нулю. В самом начале процесса охлаждения давление газа изменялось прямо пропорционально его объёму. Найдите величину положительной работы газа в данном процессе и отношение $Tx∕T0.$

(Всеросс., 2014, ЗЭ, 10)

Источники: Всеросс., 2014, финал, 10

Показать ответ и решение

Решение скрыто

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 43#120369Максимум баллов за задание: 10

При охлаждении одного моля гелия от начальной температуры $T0$ до некоторой конечной температуры $Tx$ в процессе с теплоёмкостью $C,$ прямо пропорциональной температуре $T,$ газ совершил работу, равную нулю. В самом начале процесса охлаждения давление газа изменялось прямо пропорционально его объёму. Найдите величину положительной работы газа в данном процессе и отношение $Tx∕T0.$
(Всеросс., 2014, ЗЭ, 10)

Источники: Всеросс., 2014, ЗЭ, 10

Показать ответ и решение

Решение скрыто

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 44#120370Максимум баллов за задание: 10

В сосуде находятся гелий $He$ и азот $N2$ в количестве $ν1$ и $ν2$ соответственно. Сосуд разделён на две части пористой перегородкой $П$ (рис.), которая свободно пропускает гелий и не пропускает азот, причём изначально азот был только в правой части. Пренебрегая теплоёмкостью стенок сосуда и поршней, найдите теплоёмкость системы при нагревании в следующих условиях:
1) при закреплённых поршнях;
2) при свободных поршнях, создающих постоянные давления;
3) при свободном левом поршне, создающем постоянное давление, и закреплённом правом поршне.
Универсальная газовая постоянная $R$ известна.

(Всеросс., 2005, ЗЭ, 10)

$PIC$

Источники: Всеросс., 2005, ЗЭ, 10

Показать ответ и решение

Решение скрыто

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 45#125169Максимум баллов за задание: 10

Правое колено пневматического пресса диаметром $d = 5$ см перекрыто лёгким плотно пригнанным поршнем, лежащим на упорах. На поршень положили груз массой $m = 5$ кг. После этого левое колено закрыли лёгким поршнем, так, что давление воздуха в цилиндрах осталось равным нормальному атмосферному давлению $p = 100kПа 0$ , а его объём равным $V0 = 22л$ . Какую минимальную работу $Amin$ необходимо совершить, чтобы, двигая левый поршень, поднять груз в правом колене на высоту $x = 10 см$ . Утечкой газа, трением поршней о стенки цилиндров и теплоёмкостью пресса можно пренебречь. Считать, что воздух в прессе теплоизолирован. Уравнение адиабатного процесса для воздуха имеет вид $1,4 pV = const$ .

$PIC$

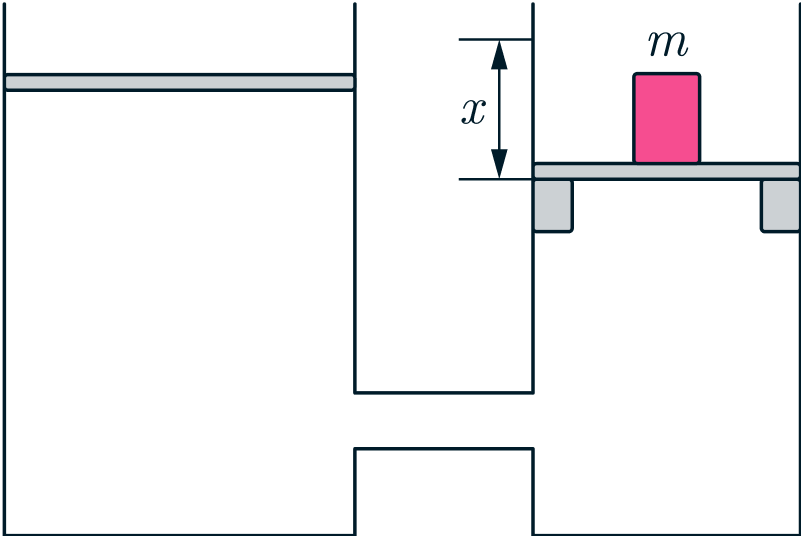
(Курчатов 2025, 11)

Показать ответ и решение

Для того, чтобы поднять груз, первоначально необходимо довести давление газа до величины:

4mg P1 = P0 +---2 , πd

где $πd2- 4$ - площадь поршня в правом колене пресса. Работа, которая будет совершена при этом равна изменению внутренней энергии газа, так как при адиабатическом процессе теплообмен отсутствует. Используя заданное уравнение процесса и уравнение состояния идеального газа, запишем уравнение адиабатического процесса «в координатах $T P$ »:

PV γ = const; PV--= const;⇒ T P1−γγ = const T

Вычислим изменение температуры газа:

[( ) γ−γ1 ] ΔT = T0 1 + 4mg--- − 1 πd2P0

Работа, совершенная над газом на этом этапе, равна изменению внутренней энергии и вычисляется по формуле:

5 A1 = ΔU = 2νR ΔT

После того, как давление газа достигло значения $P1$ , груз начнет подниматься, при этом давление, объем и температура газа изменяться не будут, поэтому совершенная работа будет равна изменению потенциальной энергии груза $A2 = mgx$ . Таким образом, полная работа по поднятию груза в правом колене рассчитывается по формуле:

[( ) γ−1- ] A = A1 + A2 = 5νRT0 1 + 4mg--- γ − 1 + mgx = 2 πd2P0

[( )γ−1 ] = 5P V 1+ -4mg-- γ − 1 + mgx ≈ 360Д ж 2 0 0 πd2P0

Заметим, что основной вклад дает первое слагаемое, то есть работа, совершенная при неподвижном грузе.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 46#125288Максимум баллов за задание: 10

Сосуд постоянного объёма $V1$ соединён короткой трубкой с краном $K$ с длинным горизонтальным цилиндром, в котором может свободно двигаться поршень. Правый торец цилиндра открыт в атмосферу, давление которой $P0$ постоянно. В начальном состоянии кран закрыт, поршень прижат силой атмосферного давления к левому торцу цилиндра, в сосуде находится гелий при температуре $T1 = 300К$ и давлении $P1 = kP0$ , где $k = 4$ . Кран открывают, гелий перетекает в цилиндр, и вся система переходит в новое состояние равновесия. Считая, что все стенки, поршень и трубка с краном не проводят тепло, найдите следующие величины:

Конечную температуру гелия $T2$ .
Отношение $ΔVV1-$ , где $ΔV$ — приращение объёма гелия (конечный объём гелия в цилиндре).

Примечание: объём трубки с краном не учитывайте.

$PIC$

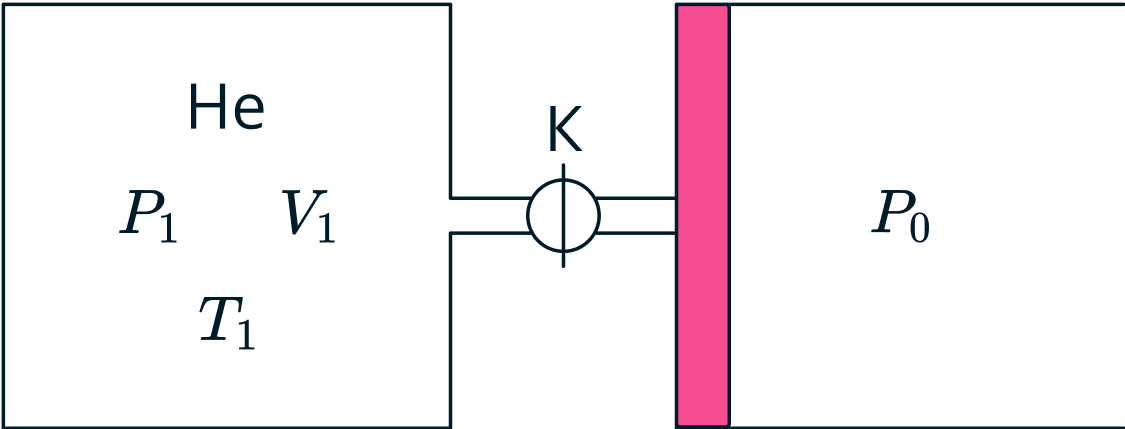
(Курчатов 2025, 10)

Показать ответ и решение

Пусть $ν$ — число молей газа, $S$ и $x$ — площадь и перемещение поршня. Согласно первому началу термодинамики имеем:

0 = νCV (T2 − T1)+ A,

$CV$ — молярная теплоёмкость при постоянном объёме, $A$ — работа газа.

$PIC$

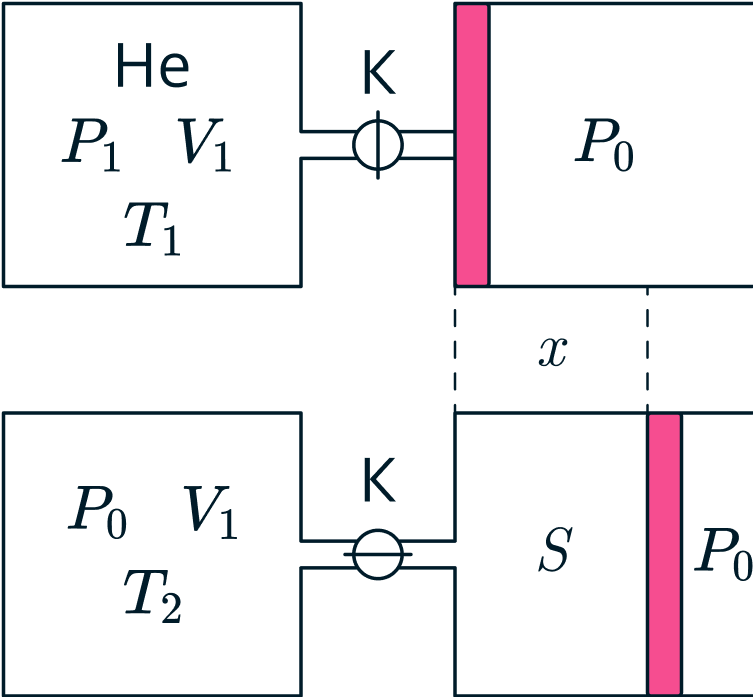
Запишем уравнение баланса энергии для поршня:

0 = A − P0Sx.

Нуль в левой части — приращение механической энергии поршня (энергия не изменилась). Второе слагаемое в правой части представляет собой работу постоянной силы атмосферного давления $P0S$ на перемещении $x$ . Эта работа отрицательна, так как направление действия силы давления противоположно направлению перемещения. Получаем:

A = P0Sx.

Выразим работу $A$ через начальную и конечную температуры газа. Для этого воспользуемся уравнением состояния:

P1V1 = νRT1,

P0(V1 + Sx ) = νRT2 → P0V1 + A = νRT2.

Полагая в первом уравнении $P1 = kP0$ , получаем:

νRT1 νRT1 P0V1 =--k--, A = νRT2 − --k--.

Подставляя этот результат в уравнение первого начала термодинамики, находим конечную температуру газа:

νRT1- kCV-+-R- 0 = νCV T2 − νCV T1 + νRT2 − k → T2 = T1 kCP ,

$CP = CV + R$ — молярная теплоёмкость при постоянном давлении.

Для того чтобы найти приращение объёма газа, воспользуемся найденными выше выражениями для работы $A$ :

( ) ΔV = Sx = A--= νR- T − T1 . P0 P0 2 k

Отношение $ΔV∕V1$ равно:

( ) ( ) ΔV-= νR--- T2 − T1 = k- T2 − T1 = kT2-− 1. V1 P0V1 k T1 k T1

Используя выражение для $T2$ , этот результат можно привести к следующему виду:

ΔV k− 1 ----= ----, V1 γ

$γ = CP∕CV$ — показатель адиабаты.

Упростим полученные формулы для одноатомного газа. В этом случае $CV = 32R$ , $CP = 5R2$ , $γ = 53$ ,

3k+ 2 ΔV 3(k − 1) T2 = T1------= 210К, ----= -------= 1,8. 5k V1 5

Следует отметить, что в данной задаче нельзя пользоваться уравнением адиабаты, поскольку рассматриваемый процесс является необратимым.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 47#126716Максимум баллов за задание: 10

Газообразный гелий сжимается в процессе $1 − 2$ с постоянной молярной теплоёмкостью $C = 0,5R.$ Затем газ расширяется в процессе $2− 3,$ в котором давление прямо пропорционально объёму (см. рис.). В процессе $2 − 3$ к газу подводят количество теплоты $Q.$ Работа внешних сил над газом при сжатии и работа газа при расширении равны.
1) Найти работу $A$ внешних сил над газом при сжатии.
2) Какое количество $Q12$ теплоты (с учётом знака) получил газ в процессе $1− 2$ ?

(«Физтех», 2018, 11)

$PIC$

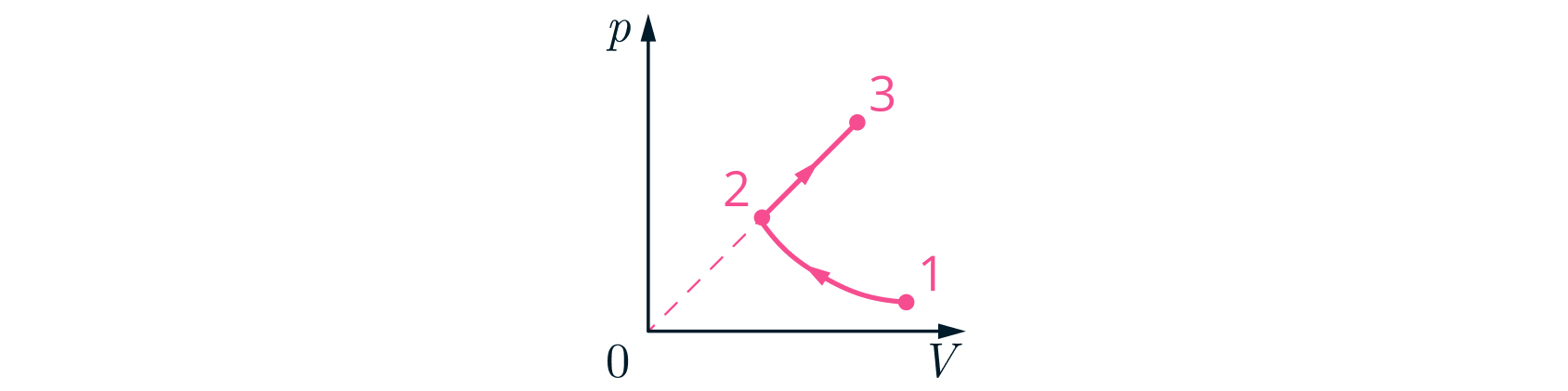
Источники: «Физтех», 2018, 11

Показать ответ и решение

Решение скрыто

Ответ: