Тема СТЕРЕОМЕТРИЯ

Счёт отрезков в стерео

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела стереометрия

Разделы подтемы Счёт отрезков в стерео

Теорема косинусов, теорема Пифагора, использование теоремы о трёх перпендикулярах

Отношение отрезков в стерео: подобие, Фалес, Менелай

Случаи расположения точек

Расстояние между скрещивающимися

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#80774

В основании призмы лежит равносторонний треугольник площади 1. Площади её боковых граней равны 3, 3 и 2. Найдите объём призмы.

Источники: Физтех - 2024, 11.7 (см. olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Во-первых, надо осознать картинку. Она, как будто, симметричная, но не стоит так думать сразу. Давайте опустим высоты из точки A_1 на прямые AB, AC, и плоскость ABC. Что тогда можно заметить? Какие принципиально разные случаи есть падения высоты на плоскость ABC?

Подсказка 2

Есть два случая - падение во внутрь призмы и во вне. Однако, при всем этом, у нас расстояния от точки A_1’(основание высоты) до прямых AB и AC равны, в силу равенства прямоугольных треугольников. Как тогда можно равносильно переформулировать случаи, когда высота падает во внутрь, а когда наружу? Как связать это с равноудаленностью от сторон?

Подсказка 3

Все верно, либо точка основания высоты лежит на внешней биссектрисе, либо на внутренней(угла BAC). Давайте посмотрим на второй случай. Мы видим, что прямые AA’ и A_1A’ перпендикулярны BC. Что тогда это значит? Чем это хорошо в нашей картинке?

Подсказка 4

Тем, что тогда BB_1 перпендикулярен BC, а значит BB_1C_1C - прямоугольник. Но тогда, если сторона треугольника в основании равна а, выходит, что a * AA_1 = 2, a * A_1K = 3. Тогда, пришли к противоречию, так как A_1K > AA_1. Значит, остался второй случай. Если прямая внутренней биссектрисы, была перпендикулярна прямой BC, то внешняя биссектриса будет…

Подсказка 5

Параллельна! А тогда, высота в параллелограмме CC_1B_1B - высота призмы. Значит, остается найти C_1H. Ну, а это уже чисто дело техники(и нескольких теорем Пифагора).

Показать ответ и решение

Если бы призма была прямая, то площади боковых граней были бы равны. Значит, призма наклонная.

Обозначим призму $ABCA1B1C1,$ площади из условия $SAA1B1B = SAA1C1C = 3.$

Пусть $A1K, A1M$ — высоты параллелограммов $AA1B1B$ и $AA1C1C.$ Тогда $A1K = A1M,$ т.к. площади равны, а также равны их основания, так как равносторонний треугольник.

Пусть $′ A$ — проекция $A1$ на плоскость $ABC.$ Тогда $′ ′ A K = AM,$ следовательно, точка равноудалена от прямых $AB$ и $AC.$

(a) Рассмотрим случай, когда $′ A$ принадлежит биссектрисе $AL$ угла $∠ABC.$ $AL$ — высота, медиана и биссектриса в равностороннем треугольнике.

$PIC$

AL ⊥ BC } ′ A1A′ ⊥ BC =⇒ BC ⊥(AA1A ) =⇒ BC ⊥ AA1 =⇒ BC ⊥ BB1

Тогда получаем, что $BB1C1C$ — прямоугольник. Пусть сторона треугольника $ABC$ равна $a.$ Посчитаем площадь прямоугольника и параллелограмма.

S1 =a ⋅AA1, S2 = a⋅A1K

2 =a ⋅AA1, 3= a⋅A1K

Но $A1K < AA1,$ тогда

3= a⋅A1K < a⋅AA1 = 2

получаем противоречие.

(b) Рассмотрим случай, когда $A′$ принадлежит внешней биссектрисе $AL$ угла $∠ABC.$

$PIC$

AA′ ∥BC )|} A1A∥BB1 =⇒ (AA1A′) ∥(BB1C ) AA′ ∥BC |)

Но $(AA1A′)⊥(ABC ),$ следовательно, $(BB1C)⊥ (ABC ),$ откуда следует, что высота $CH1$ параллелограмма $CC1B1B$ совпадает с высотой призмы $(C1H = A1A′).$ В итоге

V = SABC ⋅CH1 = 4√3

Ответ:

$√43-$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#81377

Длина ребра куба $ABCDA ′B′C′D′$ равна 1. Найдите радиус сферы, проходящей через точку $B$ и касающейся прямых $AD,AA′$ и $′ ′ A B$ .

Источники: Миссия выполнима - 2024, 11.4 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Тут у нас и параллельные прямые, и биссектрисса - давайте поищем равные углы. Помним, что биссектрисса отсекает от параллелограмма равнобедренный треугольник.

Подсказка 2

Верно, получаем MCK равнобедренный. Тогда ОС (где О - центр окружности) - серединный перпендикуляр КМ, а треугольники KOC и МОС равны и равнобедренны. На этом этапе давайте остановимся в изучении чертежа и подумаем, как нам доказать требуемое. Какой признак может указывать на принадлежность точки О описанной окружности BCD?

Подсказка 3

Конечно, в нашем случае проще всего будет доказывать через равенство вписанных углов. Для каких двух углов будет удобнее это доказать?

Подсказка 4

Конечно, легче находится, что OBC и ODC равны и опираются на дугу ОС. Это несложно вывести, если увидеть равенство треугольников BKO и DCO. Теперь остаётся только последовательно всё доказать

Показать ответ и решение

Введём декартову систему координат с центром в точке $A$ , ось абсцисс — луч $AD$ , ось ординат — луч $AA ′$ , ось аппликат — луч $AB$ .

Пусть $′ O$ — проекция центра сферы на грань $′ ′ AA B B$ куба. Определим ее местоположение. Так как сфера касается прямых $′ ′′ AA ,A B$ и проходит через точку $B$ , то расстояние от точки $′ O$ до прямых $′ AA$ и $′ ′ A B$ и точки $B$ одинаково (обозначим его $r$ ). Тогда $′ O$ лежит на луче $′ A B$ , который является биссектрисой угла $′ ′ AA B$ . Осталось учесть условие, что центр сферы касается прямой $AD$ , то есть нужно проверить, что расстояние от центра до прямой $AD$ совпадает с радиусом сферы $OB$ .

Заметим, что есть два случая расположения точки $′ O$ (на рисунке показаны разными цветами):

$PIC$

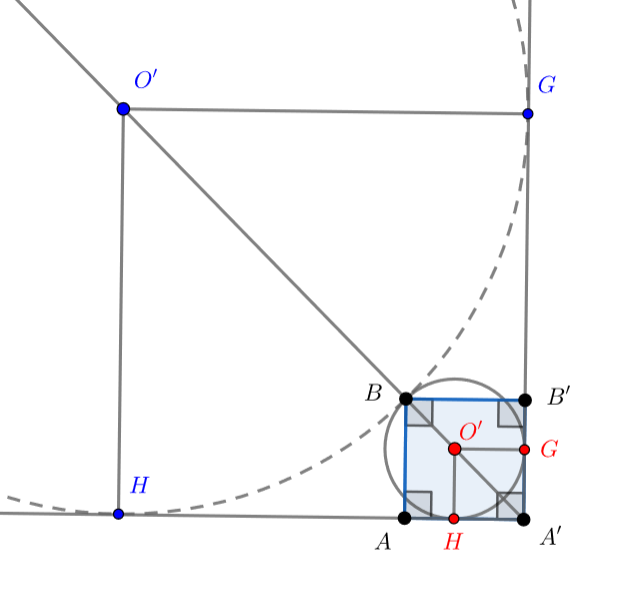
Случай 1: точка $O ′$ лежит на диагонали $A ′B$ .

Тогда из теоремы Пифагора для прямоугольного треугольника $O ′HA ′$ получим: $r2+ r2 = (√2-− r)2$ , откуда $r =2− √2$ . Значит, центр сферы $O$ имеет координаты $(x1;√2-− 1;2− √2)$ .

Расстояние до прямой $AD$ равно $∘(√2−-1)2-+(2−-√2)2$ . То есть радиус $OB = ∘(√2-− 1)2+(2−-√2)2 = ∘9−-6√2.$

Случай 2: точка $O ′$ лежит на продолжении луча $A′B$ .

Тогда из теоремы Пифагора для прямоугольного треугольника $O ′HA ′$ получим: $r2+ r2 = (√2-+r)2$ , откуда $r =2+ √2$ . Значит, центр сферы $O$ в этом случае имеет координаты $(x ;−√2-− 1;2+ √2) 2$ .

Расстояние до прямой $AD$ равно $∘--√-----2-----√--2 (− 2− 1) + (2+ 2)$ . То есть радиус $∘ --√----2-----√--2- ∘ ---√-- OB = (− 2− 1)+ (2+ 2) = 9+6 2.$

Ответ:

$∘9-±-6√2$

Ошибка.
Попробуйте повторить позже

Задача 3#83301

Точка $O$ — начало трех отрезков $OA,OB$ и $OC$ лежащих в плоскости $P$ и имеющих длины 3,4 и 7 соответственно. На прямой $L$ , проходящей через точку $O$ и перпендикулярной плоскости $P$ , расположена точка $D$ так, что сумма углов, образуемых прямыми $DA, DB$ и $DC$ с прямой $L$ , равна $∘ 180$ . Найти длину отрезка $OD$ .

Источники: Росатом-2024, московский вариант, 11.6 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Треугольники ODA, ODB и ODC прямоугольные, также они имеют общую сторону OD. Если её обозначить за переменную, как можно будет записать условие на сумму трёх углов?

Подсказка 2

Пусть OD = x, тогда углы выражаются через арктангенсы. Тогда из условия получаем, что сумма трёх арктангенсов равна π. Что же хочется сделать? Взять от обеих частей тангенс! Но для тангенса суммы двух углов мы формулу знаем, чего не скажешь о суммы трёх. А вот π одиноко стоит с правой стороны, тогда можно сначала перенести одно слагаемое на правую часть и потом уже делать махинации со взятием тангенса.

Подсказка 3

Тогда взяв тангенс от обеих частей (но помните, что нужно будет сделать проверку равносильности такого перехода!) и применив формулу тангенса суммы, получаем совсем простое квадратное уравнение для x.

Показать ответ и решение

Обозначим $OD$ через $x$ .

$PIC$

Из прямоугольных треугольников выражаем углы

∠CDO =arctg 7 ,∠BDO =arctg 4,∠ADO = arctg 3 x x x

По условию нам дано

arctg 7 +arctg 4 + arctg 3= π x x x

Преобразуем

7 4 3 arctgx +arctgx = π− arctg x

Возьмём тангенс от обеих частей (проверку равносильности такого перехода отложим) и применим формулу тангенса суммы

tg(arctg 7x)+ tg(arctg 4x) 3 1−-tg(arctg 7)⋅tg(arctg 4) = tg(π − arctgx) x x

-11x--= − 3 1− 28x2 x

28 11 1− x2 =− 3-

x2 = 28⋅3= 6 14

$x= OD >0,$ поэтому подходит только $x= √6$ .

Теперь вернёмся к уравнению до взятия тангенсов и подставим туда этот корень. Правая часть $∘ -- π− arctg 32$ лежит на отрезке $(0,π).$ Левая тоже, потому что оба арктангенса по определению положительные и меньше $π2.$ То есть они не могут отличаться на кратное $π.$ Так что раз тангенсы получились равны, то и сами углы равны.

Ответ:

$√6$

Ошибка.
Попробуйте повторить позже

Задача 4#83311

Медианы оснований треугольной призмы $ABCA B C 1 1 1$ пересекаются в точках $O$ и $O 1$ соответственно. На отрезке $OO 1$ взята точка $P$ так, что $O1P :PO = 3:5$ . Через точку $P$ проведена прямая параллельная диагонали $A1C$ боковой грани призмы. Найти длину отрезка этой прямой, расположенного внутри призмы, если длина диагонали $A1C$ равна 2.

Источники: Росатом - 2024, региональный вариант, 11.6 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Рассмотрим сечение призмы XYZT, проходящее через OO₁ и параллельное грани ACC₁A₁. Прямая, проходящая через точку Р и параллельная А₁С, будет лежать как раз в этом сечении. А искомый отрезок - это часть этой прямой, ограниченная четырехугольником XYZT. А какой фигурой является XYZT? Как относятся ее стороны к сторонам призмы?

Подсказка 2

Верно, XYZT - параллелограмм. ZT = XY = A₁A, XT = YZ = 2/3 * AC, так как точка пересечения медиан делит медианы в отношении 2 к 1. Теперь нужно подумать, с помощью чего мы можем "перенести" плоскость ACC₁A₁ на плоскость XYZT?

Подсказка 3

С помощью гомотетии! Сделаем гомотетию в точке В₁ с коэффициентом 2/3. Подумайте, куда перейдут точки, лежащие в плоскости ACC₁A₁.

Подсказка 4

Например, точка А₁ перейдет в точку Х. Постройте прямые, параллельные А1С, через точки Х и Z. Чему будут равны отрезки этих прямых, отграниченные параллелограммом XYZT? Равна ли искомая прямая этим отрезкам?

Показать ответ и решение

Рассмотрим сечение призмы $XY ZT$ , проходящее через $OO 1$ и параллельное грани $ACC A 1 1$ . Это параллелограмм, а $OO 1$ — его средняя линия.

Сделаем гомотетию в точке $B1$ с коэффициентом $2 3$ . Тогда точки $A1$ и $C1$ перейдут в $X$ и $T$ , потому что точка пересечения медиан делит медиану в отношении $2$ к $1$ . Точка $Q$ перейдёт в точку $Q1$ , делящую отрезок $OO1$ в отношении $2$ к $1$ (до гомотетии отрезок $P Q$ был половиной $PR$ , а после он перешёл в $XQ1$ , который равен $1 3PR$ ). При этом прямая $XQ1$ будет пересекать отрезок $TZ$ в точке $W$ , поскольку в параллелограмме $ACC1A1$ прямая $A1C$ пересекает вершину $C$ , а в параллелограмм $XYZT$ отличается от $ACC1A1$ лишь тем, что длины сторон $YZ$ и $XT$ короче, а значит, точка пересечения прямой $XQ1$ с прямой $TZ$ будет лежать ниже точки $Z$ .

$PIC$

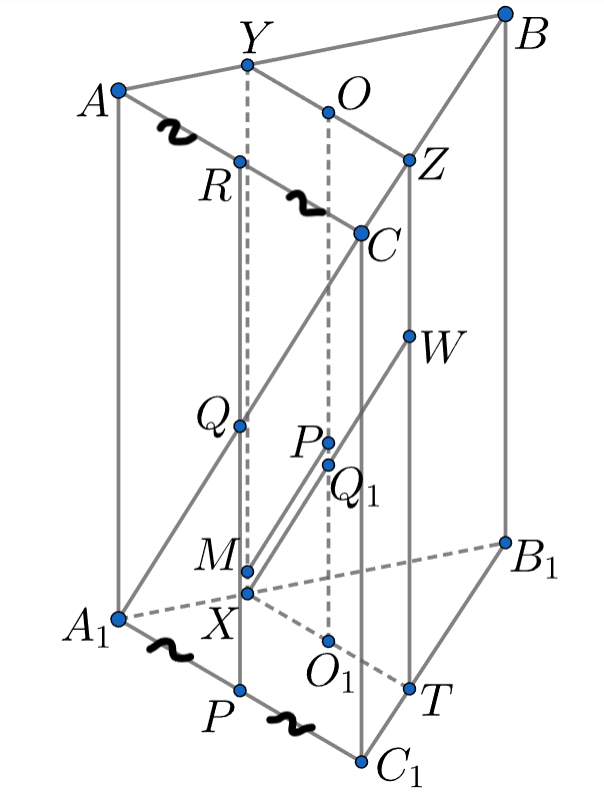
Аналогично, прямая, проходящая через $Z$ параллельно прямой $A1C$ будет делить $OO1$ в отношении $2$ к $1$ , но уже считая от точки $O$ , и она будет проходить через отрезок $XY$ . Значит, прямая $MP$ будет лежать между этими двумя прямыми и также проходить через отрезок $TZ$ . Значит, отрезок нужной прямой — это отрезок прямой $MP$ , содержащийся в параллелограмме $XY ZT$ .

Поскольку $MP ∥ XW$ , длина этого отрезка будет равна $XW$ . Отрезок $XQ1$ — образ $AQ$ при гомотетии, значит, он равен $23AQ = 23$ .

Также $XQ1 = Q1W$ , то есть искомая длина — $43$ .

Ответ:

$4 3$

Ошибка.
Попробуйте повторить позже

Задача 5#83740

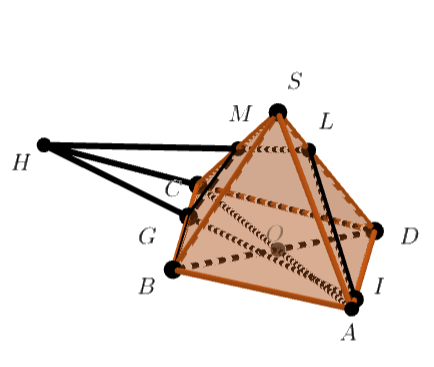
Параллелограмм $ABCD$ является основанием пирамиды $SABCD.$ Точки $M,N$ и $P$ лежат на рёбрах $SA,SD$ и $SC$ соответственно, причём

SM :MA = 1:2, SN :ND = 1:3, SP :PC =1 :4

В каком отношении плоскость $MNP$ делит ребро $SB?$

Источники: Звезда - 2024, 11.1 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

Построить точку пересечения плоскости MNP и ребра SB сразу так сложно. Кажется, не хватает какой-нибудь точки на MP, чтобы провести через неё и N прямую, пересекающую ребро SB в искомой точке (пусть K).

Подсказка 2

Да это же точка, получаемая пересечение MP и SO, где SO — пересечение плоскостей BSD и ASC, назовём её Т. Точку ввели, а как она делит SO — не узнали. А хотелось бы, потому что её можно рассмотреть и для △ASC (а мы знаем про то как делят его стороны M и P), и для △BSD (содержащий интересующую нас точку K).

Подсказка 3

Отношение ST : NO можно найти, рассмотрев △ASC. А ещё же у нас есть отношение AO : OC (подумайте, чем является точка O для основания). Часто, когда мы видим отношения отрезков, хочется применить теорему Фалеса, только вот нам не хватает несколько параллельных прямых... Какие можно провести, чтобы использовать оба упомянутых отношения на сторонах SA и AC?

Подсказка 4

В предыдущей подсказке попробуйте провести прямые из A и O параллельно MP. С помощью теоремы Фалеса можно найти отношение ST : NO. Если Вы всё правильно посчитали, то не составит труда, используя уже упомянутую теорему, найти отношение SK : KB.

Показать ответ и решение

Пусть плоскости $BSD$ и $ASC$ пересекаются по прямой $SO.$ Рассмотрим треугольник $ASC.$ Пусть $T = MP ∩ SO.$

$PIC$

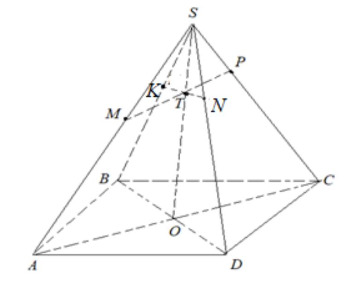
В треугольнике $ASC$ проведём прямые $AL$ и $OQ$ параллельные $MP.$

$PIC$

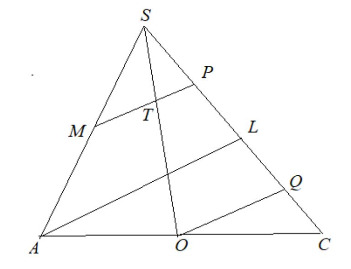
По теореме Фалеса имеем

SPPL-= SMMA- = 12, LQQC-= AOOC- =1

Учитывая, что $SP :PC =1 :4,$ получаем, что

ST-= 1 TO 3

Пусть $K = NT ∩ SB.$ Так как

SN :ND = ST :TO =1 :3,

то в силу теоремы Фалеса прямые $BD$ и $NK$ параллельны, и, следовательно,

SK :KB =1 :3

Ответ: 1:3

Ошибка.
Попробуйте повторить позже

Задача 6#85564

В пирамиде $SABCD$ с вершиной $S$ известно, что $AB = 9,BC =$ 5 и $CD = 13$ . Найдите длину ребра $AD$ , если вписанная в пирамиду сфера касается основания в точке пересечения диагоналей четырёхугольника $ABCD$ .

Источники: Курчатов - 2024, 11.5 (см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Сфера даёт очень много точек касания, а значит, очень много равных отрезков касательных. Попробуйте найти пары равных треугольников (их точно больше 5).

Подсказка 2

Вы получили очень много равных углов, но отдельных равенств недостаточно, тогда как бы их объединить? Вспомните, чему равна сумма углов вокруг точки, и посчитайте такие суммы для точек касания сферы боковых сторон.

Подсказка 3

Из полученных равенств попробуйте найти угол между диагоналями основания. Это знание и поможет посчитать искомую сторону:)

Показать ответ и решение

Обозначим точки касания сферы с гранью основания и гранями $SAB, SBC,SCD$ и $SDA$ буквами $H,K ,K ,K 1 2 3$ и $K 4$ соответственно.

По свойству отрезков касательных, соответствующие отрезки касательных к сфере будут равны. Значит, по признаку равенства по трём сторонам будут равны треугольники

△K1AB = △HAB, △K2BC = △HBC, △K3CD = △HCD, △K4DA = △HDA,

а также

△K1SB =△K2SB, △K SC =△K SC, 2 3 △K3SD =△K4SD, △K4SA = △K1SA.

Следовательно, будут равны все соответствующие углы этих треугольников.

$PIC$

Поскольку вертикальные углы между диагоналями $ABCD$ равны, то будут равны углы $∠AK1B = ∠CK3D$ и $∠BK2C = ∠DK4A$ .

Рассматривая суммы углов $360∘$ вокруг точек $K1,K2,K3$ и $K4$ получаем, что все углы равны:

∠AK1B =∠BK2C =∠CK3D =∠DK4A.

Так как эти же углы получаются между диагоналями в основании $ABCD$ и образуют вокруг точки $H$ в сумме $360∘$ , то углы прямые и диагонали $AC$ и $BD$ перпендикулярны.

Обозначим длины отрезков $AH,BH,CH$ и $DH$ за $a,b,c$ и $d$ соответственно. Применяя теорему Пифагора для треугольников $ABH, BHC$ и $CHD$ получим равенства:

2 2 2 a + b = 9, b2+ c2 = 52, c2+ d2 = 132.

Складывая первое и третье и вычитая второе равенство, получим $d2+ a2 =$ $132+92− 52 = 152$ . Из теоремы Пифагора для треугольника $DAH$ находим отрезок $AD = 15$ .

Ответ: 15

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#86474

Основанием четырехугольной пирамиды $SABCD$ является параллелограмм $ABCD$ со сторонами $AB =2√3,AD = 4√3$ и углом $A$ , равным $∘ 60$ . Высотой пирамиды $SABCD$ является отрезок $SO$ , где $O$ - точка пересечения диагоналей параллелограмма $ABCD, SO = 1$ . Найдите площадь сечения пирамиды $SABCD$ плоскостью, параллельной медиане $SE$ боковой грани $SAB$ и проходящей через середину ребра $SC$ и середину отрезка $AO$ .

Источники: ШВБ - 2024, 11.5 (см. olymp.bmstu.ru)

Подсказки к задаче

Подсказка 1

То, что в условии нам даны все длины, может подтолкнуть к тому, что это очень техническая задача. Здесь придется много считать и не бояться больших и страшных дробей. Первым делом нужно построить сечение. Поищите точку, принадлежащую сечению, на плоскости ABCD.

Подсказка 2

Теперь рассмотрим саму плоскость ABCD. У нас есть прямая, лежащая в этой плоскости и принадлежащая сечению. Где эта прямая пересекает прямые, содержащие стороны параллелограмма ABCD? Найдите отношения с помощью теоремы Менелая и подобия.

Подсказка 3

Пусть эта прямая пересекает прямые AB,BC,CD, AD в точках F,G,H,I соответственно. Пусть L - точка, в которой прямая HM пересекает ребро SD. Тогда искомое сечение это LMGI. Найдем его площадь как разность площадей треугольников LHI и MGH. А как найти их площади? Много считать длины сторон и отношения, используя теоремы Менелая, Герона, Пифагора, косинусов.

Показать ответ и решение

Пусть $M$ — середина ребра $SC,$ а точка $K$ - середина отрезка $AO$ . Рассмотрим плоскость $(CSE)$ . Так как плоскость сечения параллельна медиане $SE$ и проходит через точку $M$ , построим прямую $MT ||SE$ в плоскости $(CSE )$ . Тогда $MT$ - средняя линия в $CSE$ , а $T$ середина $CE$ .

Теперь нам известны три точки сечения: $T,M, K$ . Рассмотрим основание пирамиды $ABCD$ и посмотрим, как прямая $TK$ пересекает стороны основания. Пусть эта прямая пересекает прямые $AB,BC,CD, AD$ в точках $F,G,H,I$ .

$PIC$

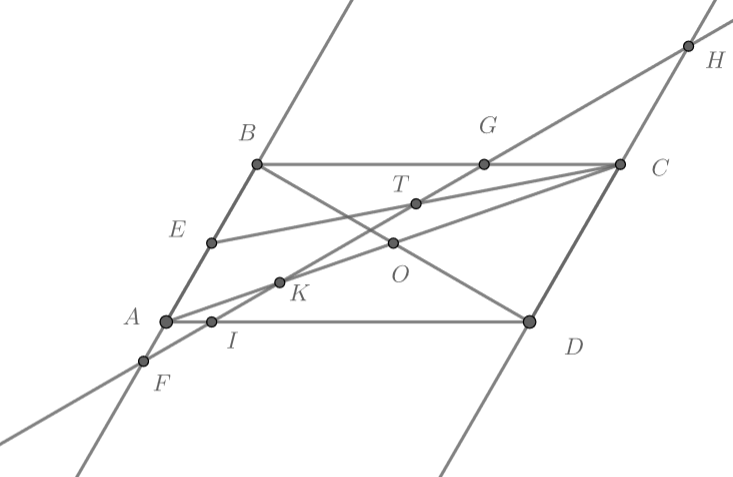
Из теоремы Менелая для треугольника $ACE$ получаем, что

EF-= CK-⋅ TE-= 3 FA AK CT 1

Так как $EA = 1AB 2$ , то $FA = 1AB 4$ .

Далее замечаем, что $△F AK ∼ △HCK$ . Тогда

AF- AK- 1 HC = CK = 3

Откуда $3 HC =3AF = 4AB$ .

Из подобия $△FAI ∼△HDI$ получаем

AI AF 1 ID-= DH-= 7

То есть $AI = 18AD$ .

Аналогично из подобия $△FBG ∼ △HCG$ получаем

BG-= FB-= 5 GC CH 3

То есть $BG = 58BC$ .

Проведем $GG ′||CD$ , где $G′$ - точка на $AD$ . Тогда

GG ′ =AD = 2√3;G′I =AD − 3BC − 1BC = BC-= 2√3 8 8 2

И $∠GG ′I =180∘− ∠A= 120∘$ . Тогда из теоремы косинусов для треугольника $GG ′I$ получим $IG = 6$ .

$PIC$

Пусть $L$ - точка, в которой прямая $HM$ пересекает ребро $SD$ . Тогда из теоремы Менелая для $△CSD$ и прямой $HM$ получим:

7 DL-= CM- ⋅ DH =1⋅-4CD = 7 SL SM CH 34CD 3

Далее из теоремы Менелая для $△DHL$ имеем:

HM CH SD 5 ML--= DC-⋅-SL = 2.

В силу параллельности прямых $BC$ и $AD$ имеем $HHGI-= 37$ , откуда $HG = 92,HI = 212$ . По теореме косинусов для $△ABD$ имеем $BD = 6$ , то есть $OD = 3$ . Из теоремы Пифагора для треугольника $SOD$ получаем $SD =√10-$ , откуда $7√10 DL = 10$ . По теореме косинусов для $△ADC$ имеем $√-- 2 21$ , а значит $√ -- TC = 21$ . По теореме Пифагора для $△SOC$ вычислим $√-- SC = 22$ . Заметим, что для треугольника $SDC$ выполняется теорема Пифагора, то есть угол $SDC$ прямой. С помощью теоремы косинусов для треугольника $SAD$ вычислим $3√30 cosSDA = 20$ . Теперь через теоремы косинусов для треугольников $LDI$ и $LDH$ вычислим длины отрезков $7√10- 7√85- IL = 5 ,LH = 10$ . Далее по теореме Герона получаем $147- S△ILH = 20$ .

Заметим, что $1 1 5 3 15 S△MHG = 2sin∠MHG ⋅MH ⋅GH = 2sin∠MHG ⋅7HL⋅ 7HI = 49S△HLI$ . Значит, $34 34 147 51 SLMGI = S△LHI − S△MHG = 49S△LHI = 49-⋅20 = 10$ .

Ответ: 5.1

Ошибка.
Попробуйте повторить позже

Задача 8#91958

Плоскость $π$ перпендикулярна ребру $SA$ правильной треугольной пирамиды $ABCS$ с вершиной $S$ и основанием $ABC$ , делит это ребро в отношении $1:2$ (считая от вершины $S$ ) и проходит через середину ребра $SB$ . Найдите угол между плоскостью $π$ и плоскостью основания пирамиды.

Источники: ДВИ - 2024, вариант 241, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте построим сечение MNK (M∈AS, N∈SB, K∈SC) пирамиды SABC плоскостью π. Обозначим AS = 6х и попробуем выразить все отрезки на рисунке через х (для этого можно воспользоваться теоремой косинусов для треугольника △ASB, ведь cos∠ASB мы можем без проблем найти, так как на рисунке есть очень много прямоугольных треугольников)

Подсказка 2

Проведём LN — среднюю линию треугольника △ASB, обозначим за Р середину NK. Какой угол требуется найти в задаче?

Подсказка 3

Конечно, угол ∠MPL! Так как мы уже знаем соотношение практически всех отрезков, мы можем без труда найти значение синуса этого угла)

Показать ответ и решение

Первое решение.

Пусть $π$ пересекает $AS,$ $BS$ и $CS$ в точках $P,$ $R$ и $Q$ соответственно (то есть $π = (PQR )).$ Тогда по условию $SR = RB$ и $AP = 2PS.$ Пусть $M$ — середина $BC.$ Тогда пирамида $SABC$ симметрична относительно плоскости $(SAM ).$ Поскольку $π$ пересекает ребро $SB$ в середине, то в силу симметрии эта плоскость пересекает $CS$ тоже в середине, поэтому $QC = QS.$

$PIC$

Пусть $K$ — середина $AP.$ Тогда $PS =P K = AK,$ так как $AP = 2P S.$ Тогда, поскольку $SP :PK = SR :RB,$ то $PR$ и $KB$ параллельны. Аналогично можно доказать, что $RQ$ и $BC$ параллельны. Таким образом, $π$ и $(KBC )$ — параллельные плоскости, поэтому требуемый в задаче угол равен углу между $(KBC )$ и $(ABC ).$

Так как по условию $π$ и $AS$ перпендикулярны, то $(KBC )$ и $AS$ перпендикулярны, то есть $BK$ и $CK$ перпендикулярны $AS.$ Снова применив соображение симметрии, получаем, что $KB = KC,$ то есть $△KBC$ — равнобедренный, и $KM$ — его высота, поскольку $M$ является серединой $BC.$ Так как $ABC$ — правильный треугольник (по условию $SABC$ — правильная пирамида), то $AM$ — тоже высота в треугольнике $ABC.$ Таким образом, $KM$ лежит в плоскости $(KBC )$ и перпендикулярно $BC,$ а $AM$ лежит в плоскости $ABC$ и перпендикулярно $BC.$ Эти плоскости пересекаются по прямой $BC.$ Таким образом, нужный угол по определению равен $∠KMA.$

Пусть $AB = BC = AC = 2a.$ Тогда $BM =MC =a,$ так как $M$ — середина $BC.$ По теореме Пифагора из треугольника $ABM$ получаем $AM = √3a.$ По теореме Пифагора из треугольника $KSB$ получаем $KB2 = 5x2.$ С другой стороны, по теореме Пифагора из треугольника $AKB$ имеем $KB2 = 4a2− x2.$ Таким образом, $4a2 − x2 = 5x2,$ то есть $∘ -- x = 23a.$

Так как $KBC$ и $AS$ перпендикулярны, то $KM$ и $AS$ перпендикулярны. Из прямоугольного треугольника $AKM :$

∘ -- x 2a √2- sin ∠AMK = √3a-= √33a-= -3-

Таким образом, $√- ∠AMK = arcsin-23 .$

______________________________________________________________________________________________________________________________________________________

Второе решение.

Пусть $π$ пересекает $AS$ в точке $H,$ $BS$ — в точке $M.$ Пусть $AS = CS =BS = 6x.$ Тогда из условия следует, что $SH =2x,$ $AH = 4x,$ так как $SH :AH = 1:2.$ $M$ — середина $SB,$ поэтому $SM = SB =3x.$

$PIC$

По теореме Менелая для треугольника $ASC$ и прямой $HT :$

4x 3x CT- 2x ⋅3x ⋅TA = 1

Таким образом, $TA =2CT,$ поэтому $AC = CT.$ Пусть $AC = y.$ По теореме Менелая для треугольника $AHT$ и прямой $SC :$

y TM 2x y ⋅MH--⋅6x = 1

Таким образом, $TM = 3MH.$ Так как $AS$ по условию является перпендикуляром к плоскости $π,$ то $T H$ и $AS$ перпендикулярны. Тогда по теореме Пифагора из треугольника $SMH$ получаем $√- HM = 5x.$ То есть $√- TM = 3 5x.$ По теореме Пифагора для треугольника $AHT :$

16x2 +80x2 = 4y2

Таким образом, $√- y = 2 6x.$ Пусть $O$ — основание высоты пирамиды $SABC.$ Углы между плоскостями равны углам между перпендикулярами к ним, поэтому

∠(π,(ABC )) =∠(SA,OS)

Из прямоугольного треугольника $ASO$ получаем $sin∠ASO = AAOS-.$ Так как $O$ — точка пересечения медиан правильного треугольника $ABC,$ то $√- √- AO = -33 y = 2 2x.$ Тогда

√- √- sin∠ASO = AO-= 2-2x = -2- AS 6x 3

Таким образом, $∠ASO = arcsin√2. 3$

______________________________________________________________________________________________________________________________________________________

Третье решение.

Пусть искомый угол это $φ.$ Обозначим пересечение плоскости $π$ с ребрами $SA, SB, SC$ точками $M, N, K$ соответственно. $N$ — середина ребра $SB,$ следовательно, $K$ тоже середина ребра, так как пирамида правильная. По условию $NM ⊥ SA, KM ⊥ SA.$ Обозначим длину $SA$ как $6x,$ тогда получаем, что

SM = 2x, AM = 4x, SN = NB = SK =KC =3x

$PIC$

В треугольнике $MSN :$

2x 2 cos∠MSN = 3x = 3

Тогда по теореме косинусов для треугольника $ASB$ получаем

2 2 2 2 2 2 2 AB = AS + SB − 2⋅AS⋅SB ⋅cos∠MSN = (6x) +(6x) − 2⋅6x⋅6x⋅3 =24x

√- AB = 2x 6

Обозначим середину ребра $SA$ точкой $L.$ Тогда треугольник $LNK$ правильный, так как треугольник $ABC$ правильный, а также плоскость $(LNK )$ параллельна плоскости основания. $LN$ — средняя линия в треугольнике $ASB,$ следовательно, $LN =x√6.$ Обозначим точкой $P$ середину $NK.$ В треугольнике $LNK :$

LN √3 3x√2- LP = --2-- =--2-

так как треугольник $LNK$ правильный.

Так как плоскость $(LNK )$ параллельна плоскости основания, то найдем угол между этой плоскости и плоскости $π.$

MP ⊥ NK, LP ⊥ NK =⇒ ∠LPM = φ

Так как $L$ — середина, то $LM =x.$ В прямоугольном треугольнике $LP M (MP ⊥SA )$ находим, что

LM x √2 sin∠LPM = -LP = 3x√2-= -3- 2

Тогда

√- ∠LMP = φ =arcsin -2- 3

Ответ:

$arcsin√2 3$

Ошибка.
Попробуйте повторить позже

Задача 9#96230

Найдите синус угла между высотами, опущенными из двух вершин правильного тетраэдра на противоположные грани.

Показать ответ и решение

Пусть дан правильный тетраэдр $SABC$ со стороной $a,$ в котором проведены высоты $SS′$ и $AA ′,$ пересекающиеся в точки $H.$ Отметим середину $BC$ как $K$ и проведём медианы $AK$ и $SK$

$PIC$

В силу того, что тетраэдр правильный, точки $′ A$ и $′ S$ будут является центрами соответствующих граней, а значит будут лежать на $SK$ и $AK$ соответственно. Заметим, что четырёхугольник $′ ′ HA KS$ вписанный по двух двух прямым противолежащим углам, следовательно, $′ ′ ∘ ′ ′ ∠A HS =180 − ∠AKS ,$ поэтому $′ ′ ′ ′ sin ∠AHS = sin∠A KS .$ Так как $AK$ и $SK$ — медианы в правильных треугольниках, они равны $√ - --3a. 2$ Сделаем выносной чертёж треугольника $ASK,$ проведя его медиану $KM$

$PIC$

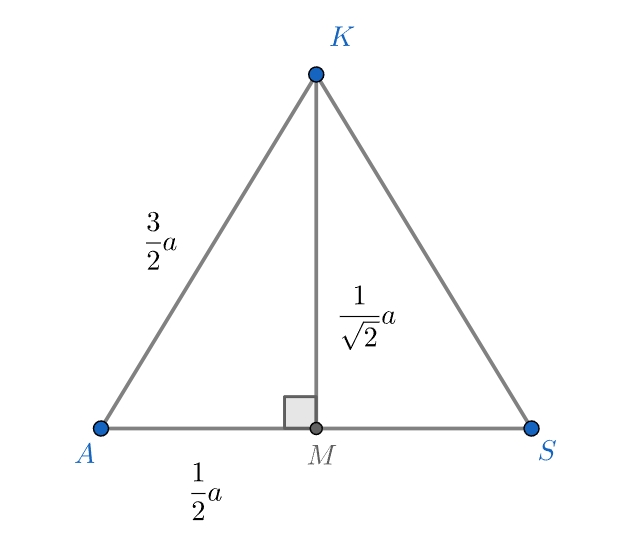
Так как треугольник $ASK$ равнобедренный, то $KM$ является биссектрисой и высотой, поэтому

1a sin∠AKS- =sin ∠AKM = AM- = √2--= √1- 2 AK --3a 3 2

По теореме Пифагора $KM = √1a, 2$ поэтому

√1-a √ - cos∠AKS-= cos∠AKM = KM-= √-2-= √-2 2 AK --3a 3 2

В итоге получаем, что

∠AKS ∠AKS 1 √2 2√2 sin∠AKS = 2sin--2-- cos--2-- = 2√3√3-= -3-

Ответ:

$2√2 3$

Ошибка.
Попробуйте повторить позже

Задача 10#99239

Для монтажа бурового оборудования в скважину используется подвес, состоящий из металлического каркаса в форме равностороннего треугольника и трёх регулируемых по длине тросов протянутых через вершины треугольника и соединяющихся на крюке. Расстояние между тросами на каркасе составляет $2$ м, а их первоначальная длина от каркаса до крюка — $3$ м. При спуске оборудования оказалось, что крюк нужно сместить на $√3 12$ м вдоль медианы каркаса по направлению от вершины. На сколько метров нужно удлинить трос, проходящий через эту вершину?

Источники: Газпром - 2024, 11.6 (см. olympiad.gazprom.ru)

Подсказки к задаче

Подсказка 1

Из условия следует, что у нас изначально есть правильный тетраэдр со стороной 2. После этого мы как-то меняем положение крюка, чтобы точка вершины сдвинулась вдоль медианы в основании на нужную длину. Подумайте, что это значит в терминах геометрии.

Подсказка 2

Это значит, что проекция вершины S на плоскость основания сместилась на нужную длину, но при этом проекция S всё равно лежит на медиане. Если S₁ — новая точка, то мы можем посчитать S₁O₁ как катет прямоугольного треугольника S₁DO₁, где D — середина BC, а O₁ — сдвинутая на нужную длину точка O. Но тогда мы можем найти и S₁A (из какого прямоугольного треугольника?), а значит, и разность длин троса. Ну и всё, идейно задача решена, осталось посчитать!

Показать ответ и решение

Пирамида $SABC$ — правильная, тогда медиана

√3 √ - AD = AB ⋅sin60∘ =2 ⋅2-= 3,

а апофема

∘ --------- ∘------ √- SD = SB2 − BD2 = 32− 12 = 2 2.

Так как $O$ — точка пересечения медиан треугольника $ABC$ , то

√- √- AO = 2AD = 2-3, DO = 1AD = -3. 3 3 3 3

При увеличении длины троса $SA$ проекция вершины пирамиды переместиться в точку $O1$ , так что $√- OO1 = 132$ , тогда

√ - √- √ - √- √- √ - AO1 = 2-3+ -3-= 3-3, DO1 = -3-− -3= --3. 3 12 4 3 12 4

Поскольку, при увеличении длины троса $SA$ до $SA 1$ длина апофемы треугольника $S BC 1$ равна $S D= SD 1$ , то

┌ ------------- ∘ --------2- ││∘ √ - ( √3)2 ∘ 125 5√5 S1O1 = S1D2− DO1 = (2 2)2− 4-- = 16-= -4-.

Следовательно,

┌ ---------------- ∘---------- ││ ( 5√5-)2 (3√3-)2 ∘-152 ∘ --- S1A = S1O21 + AO21 =∘ -4- + -4- = 16-= 9,5.

Тогда трос нужно удлинить на $√9,5− 3$ .

Ответ:

$√9,5− 3$

Ошибка.
Попробуйте повторить позже

Задача 11#68657

В правильной треугольной пирамиде дана сторона основания $a$ и высота $h$ . Найти длину бокового ребра.

Подсказки к задаче

Подсказка 1

По условию нам дана длина высоты и сказано, что пирамида правильная. Давайте проведем эту высоту, тогда в какую точку на основании пирамиды она упадет?

Подсказка 2

Если опустить высоту в правильной пирамиде, то основание высоты совпадёт с центром основания пирамиды.

Подсказка 3

По условию нам дана длина стороны основания, значит, мы можем найти радиус описанной окружности около основания, следовательно, можем найти боковую сторону пирамиды по теореме Пифагора.

Показать ответ и решение

$PIC$

Пусть это пирамида $SABC$ , $O$ — центр основание. Поскольку основание является правильным треугольником, то $AO= AB√3 = √a3$ , а также $AO ⊥ OS$ , отсюда легко найти $∘ ------ AS = √AO2-+-SO2 = a2+ h2 3$ .

Ответ:

$∘ a2+-h2 3$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#68659

Одна из высот некоторого тетраэдра проходит через точку пересечения высот противоположной грани. Докажите, что все остальные высоты тетраэдра обладают этим же свойством.

Подсказки к задаче

Подсказка 1

Нам нужно получить, что все высоты обладают этим свойством. Может, надо найти какие-то связи между ребрами тетраэдра...

Подсказка 2

Пускай для определенности именно высота DH обладает этим свойством. Тогда H- ортоцентр треугольника ABC. На картинке много прямых углов, пора использовать теорему о трех перпендикулярах!

Подсказка 3

Но применять ее нужно хитро: попробуйте провести через точку A прямую, параллельную BC, и использовать нашу любимую теорему!

Подсказка 4

Получается, что AD перпендикулярна прямой, параллельной BC. Но тогда AD перпендикулярна BC. Это мы выяснили, поработав только с точкой A. Может, нужно поработать с точками B и C...

Подсказка 5

Аналогично рассуждая, можно прийти к тому, что BD перпендикулярна AC и CD перпендикулярна AB. Получается, что скрещивающиеся ребра попарно перпендикулярны. Попробуйте теперь провести высоту AN и доказать, что N- ортоцентр BCD.

Подсказка 6

Достаточно доказать, что BN- отрезок высоты треугольника BCD. Попробуйте провести похожие рассуждения с 3 подсказкой, только с обратной теоремой о трех перпендикулярах, и будет вам счастье!

Показать доказательство

$PIC$

Пусть это тетраэдр $ABCD$ и $DD0 ⊥ AD0$ — данная в условии высота, откуда $AD0 ⊥ BC$ .

Проведём $AA1 ∥BC =⇒ AD0 ⊥ AA1$ . Используя теорему о трёх перпендикулярах для $DD0,AD0, AA1$ , имеем $AD ⊥ AA1 =⇒ AD ⊥ BC$ . Аналогично в силу симметрии можно заключить $AB ⊥CD, AC ⊥BD$ . Мы доказали попарную перпендикулярность противоположных рёбер тетраэдра.

Рассмотрим теперь высоту $CC0$ и проведём $DD1 ∥AB.$ Поскольку $AB ⊥ CD,DD1 ⊥ CD$ , то по обратной теореме о трёх перпендикулярах $DD1 ⊥C0D$ или $AB ⊥ C0D$ . Значит, $C0$ лежит на высоте грани из вершины $D$ . Аналогично показываем, что она лежит и на других высотах, откуда и получаем требуемое.

Ошибка.
Попробуйте повторить позже

Задача 13#68660

Объём правильной треугольной пирамиды равен одной шестой куба бокового ребра. Найдите плоский угол при вершине.

Подсказки к задаче

Подсказка 1

Наверное, вся сложность этой задачи состоит в том, как искать плоский угол. Может попробовать найти его половинку, ведь для этого всего-то надо найти отношение бокового ребра к ребру основания...

Подсказка 2

Пускай ребро основания равно a, боковое ребро- x. Попробуйте расписать объём пирамиды через a и x, тогда мы найдем связь между ними (не забудьте, что по условию объем также равен x³/6)

Подсказка 3

Приравняв объем, выраженный через a и x, к x³/6, можно поделить обе части на a³ и сделать замену t=x/a. Осталось только решить иррациональное уравнение...

Подсказка 4

Можно возвести обе части в квадрат и сделать замену s=t². Подберите корень в кубическом уравнении (подставьте например 1 или -1...) и доведите решение до конца!

Показать ответ и решение

Первое решение.

$PIC$

2 V = 1 a3 = 1a-sin(α)h 6 3 2

1a3 = 1a2sin(α)h 6 6

Так как

1 1 2 SCDB = 2a ⋅h = 2a ⋅sin(α),

то

({a⋅h =a2⋅sin(α) ( a= sin(α)h

Решая данную систему, получаем:

2 sin(α)= 1

∘ α= 90

________________________________________________________________________________________

Второе решение. Пусть ребро основания равно $AB = a$ , а боковое — $AS = x$ .

$PIC$

Тогда объём пирамиды можно посчитать по формуле (высоту легко найти из теоремы Пифагора)

√ - ∘ ------ V = 1⋅--3a2 x2− a2= 1x3 3 4 3 6

Мы составили уравнение, остаётся понять, что искать. Оказывается, нам достаточно найти $sin∠ASH = AH-= -a AS 2x$ , проще говоря, достаточно найти значение $a x$ . Зная это, преобразуем уравнение, сделав замену $x t= a$ (для этого поделим обе части на $3 a$ )

√ -∘----- --3 t2− 1= t3 ⇐⇒ 3(t2− 1∕3)= t6 ⇐⇒ t6− 3t2+ 1= 0 2 3 4 4 4

После замены $t2 = s$ получаем

3 3 1 s −4s+ 4 = 0

Сразу несложно увидеть решение $s= −1.$ Вынося его, получим

2 (s+ 1)(s − s+ 1∕4)= 0 ⇐⇒

Получаем $s =− 1$ или $s= 1, 2$ откуда $t= ±√1. 2$ Подойдёт только $x= √1 a 2$ , откуда $sin ∠ASH = a-= 1√-= sin45∘ 2x 2$ , значит, $∠ASB = 90∘$ .

Ответ:

$90∘$

Ошибка.
Попробуйте повторить позже

Задача 14#69437

В параллелепипеде $ABCDA B C D 1 1 1 1$ точка $T−$ середина ребра $BB ,P 1$ лежит на ребре $AD$ так, что $AP :PD = 1:4.$

(a) Постройте сечение параллелепипеда плоскостью $C1TP.$

(b) Найдите отношение, в котором секущая плоскость делит ребро $DD1.$

Подсказки к задаче

Подсказка 1

Для того, чтобы построить сечение, нужно пересечь наш параллелепипед плоскостью. Давайте вспомним, что плоскость пересекает другую плоскость по прямой. А прямая строится по двум точкам. Как мы это можем использовать?

Подсказка 2

Давайте попробуем пересечь нашей плоскостью грань C₁B₁BC. Наша плоскость и данная грань пересекаются по прямой, а еще мы уже знаем две точки - C₁ и T, лежащие в пересечении. Значит, наша плоскость пересекает эту грань по какой прямой?

Подсказка 3

Верно, по прямой через точки C₁ и T! Проведем ее до пересечения с ребром CB (точка L) и попробуем найти пересечение нашей плоскости со следующей гранью - ABCD. Мы снова уже знаем две точки, которые точно лежат в пересечении - L и P! Значит, можно проделать тот же самый трюк. Осталось доделать сечение теми же методами!

Подсказка 4

Для того, чтобы найти отношение, было бы здорово использовать утверждения о том, как точки T и P делят стороны, а еще - найти подобных треугольников, чтобы эти знания использовать.

Подсказка 5

Например, треугольники LBT и LCC₁ - подобны, и мы даже знаем, с каким коэффициентом (вспомните, как точка T делит отрезок BB₁). Для удобства можно за х обозначить BB₁, и за y обозначить DA. После этого мы можем рассмотреть подобие треугольников MPA и MBL. И у нас еще есть подобие ODP, PAM. Пользуясь ими тремя и аккуратным счетом, можно достигнуть успеха!

Показать ответ и решение

(a) Проведем прямую $C T 1$ , пусть она пересечет $CB$ в точке $L$ . Далее проведем прямую $LP$ , пусть она пересечет $BA$ в точке $M$ и прямую $CD$ в точке $O$ . Затем проведем отрезок $OC1$ , пусть он пересечет $DD1$ в точке $N$ . Плоскость $C1TMP N$ и будет искомым сечением

$PIC$

(b) Пусть отрезки $B1T$ и $TB$ равны $y$ , а отрезок $CB =x$ . Тогда $CC1 = 2y$ . Заметим, что

△CC1L ∼ △BT L =⇒ C1C-= CL- =⇒ T B BL

=⇒ x-+BL-= 2 =⇒ BL= x BL

Так как $DP- 4x x P A =4 =⇒ DP = 5 , PA = 5.$

Пусть $AM = z$ . Заметим, что

BL MB △PAM ∼△MBL =⇒ PA-= AM--=5 =⇒

=⇒ MB = 5AM =5z =⇒ AB =DC =6z

Заметим, что $DP- OD- △ODP ∼△P AM =⇒ PA = AM = 4 =⇒ OD = 4AM = 4z$ .

Далее воспользуемся тем, что $△ODN ∼ △OCC1$

OD ND 4 ND 4y OC- =CC1- =⇒ 10 =-2y- =⇒ ND = -5

Тогда

D1N =2y− 4y= 6y =⇒ D1N-= 3 5 5 ND 2

Ответ: 3:2

Ошибка.
Попробуйте повторить позже

Задача 15#69820

В треугольной пирамиде $ABCD$ на ребре $AB$ взята точка $P$ так, что $AP :P B =$ $1 :2,$ на ребре $AD$ взята точка $Q$ так, что $AQ :QD = 2:3$ и на ребре $BC$ точка $R$ такая, что $BR :RC =3 :1.$ В каком отношении отрезок $QR$ делится плоскостью $CDP ?$

Источники: САММАТ-2023, 11.1 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

У нас в задачке даны отношения отрезков. В лоб как-то считать не очень хочется... Может, применить метод масс?

Подсказка 2

Мы хотим понять, в каком отношении плоскость CDP делит QR. Если мы добьемся того, чтобы центр масс G тетраэдра лежал одновременно в плоскости CDP и на отрезке QR, то QG/GR- и будет искомым отношением. Теперь надо расставить массы, чтобы эти условия выполнялись...

Подсказка 3

Чтобы G лежал в плоскости CDP достаточно, чтобы центр масс концов отрезка AB совпадал с P. Тогда: m(A)/m(B)=PB/PA=2. А как сделать так, чтобы G лежал на отрезке QR?

Подсказка 4

Достаточно, чтобы центр масс концов отрезка CB попадал в R, а отрезка AD- в Q. Тогда: m(C)/m(B)=BR/CR=3 и m(A)/m(D)=DQ/AQ=3/2. Какие массы надо взять, чтобы выполнялись все отношения?

Подсказка 5

Можно, например, взять m(A)=6, m(B)=3, m(C)=9 и m(D)=4. Тогда после группировки в Q будет масса 10, а в R- 12. Посчитайте отношение QG/GR и радуйтесь!

Показать ответ и решение

$PIC$

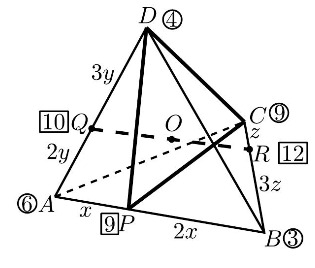
Применим метод масс. Поместим в вершины пирамиды такие массы: $A − 6,B − 3,C − 9,D− 4.$

Если из точек $A$ и $B$ убрать обе массы и поставить их сумму в точку $P,$ то центр тяжести всей системы не изменится, поэтому он будет лежать в плоскости $CDP.$

С другой стороны, если убрать две массы из точек $A$ и $D$ и вместо них поставить суммарную массу $6+4 =10$ в точку $Q,$ а вместо точек $B$ и $C$ поставить суммарную массу $3+9 =12$ в точку $R,$ то центр тяжести также не изменится и значит он будет находиться на отрезке $QR.$

Таким образом, центр тяжести данной системы будет расположен в точке пересечения прямой $QR$ и плоскости $CDP,$ то есть в точке $O.$

Значит, $QO :OR =12:10= 6:5.$

Ответ:

$6 :5$

Ошибка.
Попробуйте повторить позже

Задача 16#37309

Основанием прямой треугольной призмы $ABCA B C 1 11$ является прямоугольный треугольник $ABC$ , причем $∠C = 90∘$ . Диагонали боковых граней $AA1B1B$ и $BB1C1C$ равны соответственно $26$ и $10,AB = 25.$

(a) Докажите, что $△BA1C1$ прямоугольный.

(b) Найдите объем пирамиды $AA1C1B$ .

Подсказки к задаче

Подсказка 1

Часто, чтобы доказать в стереометрии, что какие-то две прямые перпендикулярны, нужно найти такую плоскость, для которой одна из прямых содержится в этой плоскости, а другая перпендикулярна этой плоскости. Попробуйте сделать то же самое в этой задаче для прямых A₁C₁ и C₁B.

Подсказка 2

Да, во-первых, A₁C₁ перпендикулярна C₁B₁, так как треугольник A₁B₁C₁-прямоугольный, а во-вторых, A₁C₁ перпендикулярна C₁C, в силу того, что перед нами призма. Значит, A₁C₁ перпендикулярна всей плоскости C₁CB. Значит, и прямой C₁B. Также, мы знаем два отрезка в треугольнике A₁C₁B , и знаем, что он прямоугольный. Кажется, теперь задача превратилась в счетную, где можно найти все отрезки(ведь тут одни прямоугольные треугольники). Осталось посчитать!

Показать ответ и решение

$PIC$

Поскольку $A1C1 ⊥ CBB1C1$ ( $A1C1 ⊥ CC1$ и $A1C1 ⊥ C1B1$ ), то, в частности, $A1C1 ⊥ BC1$ . По теореме Пифагора для $△BA1C1$ имеем $A1C1 =24$ . А по той же теореме для $△A1B1C1$ получим $B1C1 =7$ и для $△BAA1$ $√ -- AA1 = 51$ . Теперь мы готовы считать объём

VAA1C1B = 1VAA1C1CB = 1AC ⋅CC1⋅BC = 2 6

= 1⋅√51-⋅7 ⋅24= 28√51 6

Ответ:

$28√51$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#63888

$ABCD$ — правильная пирамида, в основании которой лежит правильный треугольник $ABC$ со стороной 2. Боковые ребра пирамиды равны 3. Найдите площадь равнобедренного треугольника, одна вершина которого совпадает с $A$ , другая — с серединой $CD$ , а третья лежит на отрезке $BC.$

Показать ответ и решение

Обозначим искомый треугольник $AMN, M$ — середина $CD,N$ на $BC$ . Пусть $T$ — середина $AB$ , тогда $MT$ — высота треугольника. Если $′ M$ — проекция $M$ на высоту $CT$ треугольника $ABC$ , то по теореме Фалеса $′ CM$ равна половине $CO$ , где $O$ — проекция $D$ и одновременно центр описанной окружности (потому что боковые рёбра пирамиды равны), то есть равна половине радиуса описанной около ABC окружности. По теореме синусов $∘ √- R = 2∕(2⋅sin60 )= 2∕ 3$ , тогда

$′ ′ ∘ R- 2- TM = CT − CM = 2sin60 − 2 = √3$ , а

$√------ √-- MM ′ = DO2-=-CD22−R2-= 2√233-$ ,

тем самым $TM = √M-′T2+-M′M2 = ∘23+-4 =∘ 39= √13 12 3 12 2$

Поскольку $AT = AB∕2= 1$ , $AB ⊥(CTD ),$ то по теореме Пифагора

∘---2----2 ∘ 13--- √17- AM = TM + AT = 4 + 1= 2

Возможны случаи:

1) $AM = MN$ . В этом случае $N$ совпадает с $B$ , поскольку пирамида симметрична относительно плоскости, проходящей через середину $CD$ и перпендикулярной $AB$ . Тогда $√-- SAMN = 12 ⋅AB ⋅MT = MT = -123$

2) $AM = AN$ . Но тогда $√ -- AN =-217 >2 =AB = AC$ . Но тогда точка $N$ лежит вне отрезка $BC$ , иначе расстояние от $A$ до неё было бы не больше длины стороны треугольника $ABC$ .

3) $AN =MN$ . Заметим, что $cos∠BCD = BCC∕D2= 13$ . Пусть $CN = x,NB = 2− x$ , запишем теоремы косинусов для $△MCN$ и $△ABN$ , выберем из первого $MN$ , а из второго $AN$ в качестве противолежащих сторон, откуда

AN2 = (2 − x)2+22− 2⋅2(2 − x)⋅ 1 =MN2 =x2 + 9 − 2 ⋅ 3x⋅ 1=⇒ x= 7 2 4 2 3 4

Подставляя $x$ в теорему косинусов, получаем $MN2 = 4196 + 94 − 74 = 5716$ . Посчитаем высоту $h$ из вершины $N$ в треугольнике $ANM$ с учётом $AN = NM$

∘ ------- ∘-- √-- h= ∘NM2--− (AM-∕2)2 = 57− 17= 5= -10 16 16 2 2

Тогда $1 1 √17- √10 √170- SAMN = 2 ⋅h⋅AM = 2 ⋅ 2 ⋅ 2 = 8 .$

Ответ:

$√170 8$ или $√13 2$

Ошибка.
Попробуйте повторить позже

Задача 18#63896

Дан куб $ABCDA ′B′C′D ′$ с основанием $ABCD$ и боковыми рёбрами $AA′$ , $BB′$ , $CC′$ , $DD ′$ . Найдите расстояние между прямой, проходящей через середины рёбер $AB$ и $′ AA$ , и прямой, проходящей через середины рёбер $′ BB$ и $′′ B C$ , если ребро куба равно $1.$

Подсказки к задаче

Подсказка 1

Перед нами встала задача вычислить расстояние между скрещивающимися прямыми, какие способы сделать это вы знаете? Общий перпендикуляр тут не то чтобы очевиден, а вот параллельные плоскости можно попробовать построить! Проведём через середину ВВ' прямую, параллельную прямой проходящей через середины АВ и АА'. Одно сечение прямо перед нами! Назовём эту плоскость α.

Подсказка 2

Второе сечение построить чуть сложнее, но опираясь на знание о том, что параллельные плоскости пересекают третью по параллельным прямым, мы можем сделать и это. Назовём такую плоскость β.

Подсказка 3

Рассмотрим пересечение плоскостей α и (BB'D). В каком отношении плоскость α делит диагональ куба B'D? А что можно сказать про угол между диагональю куба B'D и плоскостью α?

Подсказка 4

Аналогично можно выяснить и про плоскость β: она будет перпендикулярна диагонали куба. Тогда расстояние между α и β равно длине отрезка диагонали куба заключённого между ними. Рассматривая пересечение плоскостей β и (BB'D) можно установить, в каком отношении плоскость β делит нашу диагональ? Немного арифметики и задача решена!

Показать ответ и решение

Пусть $E,F,K,L,M$ — середины рёбер куба $AA ′,$ $AB,$ $B′C ′,$ $B ′B,$ и $B′A′$ соответственно.

$PIC$

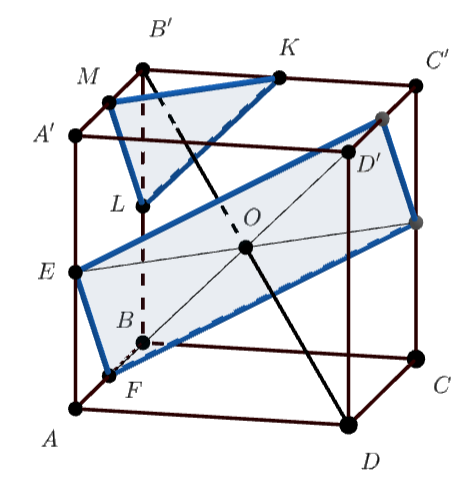
Проведем плоскость через $E,F$ и центр $O$ куба. Данная плоскость перпендикулярна диагонали $B ′D,$ так как $EO||AC,F O||AD′$ , а прямые $AC, AD′$ перпендикулярны $B ′D$ . Так как плоскость $EOF$ проходит через $O,$ она делит $B′D$ в отношении $1 :1.$

Прямая $KL$ лежит в плоскости $KLM$ , которая также перпендикулярна диагонали $B′D.$ При этом плоскость делит диагональ $B ′D$ в отношении $1:5,$ поскольку плоскость $KLM$ проходит через середины ребер $B′C ′,$ $B ′B,$ и $B′A′$ и параллельно плоскости $A′BC ′,$ которая делит $B ′D$ в отношении $1:2.$

Стало быть, искомое расстояние между прямыми равно расстоянию параллельными плоскостями, которые их содержат.

( ) 1− 1 DB ′ = √3∕3= 1∕√3. 2 6

Ответ:

$1∕√3$

Ошибка.
Попробуйте повторить позже

Задача 19#64684

Высота правильной треугольной призмы $ABCA ′B′C′$ с основанием $ABC$ и боковыми рёбрами $AA ′,BB ′,CC′$ равна $1.$ Найдите длину ребра основания, если известно, что $′ ′ AB ⊥ BC .$

Источники: ДВИ - 2022, вариант 223, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Как мы можем применить данную нам перпендикулярность? Кажется, будет удобно построить из точки B' прямую B'B₁, параллельную BC' и взглянуть, на полученную конструкцию. Обозначьте неизвестную сторону основания какой-нибудь переменной и попробуйте выразить всё что тут можно!

Подсказка 2

В основании правильный треугольник, значит у нас есть угол в 60°. Имея в треугольнике две стороны и угол мы сумеем выразить третью сторону: отрезок, соединяющий А с точкой пересечения B'B₁ и плоскости основания. Эту же сторону мы можем выразить при помощи т. Пифагора.

Подсказка 3

Осталось только решить квадратное уравнение, отсечь лишний корень (сторона ведь не может быть отрицательной!) и задача повержена!

Показать ответ и решение

$PIC$

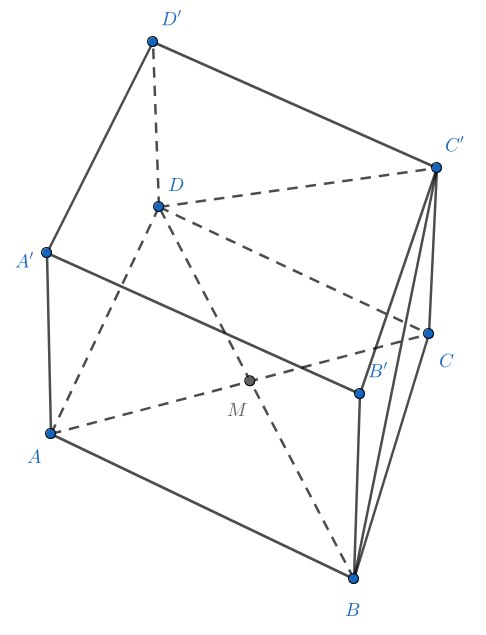
Достроим основания призмы $ABC, A′B ′C ′$ до параллелограммов, получим $ABCD,A ′B′C′D′$ . Получится параллелепипед, в котором $AB ∥DC, AB =CD$ и $AB ′ ∥DC′,AB′ = DC′$ , отсюда $DC′ ⊥ BC ′$ . Кроме того, $BC′ = DC′$ (призма правильная, можно воспользоваться симметрией. Отсюда $△BC ′D$ прямоугольный и равнобедренный. Если $AC ∩ BD = M$ , то $C ′M$ будет высотой этого треугольника, если дополнительно $AB = a$ , то $√- C′M =DM =BM = -32a,CM = AM = a2$ (используем свойства правильного треугольника). Из условия $CC ′ =1$ , применяя теорему Пифагора: $- C′C2+ CM2 = C′M2 ⇐ ⇒ 1+ a2∕4= 3a2∕4 ⇐⇒ a= √2$ .

Ответ:

$√2$

Ошибка.
Попробуйте повторить позже

Задача 20#64685

Дана правильная треугольная пирамида $ABCS$ с основанием $ABC$ и вершиной $S.$ Плоскость $π$ перпендикулярна ребру $AS$ и пересекает рёбра $AS,BS$ в точках $D,E$ соответственно. Известно, что $SD = AD$ и $SE = 2BE.$ Найдите косинус угла между ребром $AS$ и плоскостью основания $ABC.$

Источники: ДВИ - 2022, вариант 225, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Пирамида правильная, поэтому мы чётко знаем куда падает её высота и искомый косинус будет легко выражаться, как только мы узнаем отношение её бокового ребра к ребру основания. Плоскость π перпендикулярна AS. Что в таком случае можно сказать о прямой DE пересечения этой плоскости с плоскостью (SAB)?

Подсказка 2

Итак, DE ⊥ AS. Тогда мы можем, зная положения точек D и E выразить косинус угла при вершине S. Рассмотрите теперь равнобедренный треугольник-грань △ASB: теорема косинусов поможет нам связать его боковые стороны со стороной основания.

Подсказка 3

Пирамида правильная, значит её высота падает в центр основания. Воспользуйтесь свойствами правильного треугольника и найденным в предыдущем пункте соотношением, чтобы выразить искомый косинус.

Показать ответ и решение

$PIC$

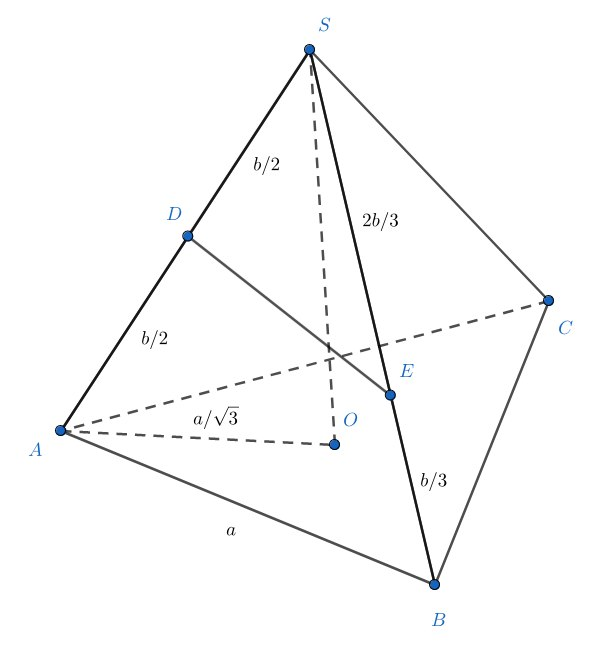
Пусть $a$ — длина ребра основания и $b$ — длина бокового ребра. В прямоугольном треугольнике $SDE$ имеем $SD = 12b$ и $SE = 23b$ . Стало быть, $cos∠ASB = 34$ . Применяя теорему косинусов к треугольнику $ASB$ , получаем, что $a2 =2b2− 2b2⋅ 34$ , откуда $√- b= a 2$ . Пусть $O$ — центр основания. Тогда в прямоугольном треугольнике $ASO$ имеем $√ - AS = b=a 2$ и $√- AO =a∕ 3$ . Стало быть, $√- cos∠SAO = AO∕AS =1∕ 6$ .

Ответ:

$√1- 6$

Предыдущий раздел

Следующий раздел