ГМТ, расположение объектов в пространстве
Ошибка.
Попробуйте повторить позже
В тетраэдре скрещивающиеся рёбра попарно равны. Через середину отрезка
, где
- точка пересечения высот грани
, провели прямую
перпендикулярно плоскости
. Аналогичным образом определили точки
,
и построили
прямые
соответственно для трёх других граней тетраэдра. Докажите, что прямые
пересекаются в одной
точке.
Источники:
Проведём через пару скрещивающихся рёбер тетраэдра две параллельные плоскости. Так же поступим для двух других пар
скрещивающихся рёбер и получим параллелепипед. Диагонали его граней равны между собой, поэтому все грани — прямоугольники, и
параллелепипед прямоугольный. Пусть
— его центр, являющийся также центром описанной сферы тетраэдра
Пусть также
— точки, симметричные
соответственно относительно точки
Докажем, что все построенные прямые проходят
через точку
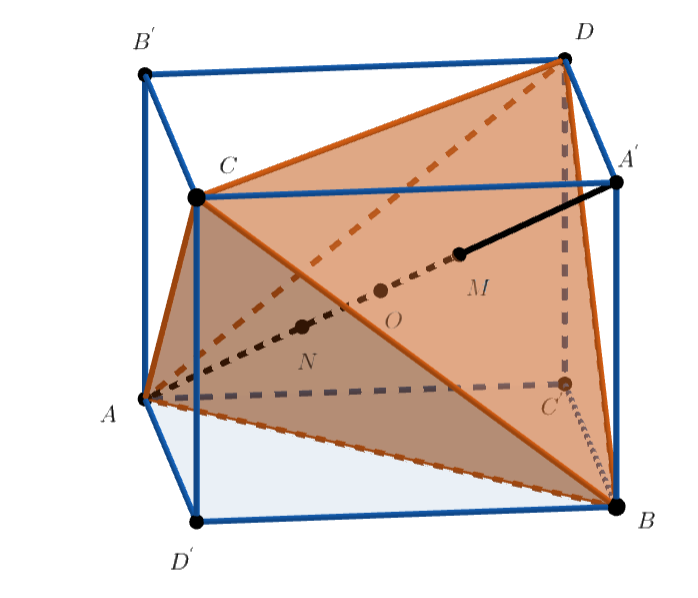
Пусть — центр масс треугольника
. Тогда
То есть точка лежит на диагонали
и делит её в отношении
, считая от вершины
Аналогично центр масс
треугольника
лежит на этой диагонали и делит её в отношении
, считая от вершины
Точка
— середина отрезка
поэтому
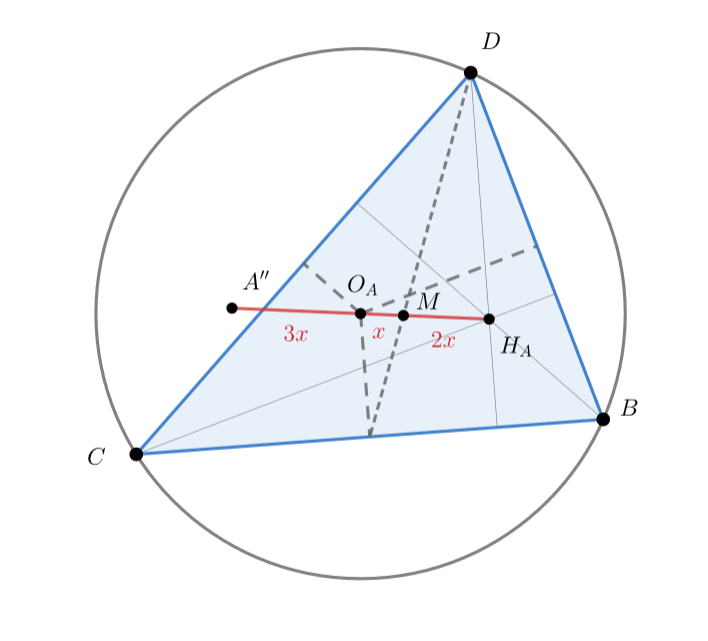
Рассмотрим проекцию на плоскость
— проекция точки
,
— проекция центра
Точка
совпадает с центром
описанной сферы тетраэдра
поэтому
— центр описанной окружности треугольника
Тогда прямая проецируется в прямую Эйлера
треугольника
Пусть
Тогда
(
делит
отрезок
в отношении
, это отношение сохраняется при проецировании). Кроме того,
лежат на одной прямой и
(прямая Эйлера), отсюда
Следовательно,
, а прямая
, перпендикулярная
плоскости
, делит отрезок
пополам, а значит, совпадает с прямой
. Итак, все построенные прямые проходят через точку
.
Ошибка.
Попробуйте повторить позже
B пространстве даны четыре попарно неравных и попарно параллельных отрезка
Докажите, что точки пересечения
продолжений боковых сторон шести трапеций
лежат в одной плоскости.
Источники:
Обозначим через точку пересечения боковых сторон трапеции
Тогда точка
является центром гомотетии с положительным коэффициентом, переводящей отрезок
в отрезок
По теореме о трех центрах гомотетии (теорема о трёх колпаках) точки
лежат на одной прямой. Обозначим эту
прямую через
и докажем, что все такие прямые лежат в одной плоскости.
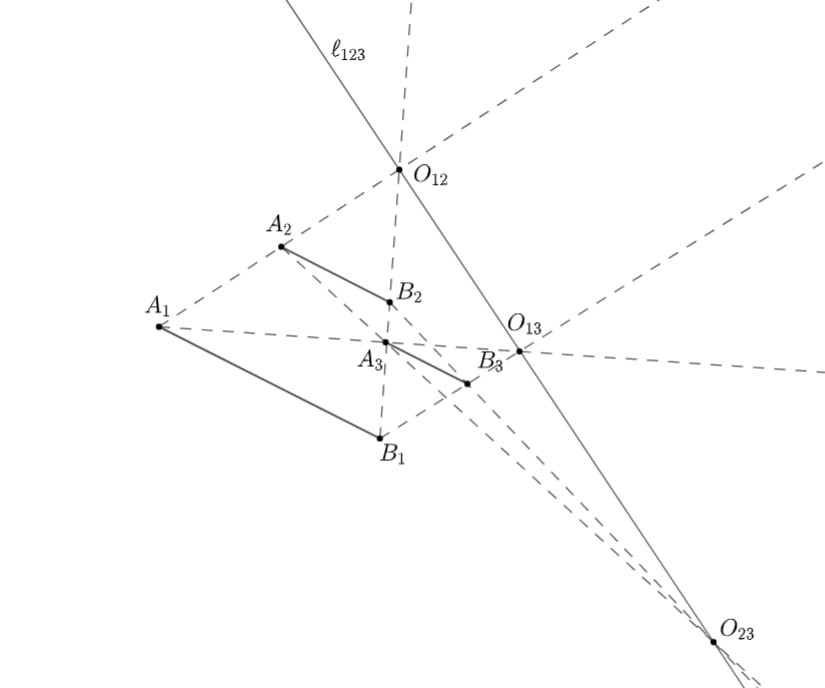
Для этого будем последовательно рисовать их. Сначала проведем прямые и
они лежат в одной плоскости
т.к.
пересекаются в точке
Прямая
пересекает
в точке
а прямую
— в точке
поэтому она также лежит в
плоскости
Наконец, прямая
пересекает прямую
в точке
а прямую
— в точке
так что и она лежит в
плоскости
Итак, все четыре прямые лежат в одной плоскости, и в ней же лежат все шесть точек что и требовалось доказать.
Ошибка.
Попробуйте повторить позже
Многогранник изображен в ортогональной проекции на плоскость
![]()
Докажите, что такой многогранник невозможен.
Источники:
![]()
Прямые и
пересекаются в точке
, лежащей в обеих плоскостях,
и
, то есть на их общей прямой. То же
верно для точек
получающихся как пересечения одноименных рёбер. Значит, все эти точки должны лежать на одной прямой,
что не выполняется.
Если зафиксировать, например, точки , то можно построить изображение вершины
(на рисунке это точка
, которое
не совпадает с изображением точки
на проекции.
Ошибка.
Попробуйте повторить позже
Докажите, что в любую треугольную пирамиду можно вписать единственную сферу.
Пусть эта пирамида . Биссекторы, содержащие рёбра
, пересекаются в одной точке
, которая находится на
одинаковом расстоянии от всех четырёх граней, то есть является центром вписанной в пирамиду сферы. Если нашлась ещё одна сфера с
центром
, то она также обязана лежать в пересечении трёх биссекторов, но такая точка всего одна, поэтому сфера
единственная.
Ошибка.
Попробуйте повторить позже
Дан отрезок Точки
в пространстве выбираются так, чтобы
был правильным треугольником, а
– квадратом.
Докажите, что ортоцентры всех получающихся таким образом треугольников
попадают на некоторую фиксированную
окружность.
Источники:
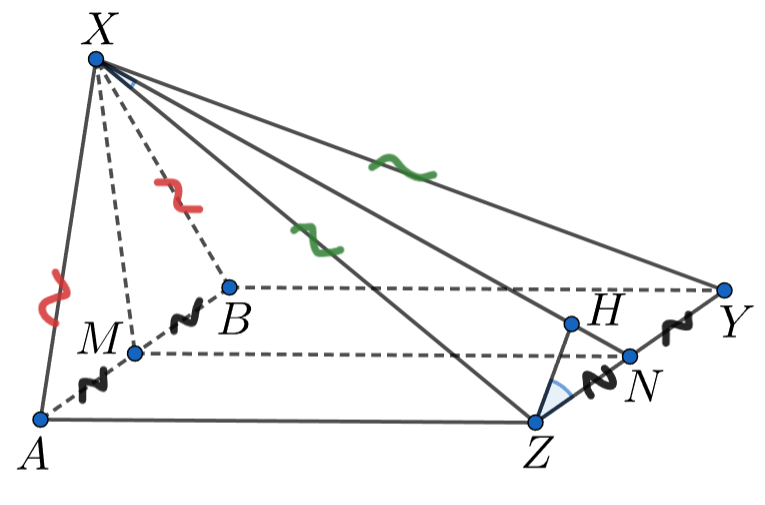
Пусть — середина
— середина
Рассмотрим плоскость
Заметим, что прямая
перпендикулярна прямым
и
а значит она перпендикулярна плоскости
Следовательно,
Нетрудно видеть, что при симметрии
относительно плоскости
отрезок
перейдёт в отрезок
то есть
Таким образом, ортоцентр
треугольника
лежит на отрезке
— серединном перпендикуляре
Покажем, что лежит на окружности
с центром
радиусом
лежащей в плоскости
Для этого определим на
отрезке
точку
такую, что
и точку
— вторичное пересечение прямой
с
Осталось посчитать, что
четырёхугольник
— вписанный, то есть доказать равенство
Пусть длина стороны квадрата и правильного треугольника равна Из подобия треугольников
и
нетрудно получить,
что
Также понятно, что
откуда
Получили
нужное равенство.
Ошибка.
Попробуйте повторить позже
Пусть – середины ребер
соответственно тетраэдра
(a) докажите, что тогда и только тогда, когда
(b) Тетраэдр называется ортоцентрическим, если все его высоты (или их продолжения) пересекаются в одной точке (эту точку называют ортоцентром). Докажите, что тетраэдр ортоцентрический тогда и только тогда, когда отрезки, соединяющие середины противоположных ребер, равны.
(a) Заметим, что , так как
средняя линия в треугольнике
и
средняя линия в треугольнике
.
Аналогично,
. Тогда если
, то в
прямоугольник и
. С другой стороны, если
, то
прямоугольник и
.
![]()
_________________________________________________________________________________________________________________________________________________________________________________
(b) По предыдущему пункту мы знаем, что отрезки, соединяющие середины противоположных ребер, равны тогда и только тогда, когда
,
. Значит, осталось доказать, что тетраэдр
ортоцентрический тогда и только тогда, когда две
пары его противоположных рёбер перпендикулярны.
_________________________________________________________________________________________________________________________________________________________________________________
Если ортоцентрический и
высоты, то рассмотрим плоскость, проходящую через
и
. Она проходит через
и так как
перпендикулярна
и
, то она перпендикулярна
. Значит,
.
_________________________________________________________________________________________________________________________________________________________________________________
Если и
, то рассмотрим плоскость
и
. Значит, это
плоскость перпендикулярна
. Аналогично плоскость
перпендикулярна
. Значит, это одна и та же плоскость и значит
и
пересекаются.
Пусть это точка и через эту точку не проходит
. Аналогично,
и
пересекаются в точке
и
и
пересекаются в точке
. Тогда
и значит,
лежит в плоскости
, но тогда
и
и
Противоречие.
Ошибка.
Попробуйте повторить позже
Тетраэдр называется ортоцентрическим, если все его высоты (или их продолжения) пересекаются в одной точке (эту точку называют ортоцентром).
Докажите, что тетраэдр ортоцентрический тогда и только тогда, когда выполнено одно из следующих условий:
(a) суммы квадратов противоположных ребер равны;
(b) произведения косинусов противоположных двугранных углов равны;
(c) углы между противоположными ребрами равны.
(a)
_________________________________________________________________________________________________________________________________________________________________________________
Если тетраэдр ортоцентрический, высоты и
точка пересечения, то по при проекции на
высоты перейдут в
высоты, а значит,
перейдет в ортоцентр
![]()
Тогда
и
Значит, нам нужно показать, что
Пусть высота в треугольнике
. Тогда
___________________________________________________________________________________________________________________________________________________________________
Если суммы квадратов противоположных ребер равны, то опустим высоту в тетраэдре и раз
, то
. Значит, если опустить перпендикуляры
и
, то
Такое может быть на прямой только, если , что невозможно, либо если
. Значит,
лежит на высоте
.
Аналогично, она лежит на других высотах, и значит,
— ортоцентр. Тогда заметим, что при проекции
перешла в
и
пересекается с
, то и
пересекается с
. Так мы доказали, что любые 2 высоты пересекаются. Если пересекаются любые 2
высоты, то пересекаются все (стоит отдельно это пояснить, но это несложно).
_________________________________________________________________________________________________________________________________________________________________________________
Теорема Бретшнейдера. Пусть и
длины скрещивающихся ребер тетраэдра,
и
двугранные углы при этих ребрах.
Докажите, что величина
не зависит от выбора пары скрещивающихся ребер.
![]()
_________________________________________________________________________________________________________________________________________________________________________________
(b)
_________________________________________________________________________________________________________________________________________________________________________________
Если тетраэдр ортоцентрический, то по прошлому пункту
.
Если двугранные углы при рёбрах и
равны
и
соответственно, то по теореме Бретшнейдера
Поэтому
Мы доказывали выше, что , поэтому тут все сокращается на
и получается
______________________________________________________________________________________________________________________________________________________
Теперь в обратную сторону. Пусть двугранные углы при рёбрах и
равны
и
соответственно и при этом
. Теперь наоборот домножаем на
и применяем факт
.
Поэтому
По теореме Бретшнейдера
Значит, и поэтому тетраэдр
ортоцентрический.
_________________________________________________________________________________________________________________________________________________________________________________
(c)
_________________________________________________________________________________________________________________________________________________________________________________
Если тетраэдр ортоцентрический, то все углы между противоположными ребрами равны .
Если углы между противоположными ребрами равны, то все углы между противоположными рёбрами равны . Предположим,
что
. Тогда
.
Пусть — произведения длин пар противоположных рёбер. Одно из чисел
или
равно сумме двух
других (Доказательство смотри ниже). Так как
, то одно из чисел
или
равно сумме двух других. С другой
стороны, существует невырожденный треугольник, длины сторон которого равны
,
и
(Доказательство смотри
ниже)?!
_________________________________________________________________________________________________________________________________________________________________________________
Факт 1. Пусть и
и
и
- длины пар противоположных рёбер тетраэдра;
- соответственные углы между ними
). Докажите, что одно из трёх чисел
и
- сумма двух других.
_________________________________________________________________________________________________________________________________________________________________________________
Решение. Достроим тетраэдр до параллелепипеда. Тогда и
- диагонали двух противоположных граней параллелепипеда. Пусть
и
- стороны этих граней, причём
. По теореме косинусов
и
, поэтому
. Записав такие равенства для чисел
и
, мы получим требуемое.
_________________________________________________________________________________________________________________________________________________________________________________
Факт 2. Докажите, что для любого тетраэдра существует треугольник, длины сторон которого равны произведениям длин противоположных рёбер тетраэдра.
_________________________________________________________________________________________________________________________________________________________________________________
Пусть длины рёбер и
равны
и
; длины рёбер
и
равны
и
. Проведём через вершину
плоскость, касающуюся описанной около тетраэдра сферы. Рассмотрим тетраэдр
, образованный плоскостями,
и
плоскостью, проходящей через вершину
параллельно плоскости
, и тетраэдр
, образованный плоскостями ,
и плоскостью, проходящей через вершину
параллельно плоскости
.
![]()
Так как - касательная к описанной окружности треугольника
, то
. Кроме того,
,
поэтому
. Следовательно, треугольники
и
подобны, а значит,
, т. е.
. Аналогично
и
. А так как треугольнки
и
подобны, то
, т. е.
. Итак, длины сторон треугольника
, домноженные на
, равны
и
.
Ошибка.
Попробуйте повторить позже
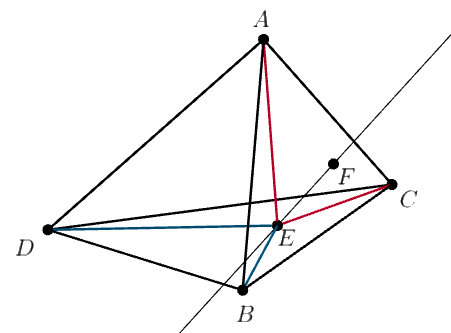
На поверхности тетраэдра нашлись такие точки
и
что
и
Докажите, что
Пусть и
— параллельные плоскости, содержащие ребра
и
обозначим через
расстояние между этими плоскостями. Ясно,
что
С другой стороны, из условия следует, что точки
и
лежат как в плоскости, перпендикулярной
и проходящей
через середину
так и в плоскости, перпендикулярной
и проходящей через середину
(эти плоскости различны, так как
прямые
и
не параллельны). Тогда
— линия пересечения этих плоскостей, поэтому прямая
перпендикулярна
плоскостям
и
Кроме того, поскольку и
лежат на поверхности тетраэдра, то обе эти точки лежат в полосе между
и
Значит,
что и требовалось.
Ошибка.
Попробуйте повторить позже
В пирамиде все боковые рёбра равны. Точка
— середина дуги
описанной окружности треугольника
точка
— середина дуги
описанной окружности треугольника
и т. д., точка
— середина дуги
описанной
окружности треугольника
Докажите, что описанные окружности треугольников
пересекаются в
одной точке.
![]()
Источники:
Заметим, что точки лежат и на сфере с центром в точке
и в одной плоскости. Следовательно, они лежат на окружности
являющейся пересечением сферы с плоскостью. Пусть
— центр этой окружности. Тогда
перпендикулярно плоскости основания
и любая точка на прямой
равноудалена от всех точек окружности
Поэтому на
найдётся и такая точка
для которой
Тогда на сфере
с центром в точке
и радиусом
лежат все вершины пирамиды, а также все окружности
![]()
Следовательно, на этой сфере лежат все точки и
Пусть
— точка на сфере
диаметрально противоположная точке
Покажем, что описанные окружности треугольников
проходят через точку
Поскольку точки
и
лежат на
сфере, достаточно проверить, что они лежат на сфере, достаточно в одной плоскости. Эта плоскость перпендикулярна прямой
и
проходит через точку
В самом деле,
поскольку они опирается на диаметр
сферы
и
поскольку они опираются на диаметры
и
описанных окружностей треугольников
и
Ошибка.
Попробуйте повторить позже
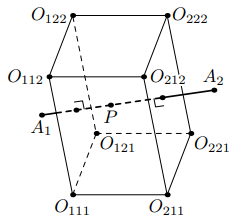
В пространстве даны три отрезка и
, не лежащие в одной плоскости и пересекающиеся в одной точке
. Обозначим
через
центр сферы, проходящей через точки
и
. Докажите, что прямые
и
пересекаются в одной точке.
Источники:
Для любого отрезка серединным перпендикуляром к этому отрезку назовем плоскость, перпендикулярную ему и проходящую через
его середину, т. е. геометрическое место точек, равноудаленных от
и
Пусть — серединный перпендикуляр к отрезку
Тогда
(поскольку на каждой такой сфере лежат обе точки
Легко видеть, что
поскольку обе перпендикулярны прямой
Аналогично определим плоскости
для
и
для
Поскольку шесть выбранных плоскостей попарно параллельны, то они образуют
параллелепипед, осталось заметить, что его вершинами будут точки
Действительно, каждая точка лежит в
плоскостях
(например), откуда и следует нужное. Учитывая, что диагонали параллелепипеда пересекаются в одной точке, всё
доказано.
Ошибка.
Попробуйте повторить позже
В тетраэдре середины всех ребер лежат на одной сфере. Докажите, что его высоты пересекаются в одной точке.
Источники:
Пусть дан тетраэдр а
— середины ребер
и
соответственно. Тогда прямые
и
параллельны
как средние линии треугольников
и
а прямые
и
параллельны
как средние линии треугольников
и
Отсюда немедленно следует, что
— параллелограмм. Но все его вершины лежат на сфере, поэтому он вписанный, т. е.
— прямоугольник. В силу параллельности сторонам прямоугольника прямые
и
перпендикулярны. Аналогично
и
![]()
Докажем, что перпендикулярность противоположных сторон тетраэдра является достаточным условием того, что высоты тетраэдра
пересекаются в одной точке. Построим плоскость, проходящую через ребро перпендикулярно
Высоты тетраэдра, опущенные из
точек
и
лежат в этой плоскости, и значит, пересекаются. Обозначим точку их пересечения через
Высоты из вершин
и
также должны пересекать высоты из вершин
и
но так как они не лежат в плоскости
пересекать их они могут только в точке
Ошибка.
Попробуйте повторить позже
В треугольной пирамиде ребро
перпендикулярно плоскости
. Последовательность точек
строится следующим образом: точка
— центр сферы, описанной около пирамиды
, и для каждого натурального
точка
есть центр сферы, описанной около пирамиды
. Какую длину должно иметь ребро
, чтобы множество
состояло ровно из двух различных точек?
![]()
Применим теорему о трех перпендикулярах. В силу того, что и
, получим, что проекция
на плоскость
перпендикулярна
, то есть
Заметим, что середина гипотенузы - точка
это центр описанной окружности прямоугольного треугольника
.
Аналогично середина гипотенузы
- точка
- центр описанной окружности прямоугольного треугольника
. Тогда если
провести перпендикуляр к плоскости
в точке
и перпендикуляр к плоскости
в точке
, то центр описанной
окружности
пирамиды
- точка пересечения этих перпендикуляров. Но перпендикуляр к плоскости
в точке
совпадает с прямой
. То есть точка
и есть точка
.
При этом на прямой (перпендикуляр к плоскости
в точке
) будут лежать все
в силу того, что
- ГМТ точек
равноудаленных от
То есть точка - центр треугольной пирамиды
- опять-таки должна лежать на прямой
![]()
Хотелось бы добиться того, чтобы (
по очевидным причинам). Но тогда
. То есть середина гипотенузы
равноудалена от точек
. Так же точка
равноудалена от точек
. Но тогда
должен быть ромбом, при
этом его диагональ
должна быть равна стороне. Понятно, что тогда
. Значит, что
, то есть
Ошибка.
Попробуйте повторить позже
Найдите все прямые в пространстве, проходящие через данную точку на данном расстоянии
от данной прямой
.
Источники:
Если точка сама находится на расстоянии от
, то подойдёт вся плоскость
,
(то есть любая прямая
.
Если расстояние
, то таких прямых нет. Иначе это прямая, которая касается цилиндра с осью
и проходит через
.
Чтобы задать такие прямые, построим касательную плоскость к цилиндру, которая содержит
— в силу симметрии их будет две
.
В итоге нам подойдут все
. Нетрудно видеть, что в случае равенства
плоскости просто
совпадают.
Если , то это все
, где
— касательные плоскости к цилиндру с осью
и радиусом
, при этом
.



