Сферы

Воспользуемся формулой радиуса вписанной сферы , где — объём, а — площадь поверхности пирамиды. Объёмы пирамид и равны (грань общая, а вершины и равноудалены от плоскости ); кроме того и (медиана делит площадь треугольника пополам). Значит, равенство сфер, вписанных в пирамиды и , эквивалентно условию или равенству высот, проведённых к стороне в треугольниках и .

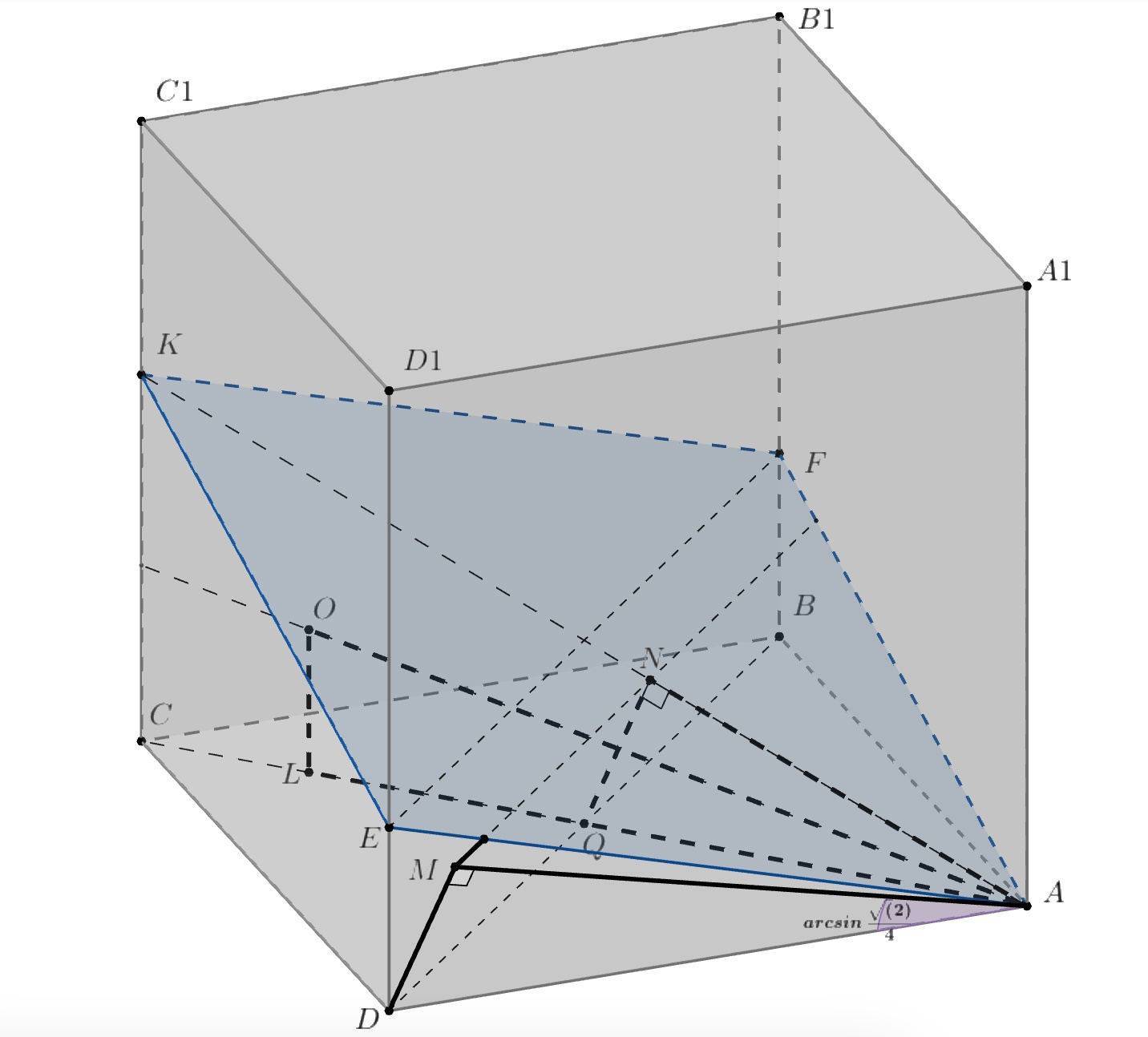
Пусть высота пирамиды, а высота в треугольнике . Объём пирамиды равен , а её высота из вершины равна 3, то есть . Значит, площадь основания пирамиды равна . Тогда сторона основания , а высота треугольника равна 5. Значит, также равно 5. Из прямоугольного треугольника находим , т.е. точка находится на расстоянии 4 от прямой ( лежит на одной из двух прямых, параллельных , на расстоянии 4 от неё). Тем самым, угол между гранями при ребре равен .

Из условия, что грани и взаимно перпендикулярны, следует, что лежит на . Так как , то . Значит или . Тогда или .

Обозначим тетраэдр центр сферы, вписанной в каркас — а саму сферу — Объём тетраэдра равен сумме объёмов маленьких тетраэдров и

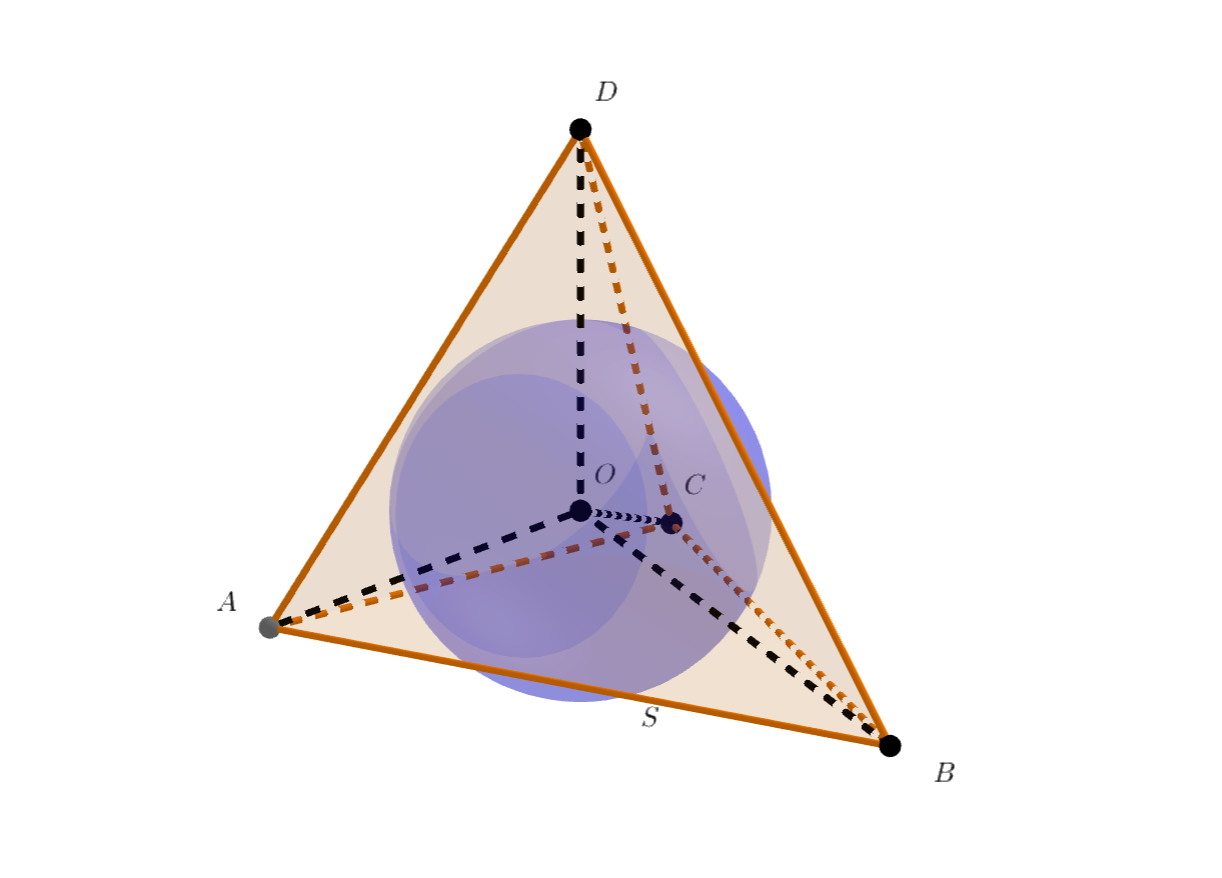
Пересечение и плоскости это вписанная окружность треугольника Обозначим за её центр, тогда — высота тетраэдра Пусть — радиус сферы — радиус вписанной окружности треугольника Тогда выполняется равенство Тогда

где — полупериметр треугольника По неравенству о среднем геометрическом и среднем квадратичном получаем

то есть

Таким образом,

Складывая объёмы четырёх маленьких тетраэдров, получаем

а сумма полупериметров граней это в точности сумма длин рёбер тетраэдра. Значит,

С одной стороны,

С другой стороны,

Поэтому

Заметим, что при данных значениях высот пирамида существует:

На рисунке пирамида вписана в прямоугольный параллелепипед со сторонами 3, 4 и 7. Три высоты совпадают со сторонами, а четвёртая высота будет равна как раз 84/37.

Пусть сфера вписана в тетраэдр Будем её раздувать так, чтобы она оставалась вписана в трёхгранный угол при вершине пока она не коснётся одной из граней тетраэдра Без ограничения общности, полученная сфера касается грани Докажем, что она также касается граней и Из этого последует, что — центры гомотетий с положительными коэффициентами, переводящими в и а в В таком случае точки и лежат на одной прямой.

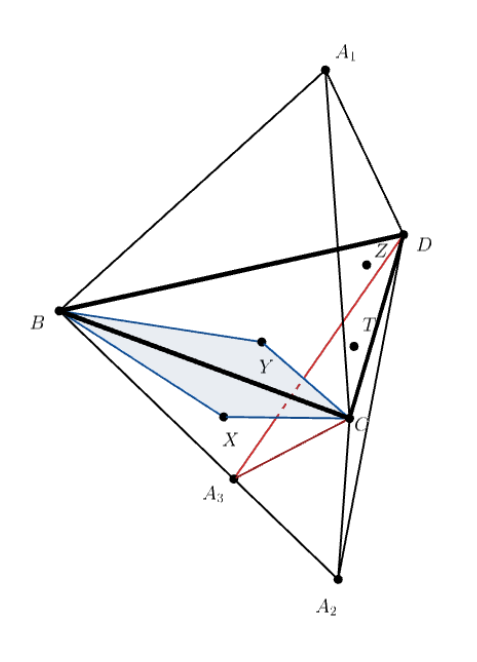
Пусть сфера не касается грани Тогда на ребре найдётся точка такая, что плоскость касается сферы в некоторой точке Обозначим точки касания с плоскостями за соответственно. Тогда имеется четыре пары равных треугольников: и и и и Следовательно,

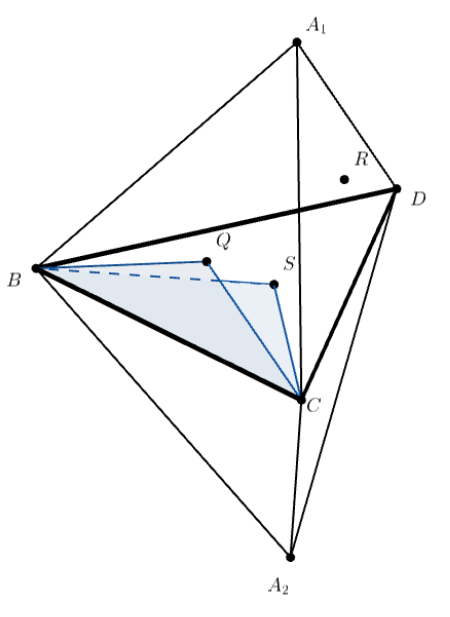
Пусть сфера касается граней в точках соответственно. Тогда треугольники и и и равны. Значит,

Аналогично,

Из равенства крайних членов получаем:

Таким образом,

Но

что противоречит предыдущему равенству. Тем самым, сфера касается грани Аналогично она касается грани что завершает доказательство.

Центр сферы равноудалён от точек на её поверхности, а раз по условию вершины основания принадлежат сфере, то центр сферы является центром описанной около основания окружности.

Пусть сфера пересекает ребро в точке . Тогда равны радиусы Опустим перпендикуляр к ребру , он является медианой равнобедренного треугольника Обозначим сторону основания через и пусть угол Пусть основание перпендикуляра, проведенного из точки на сторону

Находим из правильного треугольника в основании , а так как это линейный угол двугранного угла и равен , то

Также заметим

Тогда получаем

(так как

В итоге так что сфера делит в отношении

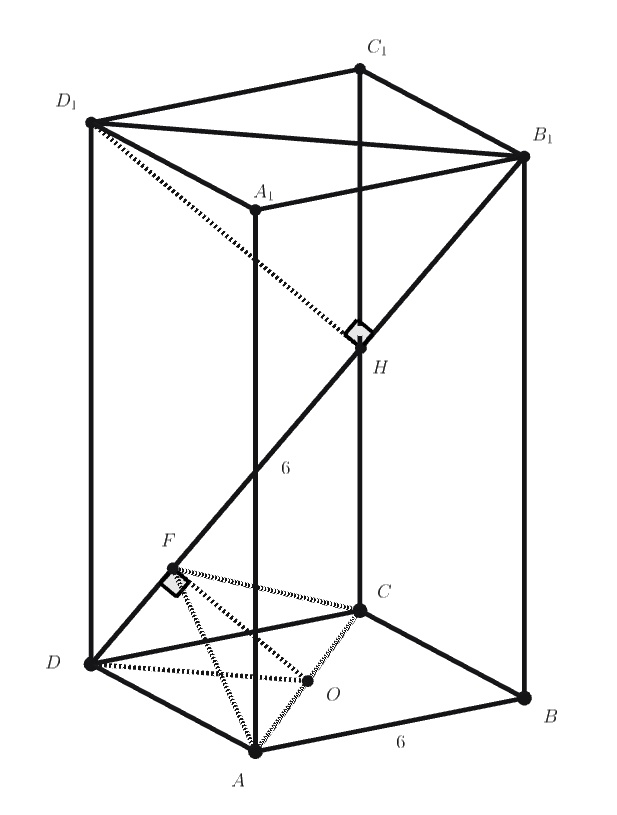
(a) Из соображений симметрии (относительно плоскости плоскость проходит через точку — и, значит, через центр грани Отрезки и — проекции параллельных отрезков и на прямую причём Значит,

(b) Поскольку сфера касается всех боковых граней призмы, её проекция на основание есть окружность, вписанная в это основание. Значит, Кроме того, и — это две параллельные плоскости, касающиеся сферы, поэтому расстояние между ними равно диаметру сферы, то есть Так как этим расстоянием является отрезок поэтому

Обозначим Поскольку — высота прямоугольного треугольника то

и, следовательно, Тогда

и

Получаем уравнение

поскольку

Наконец, высота призмы равна

А объём призмы равен

Обозначив точку пересечения с плоскостью через , получим . В пересечении сферы с плоскостью получается некоторая окружность. Проведём через диаметр этой окружности.

Тогда и — хорды сферы, и по свойству пересекающихся хорд: . Так как , то минимальный радиус окружности больше или равен и значение достигается при , то есть центр этой окружности. Так как , то При этом Значит,

Обозначим через радиус шара, а через и — середины рёбер и соответственно. Плоскость есть центральное сечение шара. Пусть — высота цилиндра, тогда радиус его основания равен . Пусть — точка пересечения отрезков и .

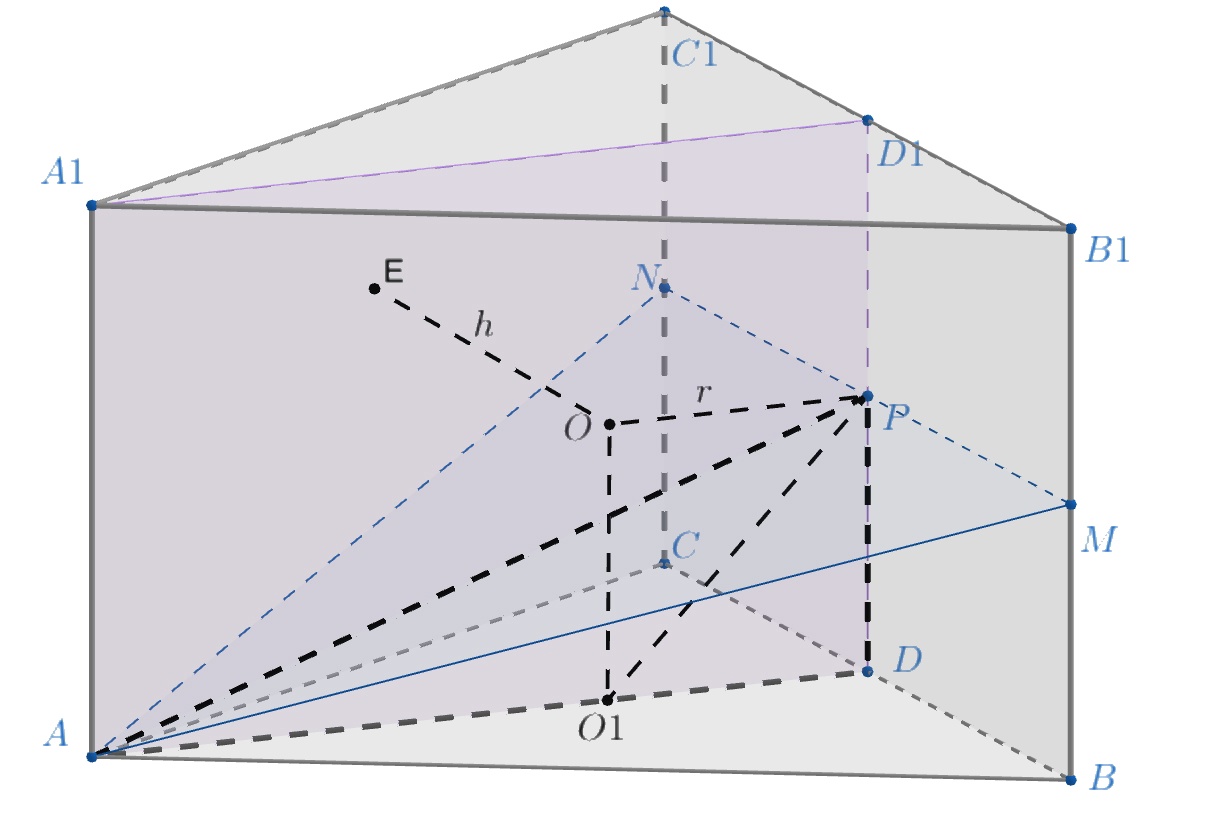
Справедливы соотношения , где — центр шара. Если — проекция точки на основание цилиндра, то из подобия прямоугольных треугольников и получаем

Тогда

Значит, . Площадь боковой поверхности

Первое решение. Утверждение задачи эквивалентно равенству

Значит, ввиду равенств и двух аналогичных, достаточно доказать, что

Пусть — прямая, проходящая через центры сфер и Окружность пересечения этих сфер лежит в плоскости, перпендикулярной так что Это значит, что при повороте вокруг описанная окружность треугольника переходит в себя, и подходящим таким поворотом можно точку перевести в Пусть точки и при этом повороте переходят в и (они тоже лежат на см. рис. слева). Тогда

Равенство доказывается аналогично.

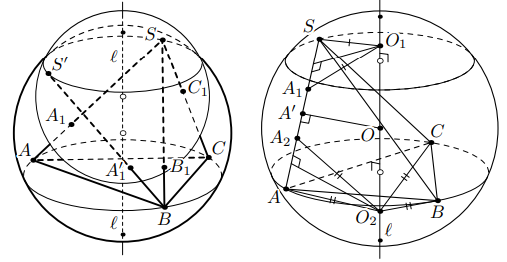
Второе решение. Обозначим через и центры сфер и соответственно. Как и в первом решении, введём прямую проходящую через и тогда

Пусть — точка, симметричная относительно Тогда лежит на откуда обозначим Далее, проекции точек и на симметричны относительно проекции точки т. е. относительно середины отрезка Так как проекция точки является серединой отрезка из симметрии относительно получаем, что проекция точки — это середина отрезка Значит, Аналогично показывается, что Значит, требуемые шесть точек лежат на сфере с центром и радиусом

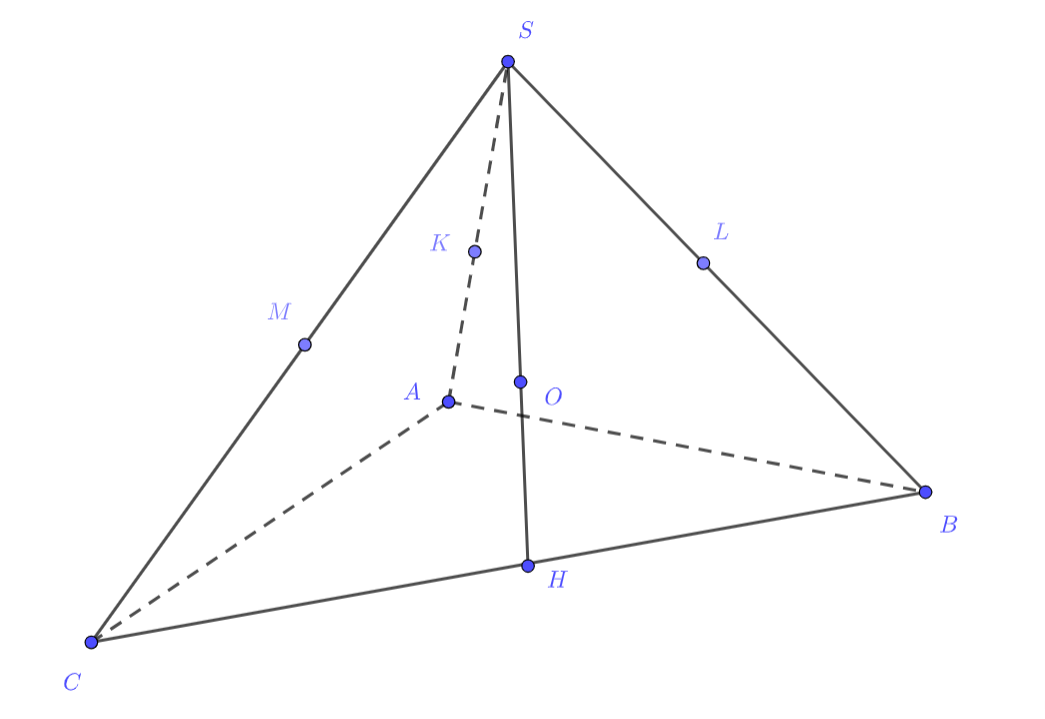
Пусть — центр сферы — основания перпендикуляров, опущенных из точки на ребра соответственно; — высота пирамиды и — радиусы сфер и соответственно.

a) Поскольку точка лежит на серединном перпендикуляре к отрезку она равноудалена от концов этого отрезка, т.е. Аналогично и Значит, поэтому точка является центром сферы . Следовательно, расстояние между центрами сфер равно нулю.

b) Из равенства прямоугольных треугольников , и — общая сторона) следует, что Поскольку точки — это середины боковых рёбер пирамиды, отсюда получаем, что боковые рёбра равны между собой. Тогда высота пирамиды проходит через центр окружности, описанной около основания (действительно, по катету и гипотенузе, откуда ). Но в пирамиде боковые рёбра также равны между собой как радиусы сферы ; значит, и её высота, проведённая из вершины проходит через центр окружности, описанной около основания. Таким образом, высота пирамиды проходит через точку Кроме того, точка является центром окружности, описанной около основания. Поскольку треугольник прямоугольный, — это середина гипотенузы Так как отрезок перпендикулярен плоскости основания, он равен радиусу сферы

Для нахождения соотношения между радиусами рассмотрим прямоугольный треугольник Точка — середина гипотенузы на катете находится точка причём , Треугольники , и равны по катету и гипотенузе, следовательно, Значит, Тогда из треугольника находим, что

c) поэтому треугольник — равносторонний, B равнобедренном треугольнике известны боковые стороны и угол при основании Отсюда находим, что . По теореме Пифагора для треугольника находим, что поэтому объём пирамиды равен

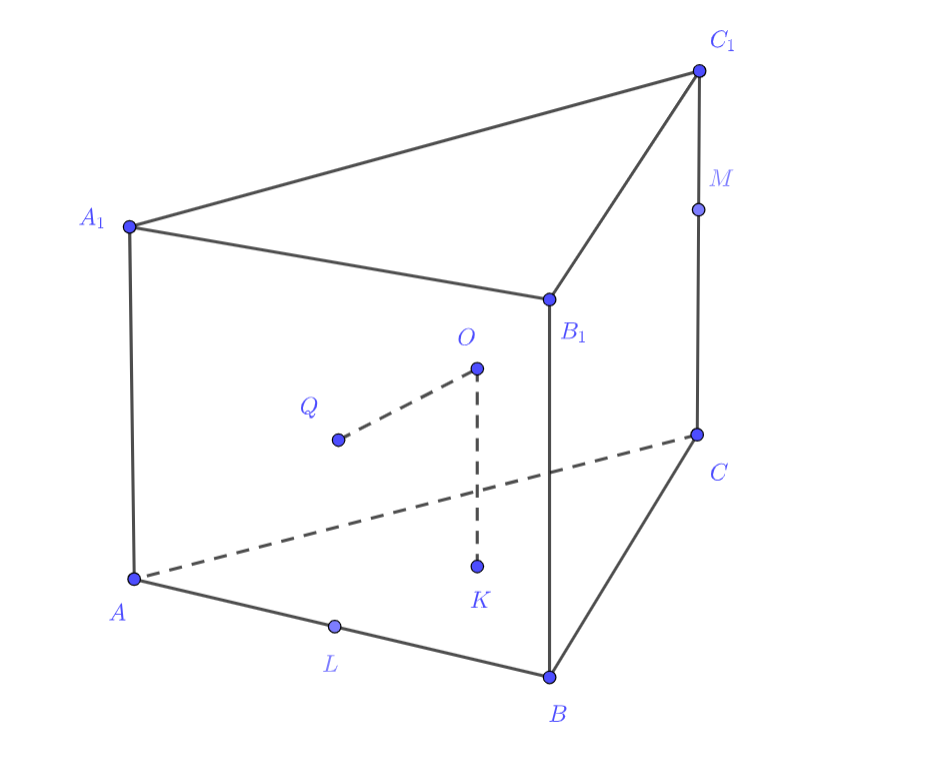
Введём обозначения: — центр грани середина ребра — центр сферы, описанной около пирамиды (т.е. — центр грани ); — центр сферы, описанной около пирамиды .

(a)  3начит, объём пирамиды составляет две трети объёма призмы.

(b) Сторона равностороннего треугольника равна , следовательно, , как радиус описанной окружности.

Рассмотрим прямоугольную трапецию . В ней известны стороны и диагональ По теореме Пифагора из треугольника находим, что Опустим из точки перпендикуляр на отрезок . Тогда

(c) Обозначим Тогда

Отрезки и равны как радиусы сферы. Решая получающееся уравнение, находим, что Тогда площадь поверхности призмы

Пусть у некоторой правильной пирамиды с основанием известно боковое ребро Давайте посчитаем, при какой длине стороны основания пирамида будет обладать наибольшим объемом.

Пусть — центр основания

Теперь это функция от Возьмем производную по Она зануляется при и в этой точке производная меняет свой знак с + на -. Значит, это точка максимума и объем максимальный при .

Вернёмся к задаче. Пирамида, вершинами которой служат точки касания и центр сферы, является правильной треугольной пирамидой с ребром . Значит, чтобы объем был максимальным, нужно добиться того, чтобы сторона ее основания была .

Пусть исходная пирамида с основанием — центр вписанной сферы. точки касания сферы с плоскостями , , соответственно.

Из точек и проведем перпендикуляры к , в силу симметрии они попадут в одну точку .

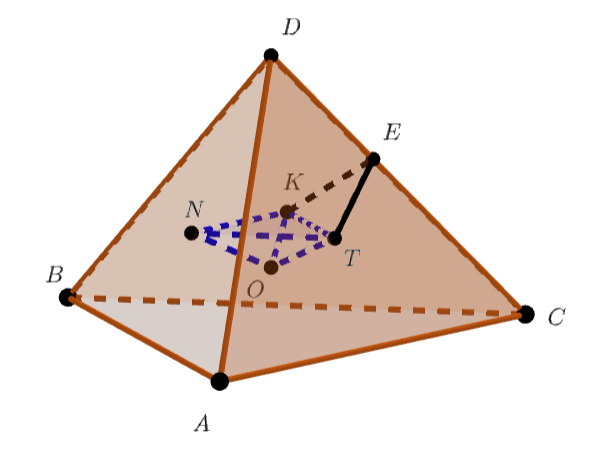
По доказанному ранее и при этом . Значит, , но тогда угол прямой, а его нам и нужно было найти.

Поскольку около параллелепипеда описана сфера, этот параллелепипед — прямоугольный. Обозначим его рёбра, исходящие из одной вершины, через , и . Диагонали параллелепипеда равны диаметру описанной сферы, а объём равен . Из условия задачи следует, что .

По неравенству Коши:

Так как равенство достигается только в случае , то и площадь поверхности:

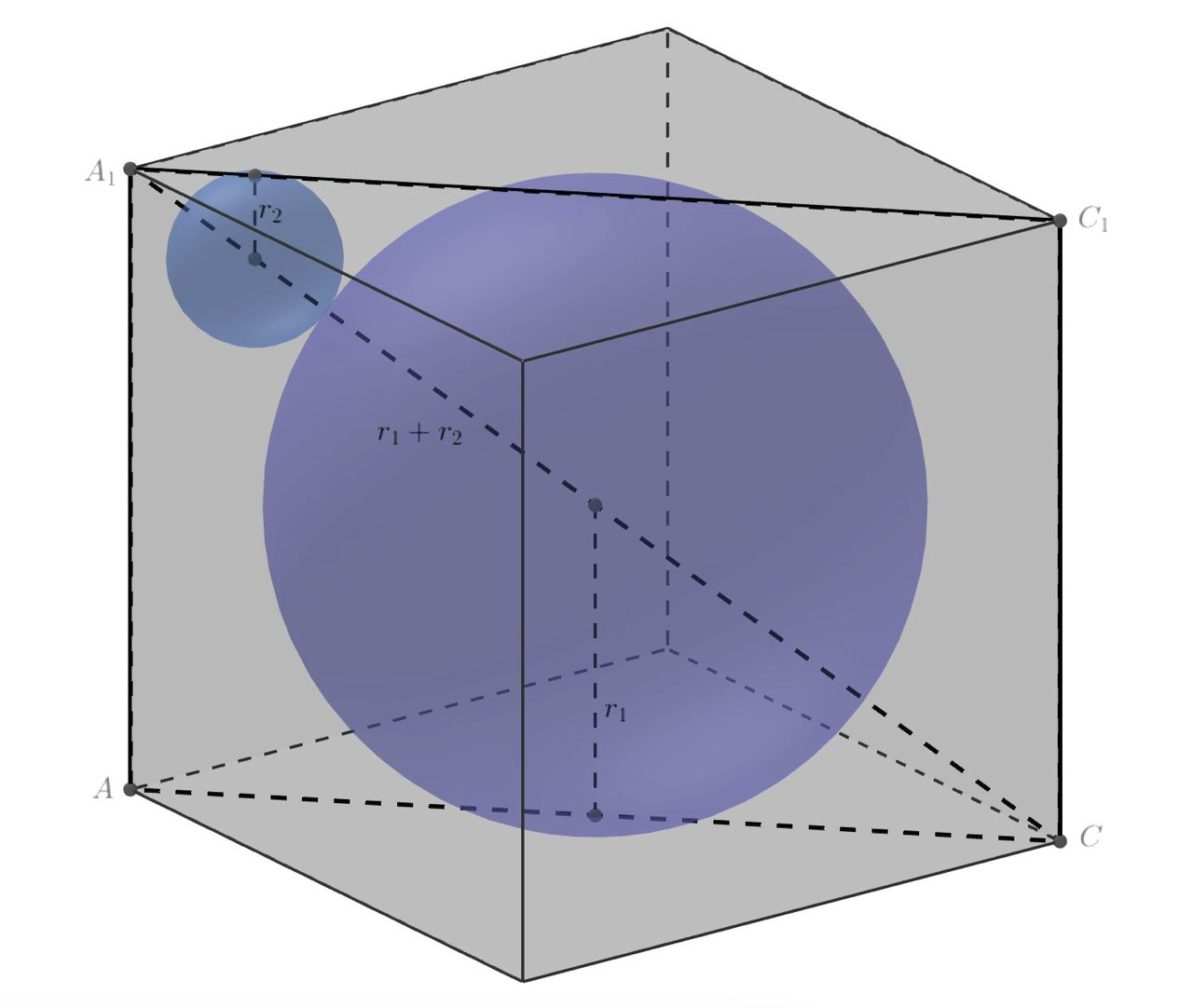
Заметим, что центры обеих сфер лежат на диагонали куба, причём на одной и том же, поскольку касаются разных боковых граней. Действительно, прямая, на которой лежит центр сферы, является биссектрисой трёхгранного угла, поскольку центр куба является центром сферы радиуса , которая касается всех граней, то эта прямая проходит через него. Без ограничения общности, выберем на эту роль диагональ .

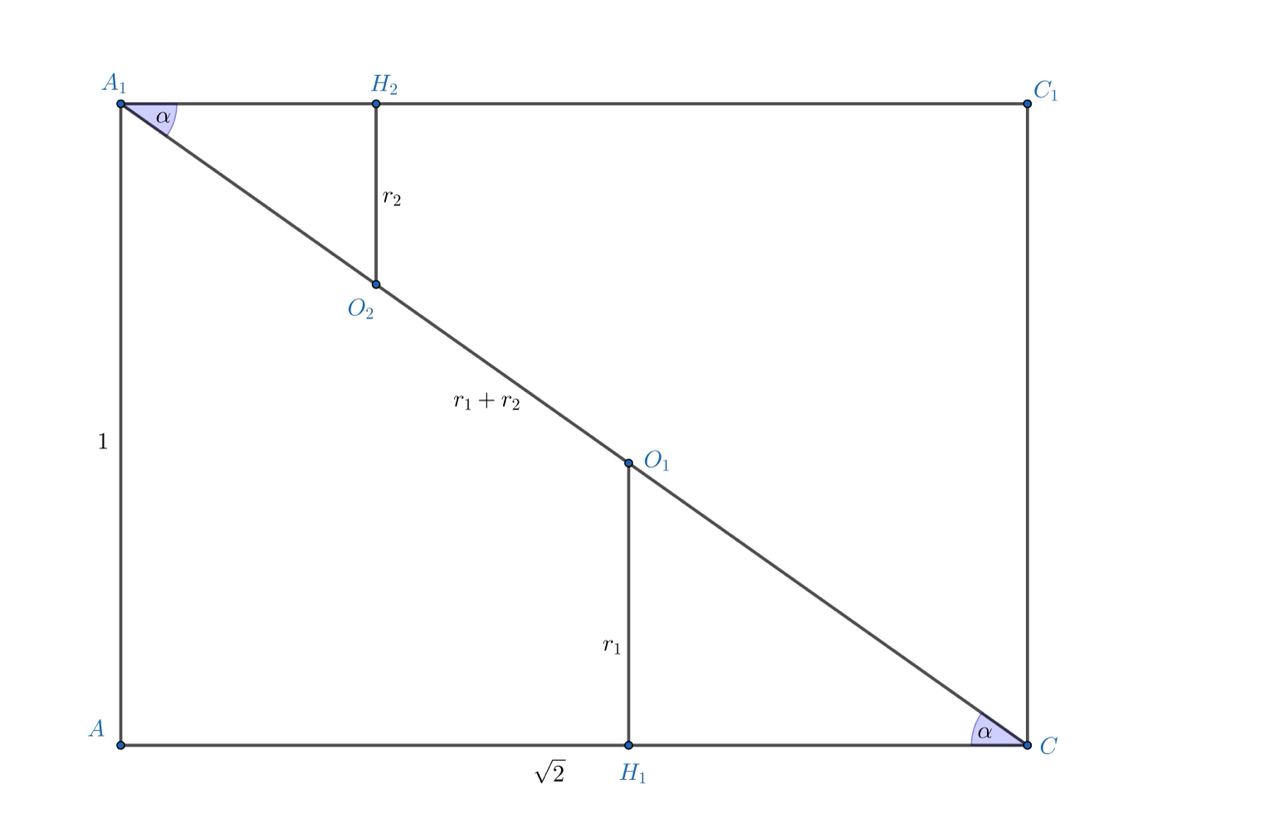
Пусть тогда

Обозначим Пусть и проекции точки на прямые и соответственно. Пусть — радиус сферы.

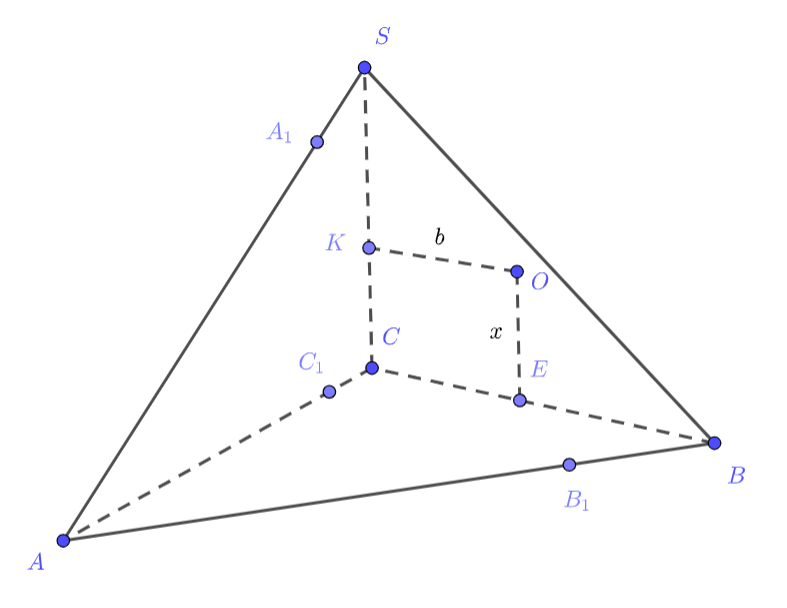
Так как — перпендикуляр к плоскости , а то по теореме о трёх перпендикулярах получаем . Аналогично Из равенства прямоугольных треугольников и следует, что Из равенства прямоугольных треугольников и так как получаем, что Тогда Кроме того, из равенств отрезков касательных, проведённых к сфере из точки следует, что

Для нахождения и выразим из треугольников и Так как и то где Следовательно, откуда получаем

T. e. Тогда .

Так как центр вписанной в пирамиду сферы лежит на её высоте , то образует равные углы с плоскостями . Кроме того, из симметрии следует, что .

Проведём плоскость через перпендикулярно . Пусть эта плоскость пересекает в точке . Аналогично построим точки . Заметим, что треугольники равны, так как они прямоугольные, имеют общий катет , а углы равны, как углы между и плоскостями . Тогда и эти отрезки являются высотами боковых граней пирамиды. Из прямоугольного треугольника находим его высоту .

Рассмотрим треугольник . Пусть . Тогда по теореме косинусов

(1)

Так как и то

Полагая получаем уравнение

Откуда

Тогда из получаем . Так как , то является серединой а из равенства следует, что является высотой треугольника причём .

Пусть — радиус вписанной окружности треугольника .

Тогда . Из равенства

Тогда

Рассмотрим треугольник . Отразив точку симметрично получим точку . Пусть радиус сферы равен . Заметим, что он равен радиусу окружности, вписанной в треугольник . Тогда

 Применим теорему о трех перпендикулярах. В силу того, что и , получим, что проекция на плоскость перпендикулярна , то есть

Заметим, что середина гипотенузы - точка это центр описанной окружности прямоугольного треугольника . Аналогично середина гипотенузы - точка - центр описанной окружности прямоугольного треугольника . Тогда если провести перпендикуляр к плоскости в точке и перпендикуляр к плоскости в точке , то центр описанной окружности пирамиды - точка пересечения этих перпендикуляров. Но перпендикуляр к плоскости в точке совпадает с прямой . То есть точка и есть точка .

При этом на прямой (перпендикуляр к плоскости в точке ) будут лежать все в силу того, что - ГМТ точек равноудаленных от

То есть точка - центр треугольной пирамиды - опять-таки должна лежать на прямой

Хотелось бы добиться того, чтобы ( по очевидным причинам). Но тогда . То есть середина гипотенузы равноудалена от точек . Так же точка равноудалена от точек . Но тогда должен быть ромбом, при этом его диагональ должна быть равна стороне. Понятно, что тогда . Значит, что , то есть

Введем обозначения

А также

По условию . Заметим, что

Значит,

Пусть — радиус вписанной в пирамиду сферы, — высота пирамиды. Тогда

И так как центр вписанной сферы лежит на отрезке , то

С другой стороны, высоты пирамид и , проведённые из общей вершины , равны , поэтому

Откуда

Следовательно,

Плоскость пересечет грань куба по прямой где ребро — в некоторой точке Пусть — середина и основания перпендикуляров, опущенных соответственно из точек и на плоскость Тогда так как и

По условию откуда находим Из треугольника в котором находим и поэтому

Пусть — площадь сечения куба плоскостью тогда где и поэтому

Теперь найдём радиус вписанного шара. Заметим, что центр шара лежит на биссектрисе угла , а проекция точки на грань принадлежат Из треугольника в котором находим

где

Так как

тo

_____________________________________________________________________________________

Замечание.

Искомый радиус можно было также найти, заметив что он равен радиусу шара, вписанного в треугольную пирамиду где — точка пересечения прямых и точка пересечения прямых и используя формулу где — объем пирамиды — её полная поверхность.

Пусть гдс — острый угол:

Тогда двугранные углы при рёбрах и равны между собой и являются острыми (каждый из этих углов углов обозначим

Для доказательства этого утверждения достаточно построить проекцию точки на плоскость затсм опустить из точки перпендикуляры на и и воспользоваться равенством соответствующих прямоугольных треугольников.

Пусть — центр вписанной в призму сферы, и — проекции точки на грани и Тогда где — радиус сферы. Рассмотрим сечения и призмы плоскостями, перпендикулярными рёбрам и Фигуры и являются параллелограммами, каждый из которых описан около окружности радиуса Поэтому фигуры и — ромбы, высота каждого из них равна а острый угол равен Стороны этих ромбов равны соответствующим сторонам прямоугольника и из равенства ромбов следует, что — квадрат.

Пусть — проекция точки на плоскость тогда Проведём через плоскость, перпсндикулярную и пересекающую в точке Тогда и — прямоугольные треугольники, (по условию), . Т. к. отрезок равен стороне ромба, т. е. , то

Последнее выражение в этой цепочке равно высоте ромба .

Заметим ещё, что точка лежит на диагонали квадрата и поэтому

где

и поэтому

Отсюда получаем

где

Рассмотрим, наконец, прямоугольные треугольники и ( — точка, в которой одно из проведённых сечений пересекает ребро , т. е. является вершиной одного из построенных ромбов). Т. к. сфера касается граней двугранного угла при ребре , то

Подставляя найденные значсния и , находим .