05 Статика. Гидростатика - Каталог заданий по ОГЭ

Ошибка.
Попробуйте повторить позже

Задача 1#74170

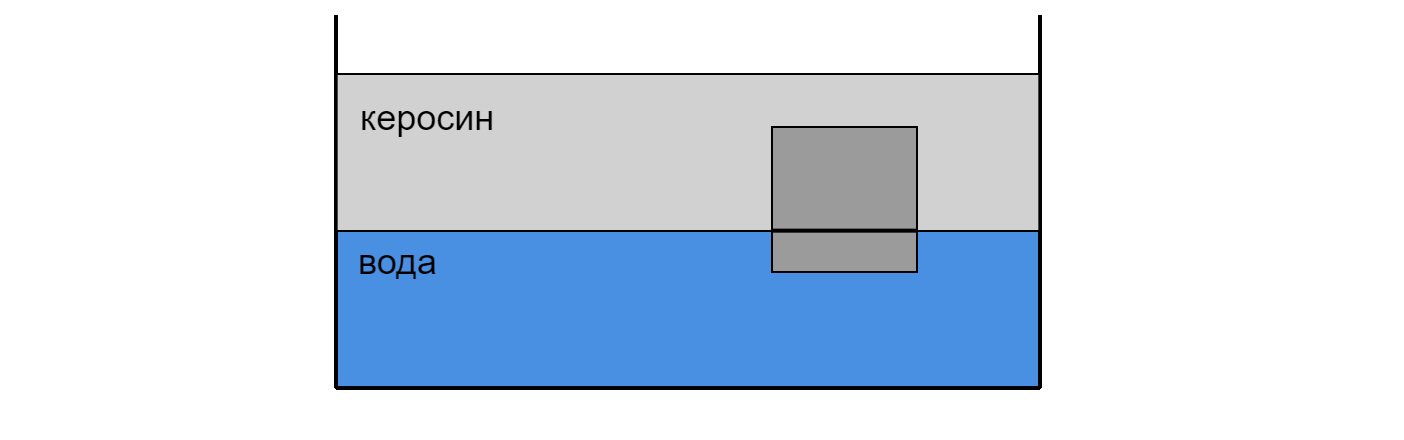
Сплошной кубик плотностью $3 900 кг/м$ плавает на границе раздела воды и керосина, погрузившись в воду на глубину 4 см (см. рисунок). Слой керосина располагается выше, чем верхняя поверхность кубика. Определите длину ребра кубика.

$PIC$

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

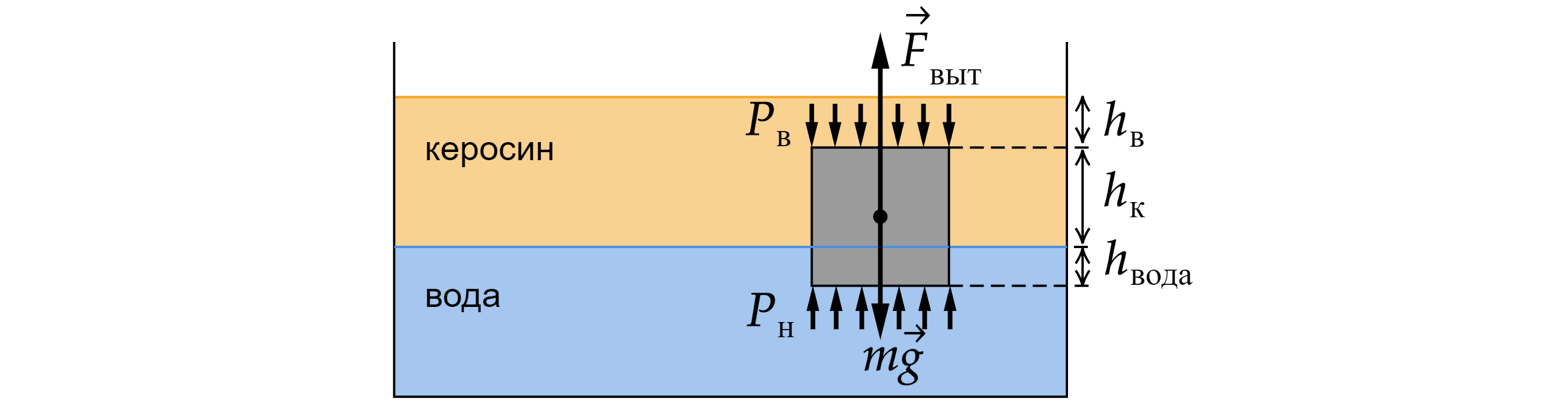
При погружении тела в жидкости на тело начинает действовать выталкивающая сила, которая появляется из-за разности давлений на верхнюю и нижнюю точку тела. Распишем давление на верхнюю и на нижнюю точку тела. Верхняя точка:

P в = P0+ ρкghв

Здесь $P0$ - атмосферное давление, $ρк = 800 кг/м3$ - плотность керосина, $hв$ - расстояние от верхнего уровня жидкости до верхней точки кубика. Нижняя точка:

Pн = P0+ ρкghв+ ρкghк +ρвghвода

Здесь $hк$ - часть ребра, погруженная в керосин, $hвода$ - часть ребра, погруженная в воду, $ρв = 1000 кг/м3$ - плотность воды. Найдем разность давлений:

ΔP =P н− Pв

ΔP =P0 + ρкghв+ ρкghк+ ρвghвода− (P0 +ρкghв)

ΔP = ρкghк+ ρвghвода

Выталкивающая сила и давление связаны формулой $Fвыт =ΔP S$ . Тогда выталкивающая сила равна:

Fвыт = (ρкghк +ρвghвода)S

Здесь $2 S = a$ - площадь основания кубика (площадь любой грани), $a$ - длина ребра кубика. Поскольку в воду погружено $hвода = 4$ см от длины ребра, то высота части, погруженная в керосин равна $hк = a− hвода$ . Поскольку тело находится в состоянии покоя, то выталкивающая сила уравновешивает силу тяжести. Получаем равенство:

Fвыт = mg

Сила тяжести же равна:

mg = ρVg

Здесь $3 ρ= 900 кг/м$ - плотность тела, $3 V = a$ - объём кубика. Получаем:

(ρкghк+ ρвghвода)S = ρV g

С учетом всех выражений выше:

2 3 (ρк(a− hвода)+ ρвhвода)a = ρa

ρк(a − hвода)+ ρвhвода = ρa

ρкa − ρкhвода +ρвhвода = ρa

hвода(ρв − ρк)= ρa− ρкa

hвода(ρв− ρк)= (ρ− ρк)a

Получаем формулу для длины ребра кубика:

hвода(ρв− ρк) a= ---ρ−-ρк---

Считаем:

4(1000− 800) a= --900−-800-- =8 см

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула силы тяжесты, формула силы Архимеда, формула объёма)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 2#74328

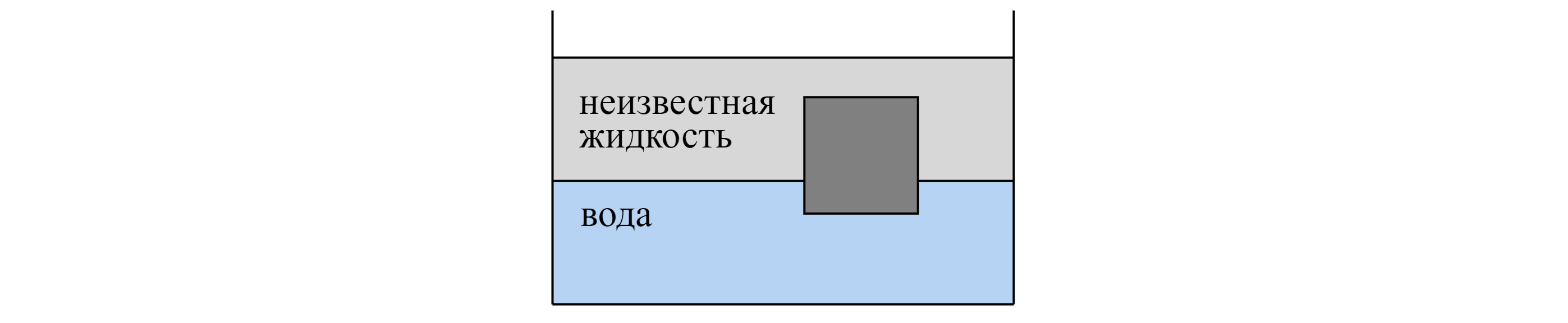
Сплошной кубик с ребром 10 см плавает на границе раздела воды и неизвестной жидкости, плотность которой меньше плотности воды, погрузившись в воду на 2 см (см. рисунок). Плотность вещества, из которого изготовлен кубик, равна 840 кг/м $3$ . Свободная поверхность неизвестной жидкости располагается выше, чем верхняя поверхность кубика. Определите плотность неизвестной жидкости.

$PIC$

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

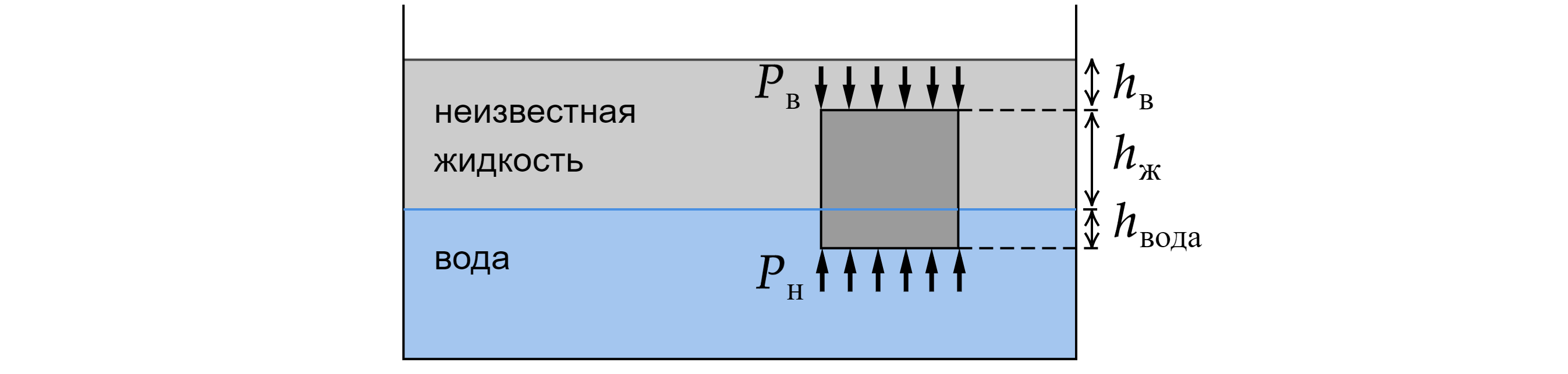
При погружении тела в жидкости на тело начинает действовать выталкивающая сила, которая появляется из-за разности давлений на верхнюю и нижнюю точку тела. Распишем давление на верхнюю и на нижнюю точку тела. Верхняя точка:

Pв = P0+ ρжghв

Здесь $P0$ - атмосферное давление, $ρж$ - плотность жидкости, $hв$ - расстояние от верхнего уровня жидкости до верхней точки кубика. Нижняя точка:

Pн = P0+ ρжgh в+ ρжgh ж+ ρвghвода

Здесь $hж$ - часть ребра, погруженная в жидкость неизвестной плотности, $hвода$ - часть ребра, погруженная в воду, $ρв = 1000$ кг/м $3$ - плотность воды Найдем разность давлений:

ΔP =P н− Pв

ΔP = P0+ ρжghв+ ρжghж+ ρвghвода− (P0+ ρжghв)

ΔP =ρжgh ж+ ρвghвода

Выталкивающая сила и давление связаны формулой $Fвыт =ΔP S$ Тогда выталкивающая сила равна:

Fвыт = (ρжghж + ρвghвода)S

Здесь $2 S = a$ - площадь основания кубика (площадь любой грани), $a$ - длина ребра кубика. Поскольку в воду погружено $hвода = 2$ см от длины ребра, то высота части, погруженная в неизвестную жидкость равна $hк = a− hвода$ . Поскольку тело находится в состоянии покоя, то выталкивающая сила уравновешивает силу тяжести. Получаем равенство:

Fвыт = mg

Сила тяжести же равна:

mg = ρVg

Здесь $ρ= 840$ кг/м $3$ - плотность тела, $3 V = a$ - объём кубика. Получаем:

(ρкghк+ ρвghвода)S = ρV g

С учетом всех выражений выше:

2 3 (ρж(a − hвода)+ ρвhвода)a =ρa

ρж(a − hвода) +ρвhвода = ρa

ρжa − ρжh вода+ ρвhвода = ρa

hвода(ρв− ρж)= ρa− ρжa

hводаρв− hводаρж =ρa − ρжa

hводаρв− ρa= hводаρж − ρжa

hводаρв − ρa = (hвода − a)ρж

hводаρв− ρa ρж = --hвода−-a-

ρж = ρa-− hводаρв a− hвода

Считаем:

840⋅10− 2⋅1000 3 ρж = -----10−-2----= 800 кг/м

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула силы тяжесты, формула силы Архимеда, формула объёма)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 3#76443

Сплошной кубик с ребром 20 см плавает на границе раздела воды и керосина (см. рисунок). Плотность вещества, из которого изготовлен кубик, равна 850 кг/м³. Слой керосина располагается выше, чем верхняя поверхность кубика. Определите, на какую глубину кубик погружён в воду.

$PIC$

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

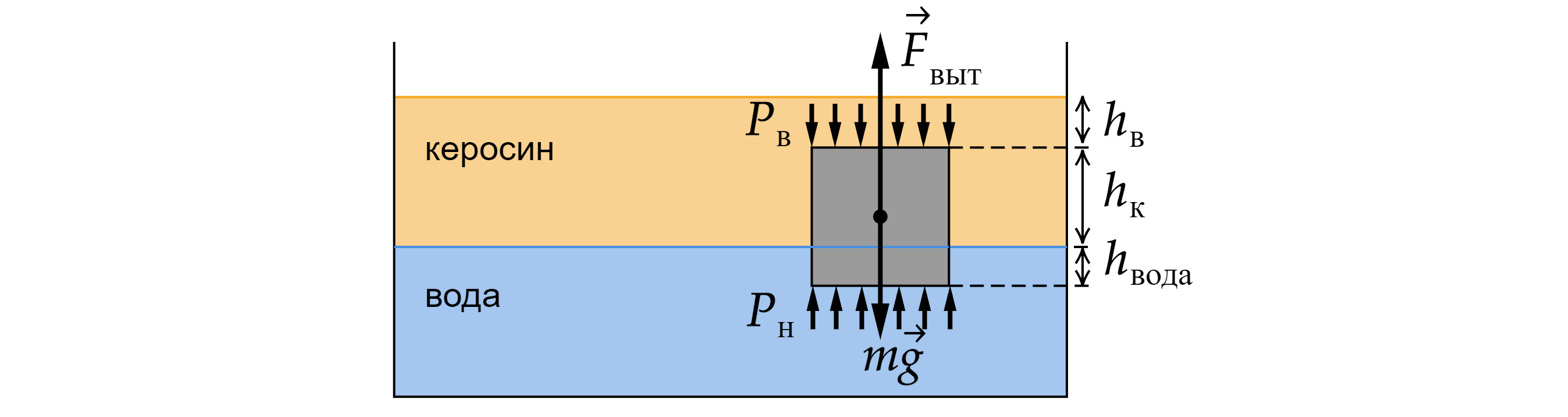
При погружении тела в жидкости на тело начинает действовать выталкивающая сила, которая появляется из-за разности давлений на верхнюю и нижнюю точку тела. Распишем давление на верхнюю и на нижнюю точку тела. Верхняя точка:

P в = P0+ ρкghв

Здесь $P0$ - атмосферное давление, $ρк = 800$ кг/м $3$ - плотность керосина, $hв$ - расстояние от верхнего уровня жидкости до верхней точки кубика. Нижняя точка:

Pн = P0+ ρкghв+ ρкghк +ρвghвода

Здесь $hк$ - часть ребра, погруженная в керосин, $hвода$ - часть ребра, погруженная в воду, $ρв = 1000$ кг/м $3$ - плотность воды Найдем разность давлений:

ΔP =P н− Pв

ΔP =P0 + ρкghв+ ρкghк+ ρвghвода− (P0 +ρкghв)

ΔP = ρкghк+ ρвghвода

Выталкивающая сила и давление связаны формулой $Fвыт =ΔP S$ Тогда выталкивающая сила равна:

Fвыт = (ρкghк +ρвghвода)S

Здесь $2 S = a$ - площадь основания кубика (площадь любой грани), $a$ - длина ребра кубика. Поскольку в воду погружено $hвода = 4$ см от длины ребра, то высота части, погруженная в керосин равна $hк = a− hвода$ . Поскольку тело находится в состоянии покоя, то выталкивающая сила уравновешивает силу тяжести. Получаем равенство:

Fвыт = mg

Сила тяжести же равна:

mg = ρVg

Здесь $ρ= 850$ кг/м $3$ - плотность тела, $3 V = a$ - объём кубика. Получаем:

(ρкghк+ ρвghвода)S = ρV g

С учетом всех выражений выше:

2 3 (ρк(a− hвода)+ ρвhвода)a = ρa

ρк(a − hвода)+ ρвhвода = ρa

ρкa − ρкhвода +ρвhвода = ρa

hвода(ρв − ρк)= ρa− ρкa

hвода(ρв− ρк)= (ρ− ρк)a

Получаем формулу для глубины погружения в воду:

a(ρ− ρк) hвода =-ρв−-ρк-

Считаем:

20(850− 800) hвода = -1000−-800--= 5 см

Решение из сборника
Так как кубик покоится, то сумма всех сил, действующих на кубик равна нулю. Вниз действует сила тяжести $mg$ , а вверх две силы Архимеда (со стороны керосина и со стороны воды) Сила Архимеда равна:

Fарх = ρgVп

где $ρ$ – плотность жидкости, $Vп$ – объём погружённого тела.
Запишем второй закон Ньютона:

mg − ρ1gV1 − ρ2gV2 = 0,

где $ρ1 = 800$ кг/м $3$ – плотность керосина; $ρ2 =1000$ кг/м $3$ – плотность воды.
Объём можно найти по формуле:

V = aS,

где $a$ – высота кубика, $S$ – площадь поперечного сечения.
Пусть высота части, которая погружена в воде $h$ и $ρт = 850$ кг/м $3$ .
Отсюда можно найти массу кубика:

ρтgaS = ρ1gS(a− h)+ρ2gSh,

ρ a− ρa 850⋅0,2− 800⋅0,2 h = -тρ-−-ρ1-= ----1000-− 800---= 0,05 м =5 см. 2 1

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула силы тяжесты, формула силы Архимеда, формула объёма)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 4#44969

Сплошной кубик с ребром 10 см плавает на границе раздела воды и керосина, погружаясь в воду на 2 см (см. рисунок). Свободная поверхность керосина располагается выше, чем верхняя поверхность кубика. Определите плотность вещества, из которого изготовлен кубик

$PIC$

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

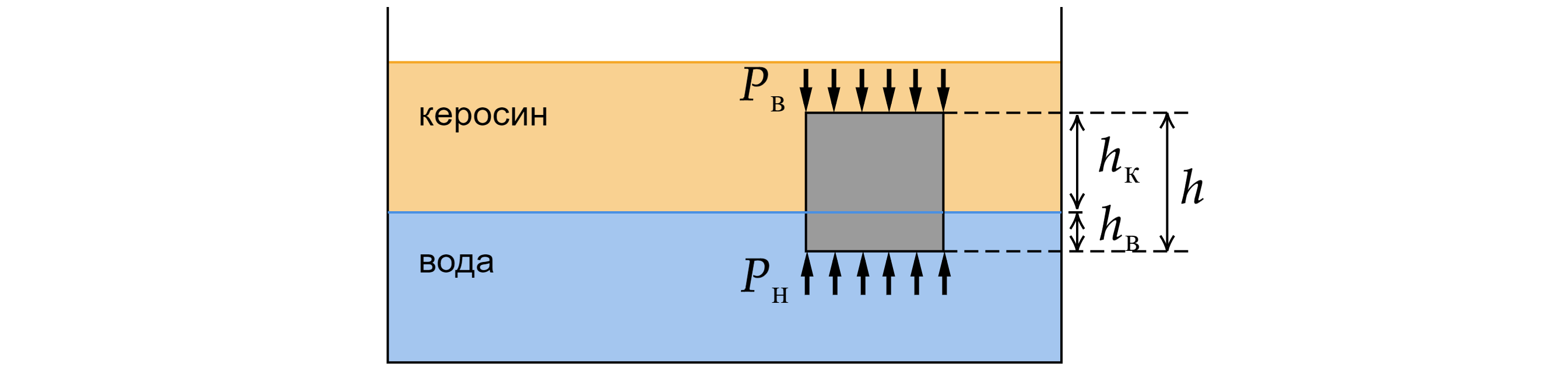
Так как кубик покоится, то сумма всех сил, действующих на кубик равна нулю. Вниз действует сила тяжести $mg$ , а вверх две силы Архимеда (со стороны керосина и со стороны воды) Сила Архимеда равна:

Fарх = ρgVп

где $ρ$ – плотность жидкости, $Vп$ – объём погружённого тела.
Запишем второй закон Ньютона:

mg − ρ1gV1 − ρ2gV2 = 0,

где $ρ1 = 800$ кг/м $3$ – плотность керосина; $ρ2 = 1000$ кг/м $3$ – плотность воды.

V1 = hкS

V2 = hвS

Объём можно найти по формуле:

V = hS,

где $h$ – высота кубика, $S$ – площадь поперечного сечения.
Отсюда можно найти массу кубика:

m = ρ1V1 + ρ2V2 = 800 кг/м3 ⋅0,1 м⋅0,1 м⋅(0,1 м− 0,02 м )+ 1000 кг/м3 ⋅0,1 м ⋅0,1 м ⋅0,02 м = 0,84 кг

Плотность равна:

m- 0,84-кг 3 ρ = V = 0,13 м3 = 840 кг/м

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула силы Архимеда, формула силы тяжести, условие плавания тела)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 5#105101

Сплошной металлический цилиндр, подвешенный к динамометру, поочередно полностью опускают сначала в воду, а затем в керосин. Показания динамометра в первом случае составляют 3,4 Н, а во втором – 3,8 Н. Чему равна плотность металла, из которого изготовлен цилиндр?

Источники: Банк ФИПИ

Показать ответ и решение

Пусть плотность металла $ρм$ , плотность воды $3 ρв = 1000 кг/м$ , плотность керосина $3 ρк =800 кг/м$ При нахождении в жидкостях на цилиндр действуют две силы: сила Архимеда и сила тяжести.
Согласно закону Архимеда, выталкивающая сила равна

Fарх = ρжgVп,

где $ρж$ - плотность жидкости, $Vп$ - объём тела, погруженной в жидкость.

$PIC$

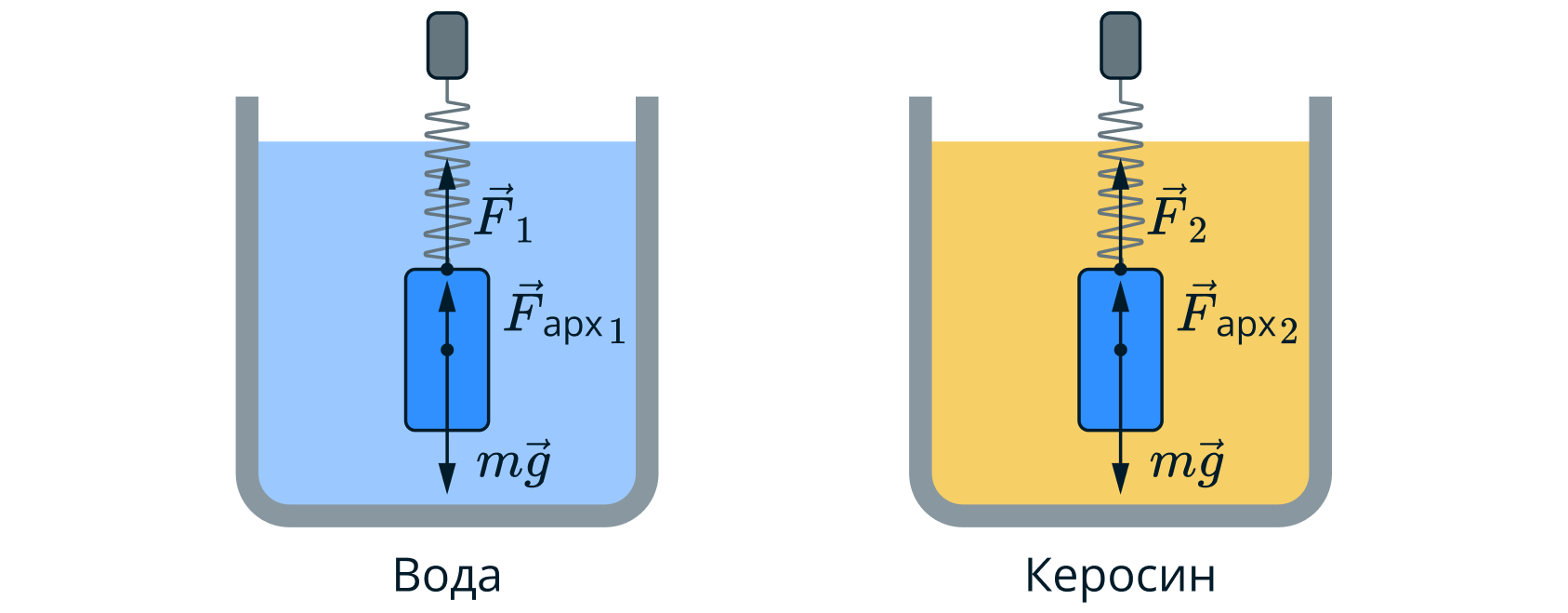
Тогда показания динамометров равны

F1 = ρмgV − ρвgV = 3,4 H, (1)

F2 = ρмgV − ρкgV = 3,8 H,

Тогда

F2− F1 = gV(ρв− ρк),

F2− F1 0,4 V = g(ρв−-ρк) = 10-⋅(1000−-800) = 0,0002 м3.

Тогда плотность металла из (1)

ρм = F1-+ρвgV-= F1-+ ρв =--3,4---+ 1000 = 2700 кг/м3. gV gV 10⋅0,0002

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 6#105102

Сплошной металлический цилиндр, подвешенный к динамометру, поочередно полностью опускают сначала в воду, а затем в спирт. Показания динамометра в первом случае составляют 7,2 Н, а во втором – 7,4 Н. Чему равна плотность цилиндра?

Источники: Банк ФИПИ

Показать ответ и решение

Пусть плотность металла $ρм$ , плотность воды $3 ρв = 1000 кг/м$ , плотность спирта $3 ρс =800 кг/м$ При нахождении в жидкостях на цилиндр действуют две силы: сила Архимеда и сила тяжести.
Согласно закону Архимеда, выталкивающая сила равна

Fарх = ρжgVп,

где $ρж$ - плотность жидкости, $Vп$ - объём тела, погруженной в жидкость.

$PIC$

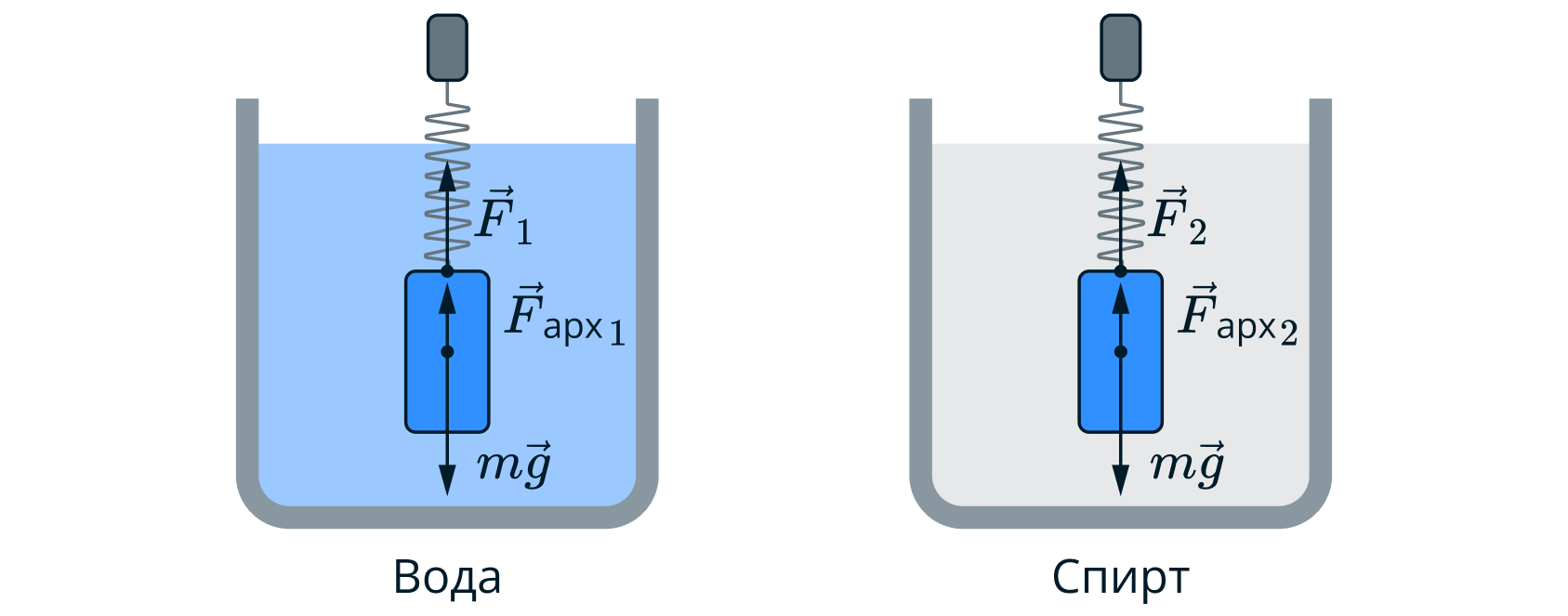
Тогда показания динамометров равны

F1 = ρмgV − ρвgV = 7,2 H, (1)

F2 = ρмgV − ρсgV = 7,4 H,

Тогда

F2− F1 = gV (ρв− ρс),

F2− F1 0,2 V = g(ρв−-ρк) = 10-⋅(1000−-800) = 0,0001 м3.

Тогда плотность металла из (1)

ρм = F1-+ρвgV-= F1-+ ρв =--7,2---+ 1000 = 8200 кг/м3. gV gV 10⋅0,0001

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 7#41562

Медный шар, в котором имеется воздушная полость, опущен в керосин. Наружный объём шара 0,1 м³. Найдите объём воздушной полости, если шар плавает на поверхности керосина, погрузившись в него на 0,89 своего объёма.

Источники: Банк ФИПИ | Камзеева 2024

Показать ответ и решение

$PIC$

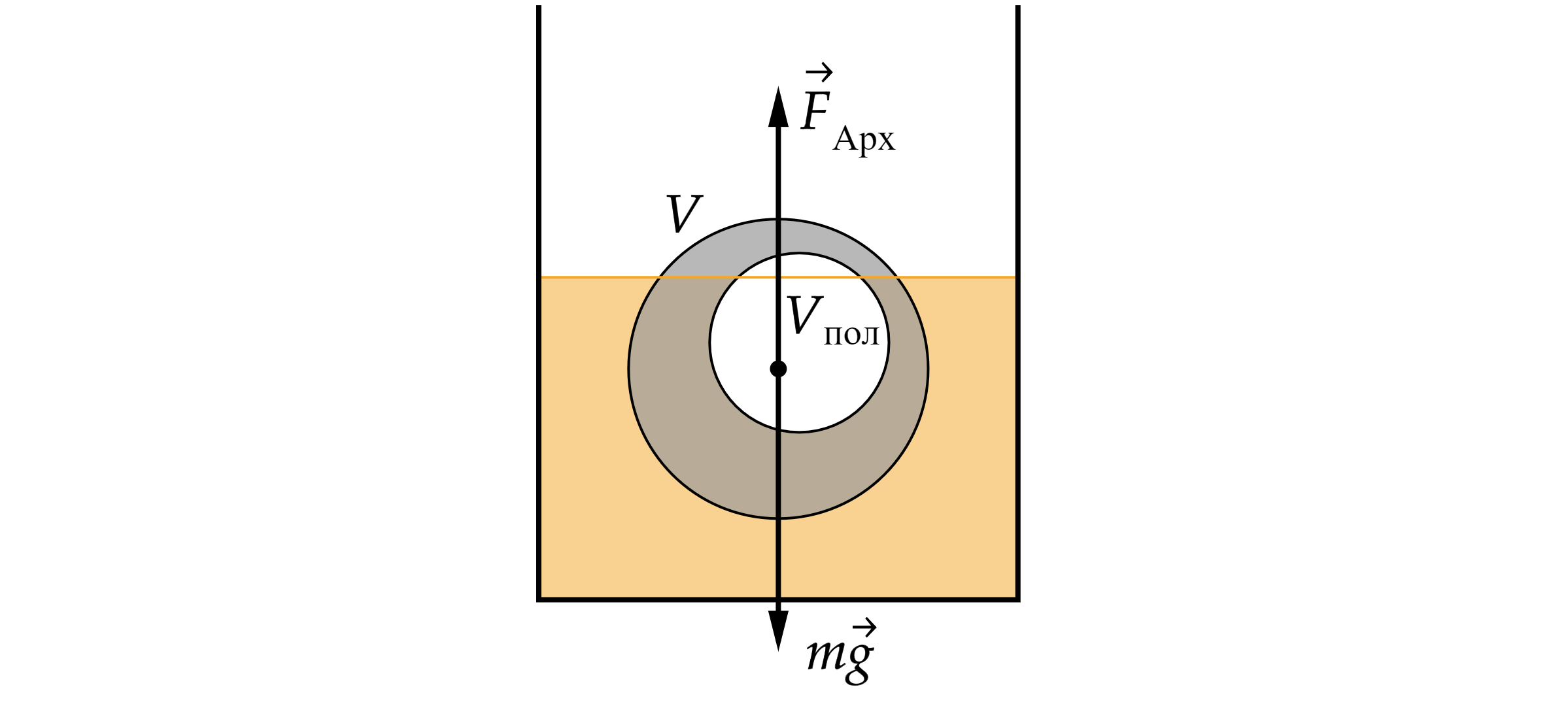
Сила Архимеда равна:

Fарх = ρgVп = ρg⋅0,89V,

где $ρ = 800$ кг/м $3$ – плотность керосина, $Vп$ – объём погружённого тела, $V$ – объём тела.
Так как тело плавает в воде, то выполнено равенство:

Fарх = mg = ρg ⋅0,89V

Масса тела из алюминия равна

m = ρm (V − Vпол)

где $ρm = 8900$ кг/м $3$ – плотность меди; $Vпол$ – объем воздушной полости. Подставляя данное выражение в первую формулу, имеем:

0,89ρ 3 0,89ρgV = ρmg(V − Vпол) ⇒ Vпол = V − V ρm = 0,092 м

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула силы Архимеда, формула силы тяжести, условие плавания тела (равенство силы Архимеда и силы тяжести))

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 8#41703

Тело из алюминия, внутри которого имеется воздушная полость, плавает в воде, погрузившись в воду на 0,54 своего объёма. Объём тела (включая полость) равен 0,04 м³. Найдите объём воздушной полости. Массой воздуха в полости пренебречь.

Источники: Банк ФИПИ | Камзеева 2024

Показать ответ и решение

$PIC$

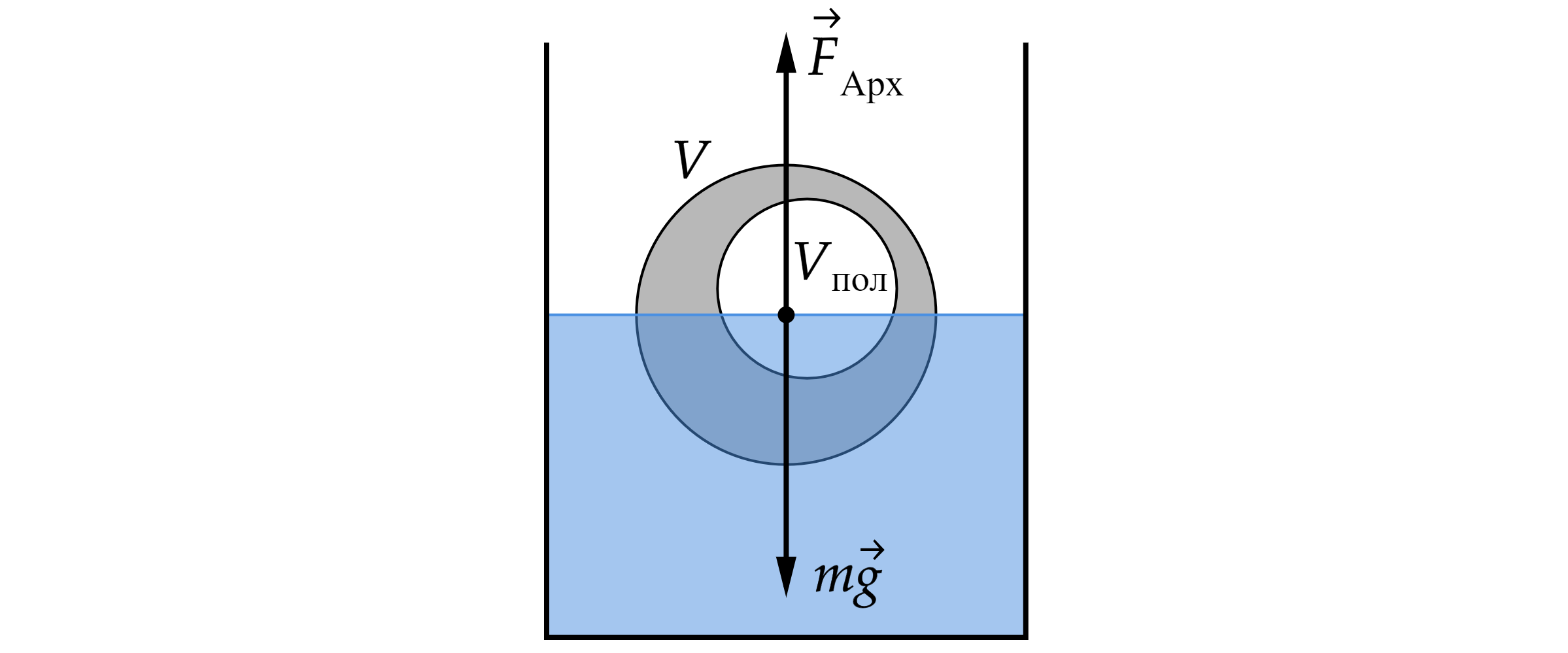
Сила Архимеда равна:

Fарх = ρgVп = ρg⋅0,54V,

где $ρ$ – плотность воды, $Vп$ – объём погружённого тела, $V$ – объём тела.
Так как тело плавает в воде, то выполнено равенство:

Fарх =mg = ρg⋅0,54V

Масса тела из алюминия равна

m = ρa⋅(V − Vпол)

где $ρa = 2700$ кг/м $3$ – плотность алюминия; $Vпол$ – объем воздушной полости. Подставляя данное выражение в первую формулу, имеем:

0,54ρgV = ρag(V − Vпол) ⇒ Vпол = V − V 0,54ρ-= 0,032 м3 ρa

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула силы тяжести, формула силы Архимеда, условие плавание тела (равенство силы Архимеда и силы тяжести))

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 9#41558

Металлический шарик, будучи полностью погружённым в воду, весит 3,9 Н, а в спирт – 4,0 Н. Чему равна средняя плотность шара?

Источники: Камзеева 2024

Показать ответ и решение

Пусть сила Архимеда, действующая на шарик равна $FA1$ и $FA2$ в первом и во втором случае соответственно, $m$ – масса шарика. При этом они равны:

FA1 = ρ1gV

FA2 =ρ2gV,

где $ρ1$ и $ρ2$ – плотности воды и спирта, $V$ – объём шарика.
Запишем второй закон Ньютона:

mg = ρ1gV +P1

mg = ρ2gV + P2,

где $P1$ и $P2$ – вес тела в первом и во втором случае. Тогда

-P2-− P1 ---------4 Н-−-3,9-Н-------- −5 3 ρ1gV +P1 = ρ2gV + P2 ⇒ V = g(ρ1− ρ2) = 10 Н/ кг(1000 кг/м3− 800 кг/м3) = 5⋅10 м

А искомая плотность:

3 −5 3 ρ= m-= ρ1gV-+-P1= 1000 кг/м-⋅10⋅-Н/кг5⋅1−05-м3--+3,9-Н =8800 кг/м3 V gV 10 Н/кг⋅5 ⋅10 м

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула силы Архимеда, второй закон Ньютона)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 10#50510

В вертикальные сообщающиеся сосуды поверх ртути (3) налиты различные жидкости. В один сосуд — столбик воды (1), а в другой — столбик спирта (2) высотой 25 см (см. рисунок). Определите высоту столбика воды, если разность уровней ртути в сосудах равна 5 см.

$PIC$

Источники: Камзеева 2024

Показать ответ и решение

Давление столба жидкости равно

p= ρgh,

где $ρ$ – плотность жидкости, $h$ – высота столба жидкости.
В сообщающихся сосудах жидкость устанавливается таким образом, чтобы в любой горизонтальной плоскости давление внутри жидкости оставалось неизменным. То есть выполняется условие:

ρ1h1 = ρ2h2,

где $ρ1$ и $h1$ – плотность и высота левого столбика, $ρ2$ и $h2$ – плотность и высота правого столбика.
В данном случае имеем следующее равенство:

ρвghв = ρсghс+ρртghрт

где $ρв = 1000$ кг/м $3$ –плотность воды; $ρс = 800$ кг/м $3$ – плотность спирта; $ρрт = 13600$ кг/м $3$ . Отсюда находим высоту уровня воды:

h в = ρсhс+-ρртhрт= 0,88 м ρв

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула давления столба жидкости, записано равенство давлений на одном уровне однородной жидкости)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 11#40853

На столе стоит сплошной медный куб. Какова масса куба, если оказывает на стол давление 8 кПа?

Показать ответ и решение

Давление равно:

F P = S,

где $F$ – приложенная сила, $S$ – площадь.
В нашем случае приложенная сила равна силе тяжести:

F = mg,

где $m$ – масса куба.
Масса равна:

m = ρV =ρSh,

где $ρ$ – плотность меди, $h$ – высота куба (в данном случае сторона куба).
Тогда

P = ρShg =ρgh. S

Отсюда:

h= -P = -----8000 Па-----≈ 0,09 м ρg 8900 кг/м3⋅10 Н/ кг

Объем куба:

V = h3 =0,093 м3

Тогда масса

m =ρV = 8900 кг/м3⋅0,093 м3 = 6,5 кг

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула связи давления и силы, формула силы тяжести, формула массы, формула давления, формула объёма)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 12#41029

Два сообщающихся сосуда с различными поперечными сечениями наполнены водой. Площадь поперечного сечения у узкого сосуда в 100 раз меньше, чем у широкого. На поршень $A$ поставили гирю весом 10 Н. Какой груз надо положить на поршень $B,$ чтобы оба груза находились в равновесии?

$PIC$

Показать ответ и решение

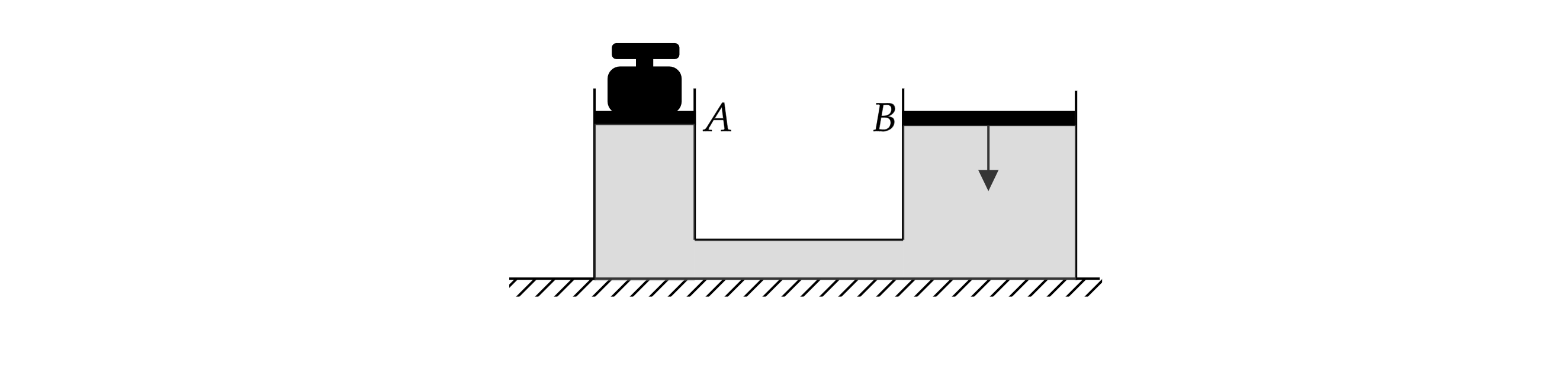
Для того, чтобы поршни находились в равновесии, необходимо, чтобы давления, оказываемые грузами были равны:

FA PA = SA-

PB = FB, SB

где $F A$ и $F = m g B B$ – силы тяжести грузов над поршнем $A$ и над поршнем $B$ соответственно, $S A$ и $S B$ – площади поршней, $mB$ – масса груза.
Тогда

F m g F ⋅S PA = PB ⇔ SA-= -SB-⇒ mB = -AgS--B. A B A

По условию $SB = 100SA$ , тогда

mB = FA-⋅100SA = 100FA-= 10-Н-⋅100 = 100 кг gSA g 10 Н/ кг

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула формула связи силы и давления, сказано про равенство давлений поршней, формула силы тяжести)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 13#41030

Поршень гидравлического пресса площадью 180 см² действует силой 18 кН. Площадь малого поршня 4 см². С какой силой действует меньший поршень на масло в прессе?

Показать ответ и решение

Для того, чтобы поршни находились в равновесии, необходимо, чтобы давления, оказываемые грузами были равны:

F1 P1 = S1

P2 = F2, S2

где $F 1$ и $F 2$ – силы, действующие на малый и большой поршни соответственно, $S 1$ и $S 2$ – площади малого и большого поршней соответственно
Тогда

F F S 4см2 P1 = P1 ⇔ S1 = S2⇒ F1 = F2S1 = 18000 Н18см2 = 400 Н 1 2 2

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула формула связи силы и давления, сказано про равенство давлений поршней)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 14#40852

Штормовой ветер силой 10 баллов создает давление на преграду около 100 Па. Определите силу давления на стену дома высотой 5 м и длиной 10 м, если ветер дует перпендикулярно поверхности дома?

Показать ответ и решение

Давление равно:

F P = S,

где $F$ – приложенная сила, $S$ – площадь.
Площадь стены:

S = ab,

где $a$ – высота, $b$ – длина.
То есть в нашем случае

F = PS =P ab= 100 Па ⋅5 м ⋅10 м =5000 Н

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула связи давления и силы, формула площади)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3