Тема Росатом

Параметры на Росатоме

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела росатом

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#83309

Область $G$ на плоскости, ограниченная двумя параболами $y =− 2x2 +3x$ и $y = x2+ px +q,$ имеет площадь 32. Вертикальная прямая $x =1$ разбивает её на две равновеликие части. Найти $p$ и $q$ .

Источники: Росатом - 2024, региональный вариант, 11.4 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Площади, графики, да тут всё намекает на определённый интеграл, а чтобы его найти надо посмотреть на модуль разности графиков, именно модуль, потому что площадь должна быть не отрицательной!

Подсказка 2

Нам сказано, что прямая x = 1 разбивает график на 2 равновеликие части, а парабола сама по себе фигура довольно симметричная, не можем ли мы что-то сказать про точку x = 1 для параболы?

Подсказка 3

Верно, это абсцисса вершины параболы, а мы умеем находить её через коэффициенты параболы, остаётся только посчитать определённый интеграл и получить условие на q, и задача будет уничтожена!

Показать ответ и решение

Обозначим данные параболы $y(x)= −2x2+3x 1$ и $y (x)= x2+ px+ q, 2$ пусть они пересекаются в точках с абсциссами $x1 < x2.$

Ограниченная ими площадь (над одним графиком и под другим) равна модулю разности площадей под графиками на отрезке $[x1,x2].$ А это по формуле Ньютона-Лейбница считается как

||∫ x2 ∫ x2 || ||∫ x2( 2 ) || || x1 y1(x)dx− x1 y2(x)dx||= ||x1 3x + (p − 3)x+ qdx||

Заметим, что полученный интеграл равен площади под графиком параболы $3x2+(p− 3)x+ q$ на отрезке $[x1,x2]$ . По условию прямая $x =1$ делит эту площадь на две равновеликие. Значит, $x= 1$ — абсцисса вершины этой параболы. С одной стороны, она равна $3−6p,$ а с другой стороны, $x1+2x2= 1.$ Тогда находим

3−-p =1 =⇒ p= −3 6

Теперь запишем данное в условии значение площади и получим уравнение на оставшийся параметр:

| | 32= ||∫ x2(3x2− 6x+ q)dx||=||(x3− x3− 3(x2 − x2)+q(x − x))||= |x1 | 2 1 2 1 2 1

| | | | = |(x2− x1)(x21 +x22+ x1x2 − 3x1− 3x2 +q)|=|(x2 − x1)((x1+x2)2− x1x2− 3(x1+ x2)+q)|=

|| 2q|| |||∘---4q 2q||| (∘ ---q)3 = ||(x2− x1)(−2+ 3-)||= || 4− -3 (2− 3-)||= 4 1− 3

(∘---q)3 8= 1 −3

q 4= 1− 3

q = −9

Ответ:

$p =−3,q = −9$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#76643

Найти все числа $C$ , для которых неравенство $|αsin x+β cos2x|≤C$ выполняется при всех $x$ и любых $(α;β)$ таких, что $2 2 α + β ≤ 4.$

Источники: Росатом-2022, московский вариант, 11.2 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Функции синус и косинус ограничены отрезком [-1;1]. Значит, можно оценить левую часть, избавившись от этих функций.

Подсказка 2

Найдите максимальное значение левой части при фиксированных коэффициентах и покажите, что оно достигается.

Подсказка 3

Используя второе условие, можно нарисовать получившиеся ограничения на C. Из рисунка будет понятно, какие значения подходят под ответ.

Показать ответ и решение

$f(x)= |αsin x+β cos2x|≤|α||sinx|+ |β||cos2x|≤ |α|+ |β|.$ Покажем, что значение $|α|+ |β|$ всегда достижимо для функции $f(x)$ при любых $(α;β):$

1. Если $α$ и $β$ одного знака, то $(3π) f 2 = |− α − β|= |α|+ |β|;$

2. Если $α$ и $β$ разных знаков, то $(π) f 2 =|α− β|=|α|+|β|$

Таким образом, при фиксированных $(α;β)$ максимальное значение $f(x)$ равно $|α|+|β|.$ В круге $2 2 α +β ≤4$ величина $|α|+ |β|$ принимает наибольшее значение $√- 2 2.$

$PIC$

Итак, при любых $(α;β)$ в круге $α2 +β2 ≤4$ и при любых $x$ справедливо неравенство $f(x)= |αsin x+β cos2x|≤2√2,$ так что любое $C < 2√2$ не удовлетворяет условию задачи, а $C ≥2√2$ искомое.

Ответ:

$C ≥ 2√2$

Ошибка.
Попробуйте повторить позже

Задача 3#48861

При каких $a$ уравнение $arcsin(cosx)=cos(arcsin(x− a))$ имеет единственное решение?

Источники: Росатом - 2021, 11.5, комплект 1 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Внимательно посмотрим на левую часть. С аркфункциями работать не хочется, поэтому нужно от них избавиться. Нам намного удобнее работать с выражением arccos(cos(x)). Попробуйте привести всё к нему в левой части.

Подсказка 2

Отлично! Левая часть равна π/2 - arccos(cos(x)). Теперь взглянем на правую часть. Тут также хочется избавиться от тригонометрических функций. Обозначьте arcsin(x - a) как за угол α и воспользуйтесь тем, что sin(α) = x - a.

Подсказка 3

Так, теперь мы получили, что левая часть равна √(1 - (x-a)^2). Попробуем изобразить графики полученных функций.(Заметьте, что левую часть можно рассматривать только на отрезке [-π;π], ведь у неё период 2π).

Подсказка 4

Нам нужно только одно решение. То есть можно смотреть только на a от -π до π, а потом записать ответ с периодом 2π. Теперь всего лишь осталось посмотреть, как наша полуокружность движется в зависимости от a, и найти точки, где одно пересечение.

Показать ответ и решение

Изобразим график $y = arcsincosx$ на $[−π,π]$ . Сама функция имеет период $2π$ , поэтому на остальной прямой график будет повторяться

$PIC$

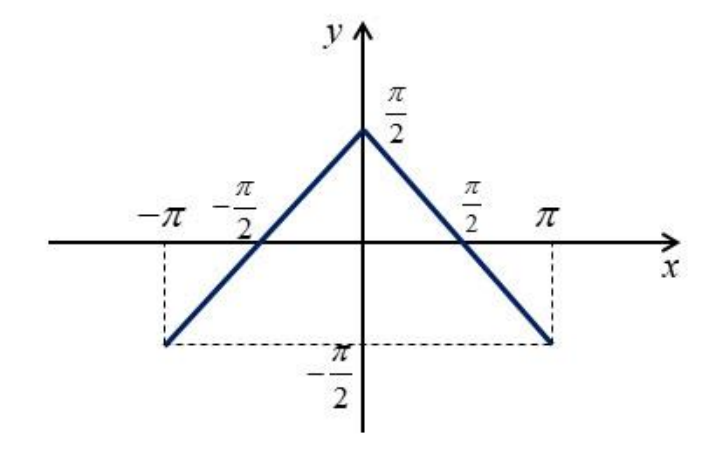
Теперь посмотрим на график правой части $∘ --------2 y = cosarcsin(x− a)= 1− (x− a)$ , который будет полуокружностью

$PIC$

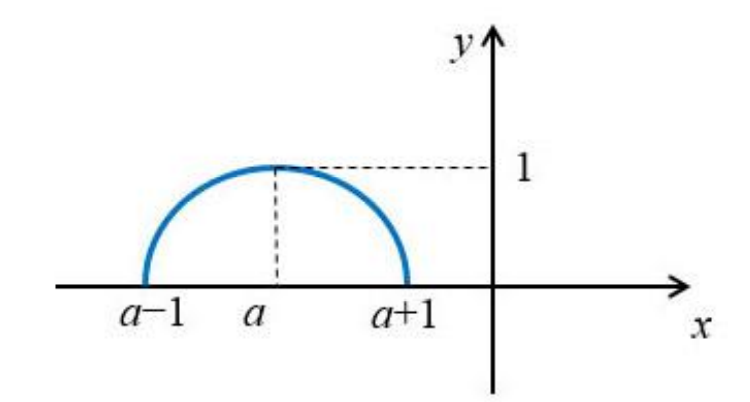
Например, графики будут расположены так при $a0 =− π$

$PIC$

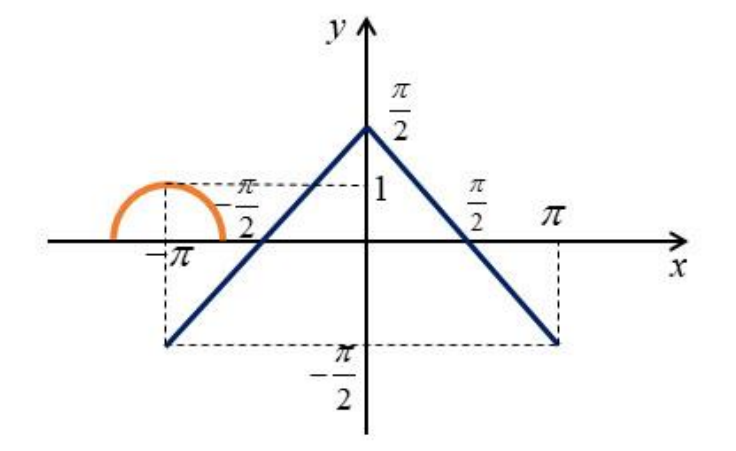
С ростом параметра $a$ оранжевый график перемещается вправо. Достаточно рассмотреть значения $a ∈[−π,π]$ , поскольку оранжевый график может пересекать не более одного “уголка” синего графика (помним про периодичность). Остаётся найти те значения параметра, при которых изменяется количество общих точек на $[−π,π]$ .

Первое такое значение будет в момент первого пересечения при движении оранжевого графика вправо

$PIC$

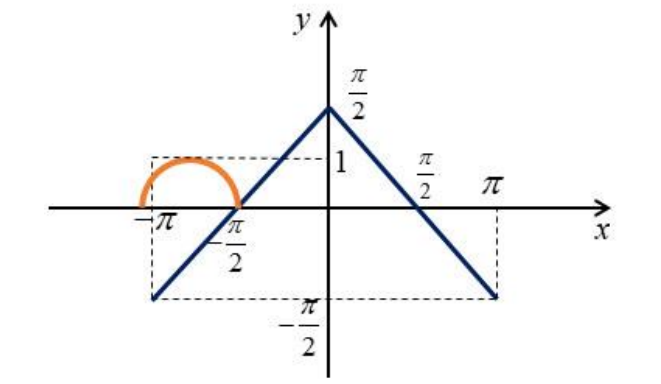
Заметим, что правая точка оранжевого графика соответствует $x= a+ 1$ , откуда

a+ 1= − π ⇐⇒ a1 =− π − 1 2 2

При дальнейшем движении решение будет только одно вплоть до положения

$PIC$

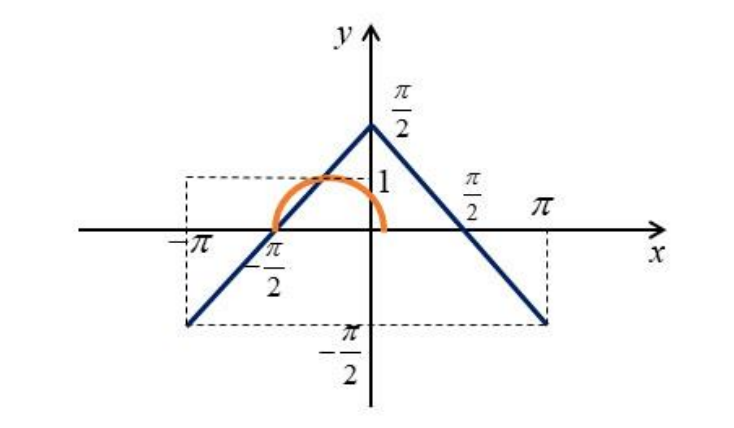
когда решений становится два. Левая точка оранжевого графика соответствует $x= a− 1$ , откуда

π π a− 1= −2 ⇐⇒ a2 =− 2 +1

Дальше решения будет два вплоть до положения, когда произойдёт касание

$PIC$

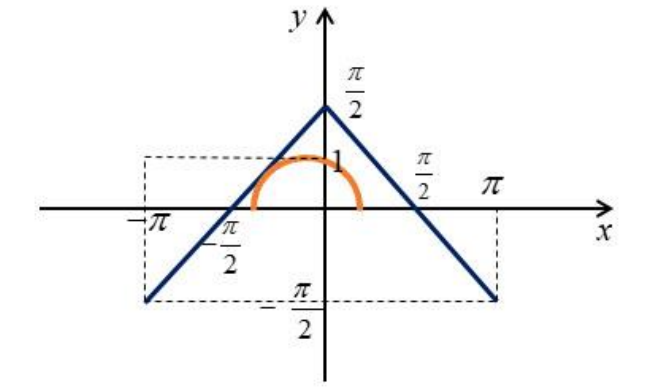
Поскольку касательная имеет коэффициент наклона $− 1$ , то на полуокружности это точка $1 1 (a− √2,√2)$ (учитывая смещение на $a$ из центра координат). При этом точка касания лежит на прямой $π y =x + 2$ (левая часть уголка), откуда

1 1 π π √- √2-= a− √2 + 2 ⇐ ⇒ a3 =− 2 + 2

Далее решений не будет вплоть до касания с противоположной стороны уголка в симметричной точке $a4 =− a3 = π2 − √2$ , где решение будет одно. Далее вплоть до $a5 = −a2 = π2 − 1$ решений два. Потом от неё до $a6 = π2 + 1$ решение единственное, а после до $a7 = π$ решений нет.

В итоге для единственности подойдут

a ∈[a1,a2)∪(a5,a6]∪{a3,a4}

Остаётся учесть период и написать ответ.

Ответ:

$[− π− 1+ 2πk,− π + 1+2πk)∪ (π − 1+2πk,π+ 1+ 2πk]∪{− π+ √2+ 2πk,π − √2-+ 2πk} , k∈ ℤ 2 2 2 2 2 2$

Ошибка.
Попробуйте повторить позже

Задача 4#80456

При каких значениях $a$ точка с координатами $(sina;sin3a)$ симметрична точке с координатами $(cosa;cos3a)$ относительно прямой с уравнением $x +y =0?$