Тема Межвед (на базе ведомственных образовательных организаций)

Планиметрия на Межведе

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела межвед (на базе ведомственных образовательных организаций)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#78851

На сторонах $BC$ и $CD$ квадрата $ABCD$ выбраны точки $E$ и $F$ таким образом, что угол $EAF$ равен $45∘.$ Длина стороны квадрата равна 1. Найдите периметр треугольника $CEF.$

Источники: Межвед - 2021, 11.3 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Что нам вообще дали в задаче? Сторону квадрата и угол в 45 градусов. Скудный набор. Но при этом чуть-чуть про периметр нам известно, что это часть у двух сторон квадрата. Какая возможная есть гипотеза про вероятный периметр треугольника?

Подсказка 2

Ага, у нас треугольник расположен в углу и, если "развернуть" его гипотенузу, то периметр будет равен сумме двух сторон квадрата. Теперь это надо доказать. Попробуем сделать такую хитрую штуку. Что произойдёт, если точку D сначала отразить относительно AF, а потом относительно AE? Куда перейдёт точка D?

Подсказка 3

Верно, точка D перейдёт в точку B! Это будет так, потому что композиция двух осевых симметрий относительно пересекающихся прямых — это поворот на удвоенный угол между прямыми. Получается, что у нас точки B и D при отражении относительно сторон являются одной точкой X на EF. Но чем на самом деле является точка X в треугольнике AEF?

Подсказка 4

Да, это основание высоты из точки A. Это вытекает из свойств симметрии. Осталось только аналогично понять равенство отрезков, и мы добились своей цели. Победа!

Показать ответ и решение

Первое решение.

Вспомним, что угол, под которым видна сторона треугольника из центра вневписанной окружности, равен $∘ α 90 − 2,$ где $α$ — угол, в который окружность вневписана.

Центр вневписанной окружности треугольника $CEF$ лежит на прямой $AC,$ т.к. биссектриса совпадает с диагональю квадрата $AC.$ Но при этом

∠ECF ∠EAF = 45∘ = 90∘−--2--,

то есть точка $A$ как раз является центром вневписанной окружности треугольника $CEF.$

$PIC$

Тогда точки $B$ и $D$ — точки касания вневписанной окружности с продолжениями сторон треугольника $CEF,$ а его периметр равен $BC + CD = 1+1 =2.$

Второе решение.

Если отразить точку $D$ относительно прямой $AF,$ а затем относительно прямой $AE,$ то она перейдет в точку $B.$ Действительно композиция двух осевых симметрий относительно пересекающихся прямых — это поворот на удвоенный угол между прямыми. То есть в нашем случае эти две симметрии эквивалентны повороту на угол $90∘$ относительно точки $A.$ Это означает, что образ точки $D$ при симметрии относительно $AF$ и образ точки $B$ при симметрии относительно $AE$ — это одна и та же точка; на рисунке она обозначена $K.$

$PIC$

Из точки $K$ отрезки $AE$ и $AF$ видны под углом $90∘$ (при симметрии сохраняются величины углов, поэтому например, углы $ABE$ и $AKE$ равны). Значит, точка $K$ — это основание перпендикуляра, опущенного из точки $A$ на прямую $EF.$ И, наконец, поскольку $BE = EK$ и $DF = FK$ (при симметрии длины отрезков сохраняются), видим, что периметр треугольника $CEF$ равен сумме длин сторон $BC$ и $CD$ квадрата.

Ответ:

$2$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#49012

В остроугольном треугольнике $ABC$ на стороне $AC$ выбрана точка $Q$ так, что $AQ :QC = 1:2.$ Из точки $Q$ опущены перпендикуляры $QM$ и $QK$ на стороны $AB$ и $BC$ соответственно. При этом $BM :MA = 4:1,BK =KC$ . Найдите $MK :AC$ .

Подсказки к задаче

Подсказка 1

Сначала стоит обратить внимание на QK, ведь это и медиана, и высота в △BQC. Делаем вывод про △BQC, а дальше, конечно, надо бы ввести какие-нибудь удобные обозначения для отношений на сторонах AB и AC!

Подсказка 2

Например, положим AQ = a и AM = b. Вообще, как мы собираемся считать тогда отношение MK:AC? Кажется, что мы хотим выразить MK и AC через какую-то одну переменную, тогда она при делении сократится. Значит, надо найти связь между a и b! Что из условия ещё остаётся неиспользованным?

Подсказка 3

Конечно же, перпендикулярность QM и AB! Попробуйте использовать образовавшиеся прямоугольные треугольники, чтобы найти эту самую связь между a и b. Может, это ещё натолкнёт нас на какой-нибудь крутой факт про BQ...

Подсказка 4

Действительно, проведя расчёты, получим, что BQ ⊥ AC. Теперь снова обратим внимание на △BQC. Помимо того, что он равнобедренный, теперь мы ещё знаем, что он прямоугольный, значит, углы при гипотенузе хорошие! Только вот как это можно использовать? Поскольку сторона AC выражается через a, то мы хотим выразить MK тоже через a. Может быть, теорема косинусов? Там как раз можно будет использовать найденный хороший угол! Только надо сначала сформировать подходящий треугольник.

Подсказка 5

А именно, проведём прямую, параллельную AC, через точку M, тогда образуется треугольник, высеченный этой прямой и MK. Осталось в нём найти стороны и использовать теорему косинусов!

Показать ответ и решение

$PIC$

Раз $QK$ и медиана, и высота в треугольнике $BQC$ , то он равнобедренный, и значит, $QC = QB$ . Пусть $AQ = a$ и $AM = b$ . Тогда $MB =4b$ и $BQ = QC =2a$ . Так как $MQ ⊥ AB$ , то $BQ2 − AQ2 = 3a2 = BM2 − AM2 = 15b2$ . Значит, $√ - a = 5b$ . Тогда $AQ2 + QB2 = 5a2 = 25b2 = AB2$ . Значит, $QB ⊥ AC.$

$PIC$

Проведем через $M$ прямую параллельную $AC$ . Мы знаем, что $BQ =QC$ и $∘ ∠BQC = 90$ , поэтому $∘ ∠MDK = ∠ACK = 45$ и $√- BC = 2 2a$ и $√- BK = KC = 2a$ . Из параллельности $MD- BM- BD- AC = AB =BC$ , поэтому $4 12a MD = 5 ⋅3a= 5$ , $8√2a- BD = 5$ и $8√2a √- 3√2a KD = 5 − 2a= 5$ . Тогда по теореме косинусов

2 18a2 144a2 72a2 90a2 KM = -25--+ -25-− -25-= -25-

Тогда

3a√-- √-- KM--= -5-10 = -10 AC 3a 5

Ответ:

$√10-:5$

Ошибка.
Попробуйте повторить позже

Задача 3#49013

Про пятиугольник $ABCDE$ известно, что

0 0 AB = BC = CD = DE,∠B = 96 ,∠C = ∠D = 108 .

Найдите $∠E.$

Подсказки к задаче

Подсказка 1

У нас есть много равных отрезков, а значит, равнобедренных треугольников! Какие из них наиболее выгодно рассмотреть?

Подсказка 2

Часто в самых разных задачах по математике выгодно придерживаться некоторой симметрии. У нас точки C и D как бы равноправны, поэтому давайте рассмотрим равнобедренные треугольники EDC и BCD и посчитаем их углы.

Подсказка 3

Теперь можно продолжить считать разные углы на картинке, пока не заметим что-нибудь интересное. Посчитайте все углы треугольников AFD и BFC (F - точка пересечения EC и BD). Что вы замечаете?

Подсказка 4

Эти треугольники равнобедренные! А значит, у нас ещё больше равных отрезков и где-то на картинке скрывается равносторонний треугольник...

Подсказка 5

Треугольник ABF оказывается равносторонним, и это помогает нам добраться до угла E!

Показать ответ и решение

$PIC$

Давайте пересечем $CE$ и $BD$ в точке $F$ . $180∘−∠C- ∘ ∠BDC = ∠DBC = 2 =36$ из равнобедренности $DCB$ . Аналогично, $∘ ∠ECD =∠CED = 36$ . Тогда $∘ ∠BF C = 72$ и из этого следует, что $∘ ∠BCF = 72$ . Значит, $BF = BC$ . Аналогично, $EF = ED$ .

$PIC$

Теперь посчитаем $∘ ∠ABF =∠ABC − ∠DBC =60$ . Значит, $AF = AB =BF = EF$ . Отсюда следует, что $∘ ∠AF E =48$ , $∘ ∠AEF = 66$ , $∘ ∠E = ∠AEC + ∠CED = 102$ .

Ответ:

$102∘$

Ошибка.
Попробуйте повторить позже

Задача 4#78850

В трапеции, площадь которой равна 1, каждая сторона поделена на три равные части. Соответствующие точки соединены отрезками, как показано на рисунке. Найдите площадь заштрихованной фигуры, если известно, что нижнее основание трапеции в два раза больше верхнего.

$PIC$

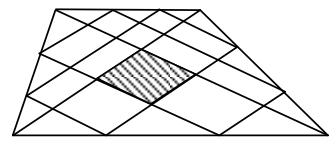
Источники: Межвед-2014, 11.8 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Обозначим нашу искомую площадь за S. Давайте сначала вспомним, что нам известно. Нам дали отношение оснований и площадь трапеции. О чём нам на самом деле говорит условие про отношение оснований? Как можно по другому его сформулировать?

Показать ответ и решение

Обозначим через $S = S ONRQ$ площадь заштрихованной фигуры.

$PIC$

По свойствам площадей треугольников с общим углом имеем:

SAOD-= 3⋅3= 9, SEQD 2⋅2 4

отсюда

4 5 SEQD = 9SAOD =⇒ SAOQE = SPNOD = 9SAOD

В то же время треугольник $ERP$ подобен треугольнику $AOD$ с коэффициентом подобия $1 3,$ значит

1 SERP = 9SAOD =⇒ SAOQE + SPNOD +SERP − S = SAOD

5 5 1 2 9SAOD+ 9SAOD − 9SAOD − S = SAOD =⇒ S = 9SAOD

При этом, $BC-+-AD- SABCD = 2 (h1+ h2),$ где $h1$ — высота треугольника $BOC$ и $h2$ — высота треугольника $AOD.$ Ясно, что $h1 = 1 2$ в силу подобия треугольников $BOC$ и $AOD$ с коэффициентом $1. 2$ Следовательно: