Тема Межвед (на базе ведомственных образовательных организаций)

Стереометрия на Межведе

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела межвед (на базе ведомственных образовательных организаций)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#68100

Из центра $O$ сферы радиуса $R$ проведены три луча, пересекающие сферу в точках $A,B$ и $C.$ Известно, что $∠AOB =∠AOC =∠BOC =60∘.$ Найдите площадь части сферы, ограниченной плоскостями $(AOB ),(AOC)$ и $(BOC).$

Источники: Межвед-2023, 11.8 (см. www.academy.fsb.ru)

Подсказки к задаче

Подсказка 1

Рассмотрите сначала две различные плоскости, проходящие через центр сферы. Пусть угол между этими плоскостями равен φ. Плоскости пересекают сферу по большим окружностям. На их пересечении получается криволинейный треугольник. Выразите его площадь через радиус и угол!

Подсказка 2

Три плоскости (содержащие грани трехгранного угла) разбивают сферу на 8 криволинейных треугольников. Искомую площадь криволинейного треугольника ABC обозначим через S, а его углы (которые, очевидно, являются двугранными углами трехгранного угла OABC ) за φ, ψ, θ. Примените формулу для площади криволинейного треугольника с углами φ, ψ, θ.

Подсказка 3

Примените теорему косинусов для трехгранного угла!

Показать ответ и решение

В задаче речь идет о трехгранном угле с вершиной в центре сферы, высекающем на сфере криволинейный треугольник. Площадь этого треугольника требуется выразить через радиус сферы и данные в условии плоские углы трехгранного угла, которые будем обозначать $∠AOB =α,∠AOC = β,∠BOC = γ.$

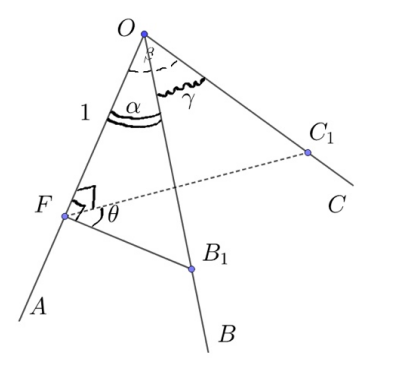
Рассмотрим сначала две различные плоскости, проходящие через центр сферы. Пусть угол между этими плоскостями равен $φ.$ Плоскости пересекают сферу по большим окружностям. Касательные к окружностям в их точке пересечения также образуют угол $φ.$ Площадь поверхности сферы равна $2 4πR .$ Площадь высекаемой плоскостями «дольки» (указанной на рисунке цветом) очевидно пропорциональна величине $φ$ и равна $2 φ- 2 4πR ⋅2π = 2R φ.$

$PIC$

Три плоскости (содержащие грани трехгранного угла) разбивают сферу на $8$ треугольников. Искомую площадь криволинейного треугольника $ABC$ обозначим через $S,$ а его углы (которые, очевидно, являются двугранными углами трехгранного угла $OABC )$ за $φ,ψ,𝜃.$ Площади криволинейных треугольников, примыкающих к сторонам треугольника $ABC,$ обозначим $Sφ,Sψ,S𝜃.$ С каждым из этих треугольников $ABC$ образует «дольку», поэтому $S +Sφ =2R2φ,S+ Sψ =2R2ψ,S+ S𝜃 = 2R2𝜃.$ Оставшиеся из $4$ -х нерассмотренных криволинейных треугольников симметричны $4$ -м рассмотренным относительно центра сферы. Значит, суммарная площадь рассматриваемых четырех треугольников равна половине площади сферы, то есть $S +Sφ +Sψ +S𝜃 =2πR2.$ Тогда сложим первые три уравнения и воспользуемся четвертым:

2S+ (S +Sφ +Sψ +S𝜃)= 2R2(φ + ψ+ 𝜃)

S = R2⋅(φ+ ψ+ 𝜃− π).

$PIC$

Из теоремы косинусов для трехгранного угла $OABC :$

1 φ= ψ = 𝜃= arccos3.

Отсюда получаем ответ.

$PIC$

Ответ:

$(3⋅arccos1− π)R2 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#79218

Основанием пирамиды $TABCD$ является трапеция $ABCD$ $(BC ∥AD).$ Расстояния от точек $A$ и $B$ до плоскости $TCD$ равны $r 1$ и $r2$ соответственно. Площадь треугольника $T CD$ равна $S.$ Найдите объем пирамиды $TABCD.$

Источники: Межвед-2020, 11.3 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

Давайте для начала поработаем с тем, что уже есть. Мы имеем r₁- расстояние от точки A до плоскости TCD, а также площадь треугольника △TCD. Чему же равен объем тетраэдра TACD?

Подсказка 2

Верно, r₁S/3. Из аналогичных рассуждений мы можем получить, что объем тетраэдра TBCD равен r₂S/3. Нам необходимо найти объем пирамиды TABCD. C учетом найденных объемов логично будет разбить его на две части: V(TABCD)=V(TABD)+V(TBCD). Какое равенство хочется доказать, чтобы завершить решение?

Подсказка 3

Конечно, V(TABD)=V(TACD). Это равенство равносильно равенству площадей треугольников △ABD и △ACD. Докажите это, учитывая, что у них есть общее основание AD, и завершите решение!

Показать ответ и решение

$PIC$

Объем пирамиды $TABCD$ равен сумме объемов пирамид $TBCD$ и $TABD$

VTABCD =VTBCD + VTABD

Причем $VTABD =VTACD$ , так как у этих пирамид общая высота(из вершины $T$ ), а также равны площади оснований: $SABD = SACD$ (у этих треугольников общее основание $BC$ и равные по длине высоты, проведенные из вершин $B$ и $C$ , поскольку $ABCD$ — трапеция по условию). Итак,