Тема . Аналитическая геометрия
.01 Векторы на плоскости. Операции над векторами.
Подтемы раздела
аналитическая геометрия
Решаем задачу:
Ошибка.
Попробуйте повторить позже
Задача 1#36857
Это нетрудная задача на повторение тех понятий, которыми мы будем пользоваться
при работе с векторами. Вспомните:
- 1.
- Что мы называем вектором? В чём отличие вектора от отрезка?
- 2.
- Что мы называем длиной вектора?
- 3.
- Какие векторы мы называем коллинеарными? А какие - сонаправленными? Противоположно направленными?
- 4.
- А какие векторы мы называем компланарными?
- 5.
- А какие векторы мы называем равными?
Показать ответ и решение
- 1.
- Вектор (на плоскости или в трёхмерном пространстве) - это упорядоченная
пара точек. В каком смысле упорядоченная? В том смысле, что мы
выбираем первую (скажем,
) и вторую (скажем, 
) точку и
запоминаем, в каком порядке мы их выбрали. Точку, выбранную первой,
в нашем случае 
мы будем называть началом вектора 
Точку же,
выбранную второй, в нашем случае 
мы, разумеется, будем называть
концом вектора 
Таким образом мы и задаём направление: как бы из
точки 
по направлению к точке 
Вот и получается, что, чтобы задать
направление вектора, нужно определиться, какая точка будет первой, а
какая - второй.
Разница с отрезком именно в этом и состоит. Когда мы определяем отрезок (на плоскости или в пространстве), нам неважно, в каком порядке мы брали точки, которые его определят.
Таким образом, с некоторой долей формализма, можно сказать, что отрезок - это неупорядоченная пара точек, а вектор - упорядоченная. И отсюда уже можно извлечь такое наблюдение: любой отрезок можно превратить в вектор, просто указав, какая точка у него первая, а какая - вторая, то есть указав, что считать началом этого отрезка, а что - концом.
Замечание: в некотором смысле школьная запись отрезка![[a;b]](/api/latex-service/v1/GetSession/71042/index-17cccfe9d4ffd49a505092c9b9d4deab.svg)
-
это скорее запись вектора, потому что здесь мы понимаем, что 
- это начало отрезка, 
- его конец. Но в аналитической
геометрии мы отойдём от такой традиции записи.
А векторы, в свою очередь, мы будем записывать вот так:
где
стрелочка означает, что это не отрезок, а именно вектор; первая
буква 
- это начало вектора; вторая буква 
- конец
вектора.
- 2.
- Под длиной вектора
как и всегда, будет пониматься длина отрезка,
соединяющего точки 
и 
Немного забегая вперёд, можно сказать, что, когда мы введём систему координат, допустим, на плоскости, то длина
будет считаться
по теореме Пифагора по формуле 
где
- координаты точек 
и 
соответственно:
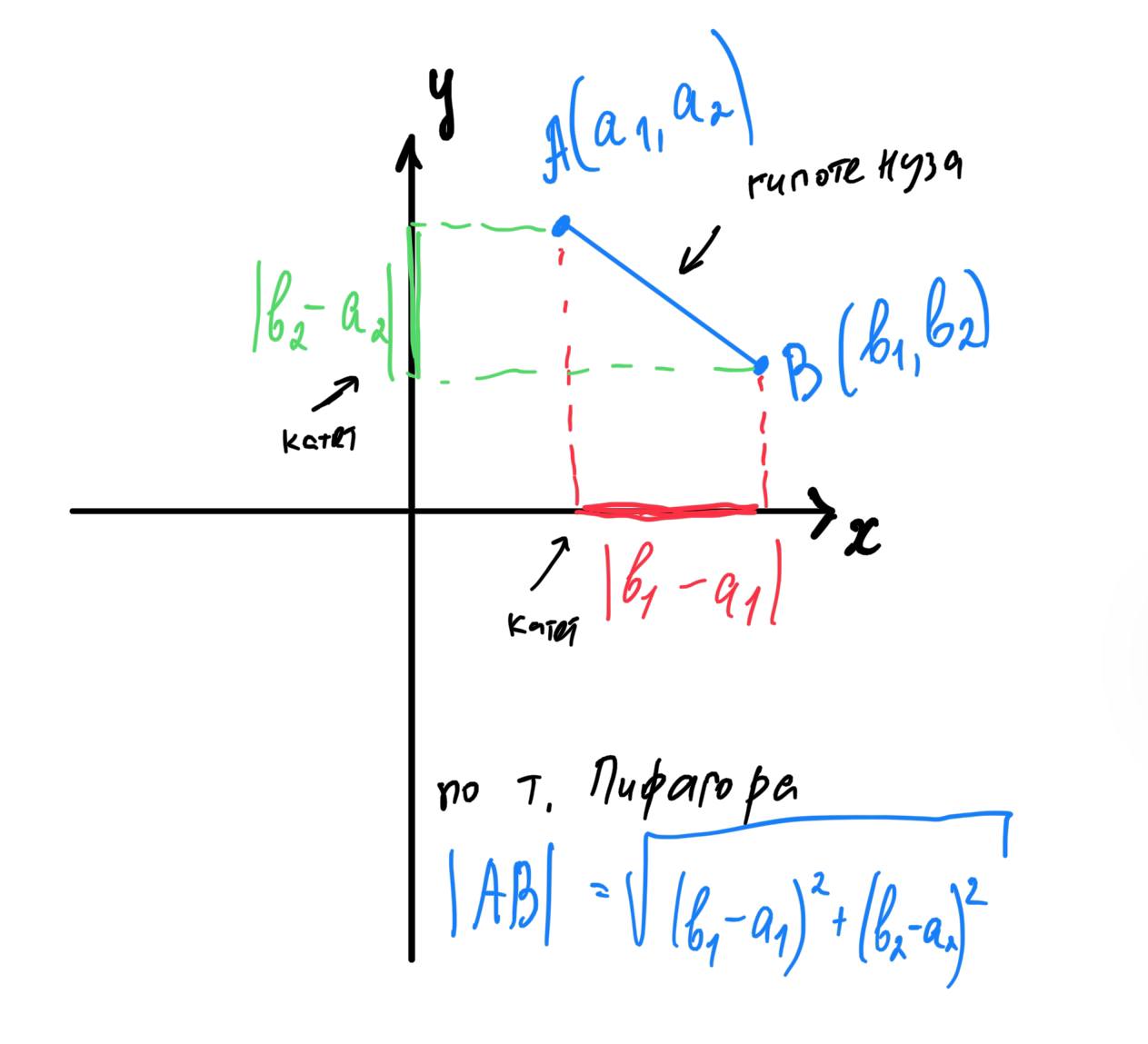
- 3.
- Коллинеарными мы называем вектора, лежащие на параллельных прямых (т.е. в
некоторым смысле и сами эти вектора можно назвать "параллельными"
но мы
так делать не будем. Для этого есть отдельный термин: коллинеарные вектора.)
Соответственно, существует два различных случая, каким образом два вектора
и 
могут быть коллинеарны. А именно: они могут быть либо
сонаправленными (обозначение: 
), либо противоположно
направленными (обозначение: 
).
- 4.
- Понятие компланарности вводится только для векторов в трёхмерном
пространстве. А именно, три вектора
называются
компланарными, если существует плоскость 
которой они все параллельны.
То есть, короче говоря, эти три вектора не задают никакого "объёма"
а,
будучи приведёнными к одному началу, будут лежать в одной плоскости.
(Внимание: для того, чтобы векторы
были компланарными,
вообще говоря, НЕ НЕОБХОДИМО, чтобы они изначально лежали в одной
плоскости. Попробуйте придумать такой пример.)
- 5.
- Чтобы вектор
мы назвали равным вектору 
необходимо, чтобы было
выполнено 3 условия:
a)
и 
должны быть коллинеарны.
b)
и 
должны быть одинаково направлены.
c)
и 
должны быть равны по длине.
На рисунке приведён пример равных, но не совпадающих векторов: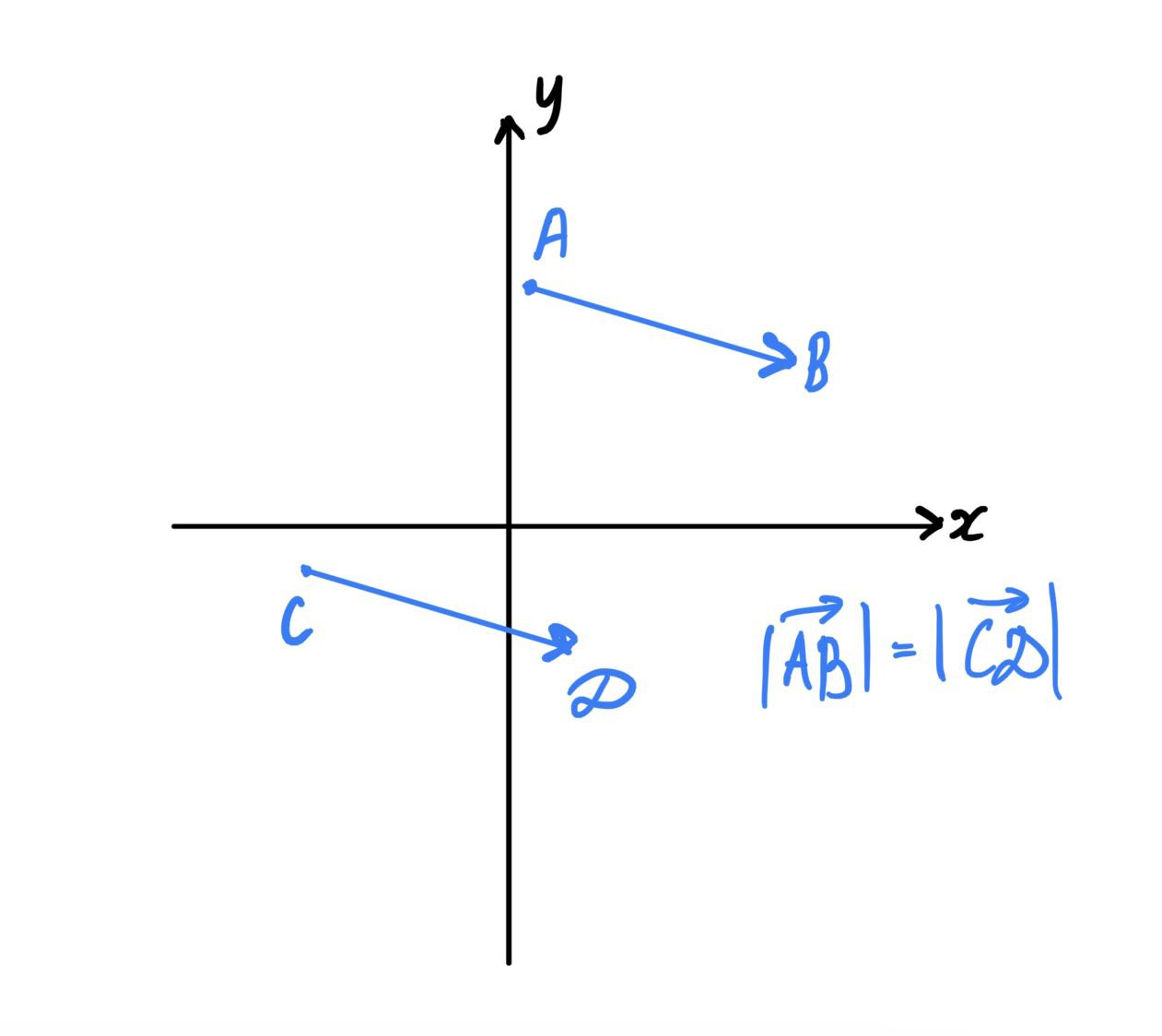
Ответ:
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
