Тема 4. Введение в теорию вероятностей

4.04 Сумма вероятностей совместных событий

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела введение в теорию вероятностей

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#1314

Вероятность того, что на тестировании по истории учащийся Т. решит больше 10 задач, равна 0,75. Вероятность того, что Т. верно решит больше 9 задач, равна 0,8. Найдите вероятность того, что Т. верно решит ровно 10 задач.

Показать ответ и решение

Для наглядности нанесем данные из условия на прямую:

$PIC$

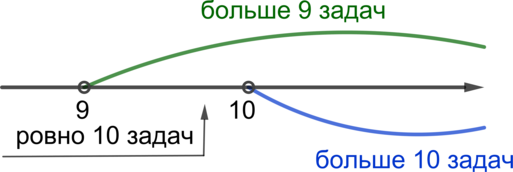
Тогда видим, что событие $A$ = { Т. решил больше 9 задач } состоит из объединения несовместных событий $B$ = { Т. решил больше 10 задач } и $C$ = { Т. решил ровно 10 задач }, а значит, вероятность события $A$ равна сумме вероятностей:

P(A) = P(B) + P(C)

Так как требуется найти вероятность события $C$ , то

P (C) = P (A)− P (B ) ⇔ P (C) = 0,8 − 0,75 = 0,05

Ответ: 0,05

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#1315

Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 16 пассажиров, равна 0,96. Вероятность того, что окажется меньше 10 пассажиров, равна 0,55. Найдите вероятность того, что число пассажиров будет от 10 до 15.

Показать ответ и решение

Для наглядности решения начертим рисунок:

$PIC$

Отсюда видим, что событие $A$ = { В автобусе окажется меньше 16 пассажиров } состоит из двух непересекающихся событий $B$ = { В автобусе окажется меньше 10 пассажиров } и $C$ = { В автобусе окажется от 10 до 15 пассажиров }, значит, для вероятностей можно записать:

P (A)= P(B)+ P (C )

Так как нам нужно найти вероятность события $C$ , то:

P(C)= P (A )− P(B)= 0,96− 0,55 =0,41

Ответ: 0,41

Ошибка.
Попробуйте повторить позже

Задача 3#2646

Вероятность того, что новый электрический чайник прослужит больше года, равна 0,9. Вероятность того, что он прослужит больше двух лет, равна 0,82. Найдите вероятность того, что чайник прослужит меньше двух лет, но больше года.

Показать ответ и решение

Рассмотрим следующий рисунок:

$PIC$

Из рисунка видно, что для нахождения вероятность того, что чайник прослужит больше года, но меньше двух лет, нужно из вероятности прослужить больше года вычесть вероятность прослужить больше двух лет.

Иными словами: событие $A$ = {чайник прослужит больше года} состоит из непересекающихся событий $B$ = {чайник прослужит большедвух лет} и $C$ = {чайник прослужит больше года, но меньше двух лет}, то есть $A = B ∪C.$

Значит, для вероятностей этих событий можно записать следующее:

P (A)= P(B)+ P (C )

Нам нужно найти вероятность события $C :$

P (C)= P(A)− P (B )

По условию $P(A) = 0,9,$ $P(B) = 0,82,$ тогда

P(C )= 0,9− 0,82 =0,08

Ответ: 0,08

Ошибка.
Попробуйте повторить позже

Задача 4#22941

Мама сварила малиновое варенье и разложила по банкам. Вероятность того, что варенье сохранится более трёх лет, равна 0,92. Вероятность того, что оно сохранится более четырёх лет — 0,84. Какова вероятность того, что варенье сохранится более трёх, но менее четырёх лет?

Показать ответ и решение

Если варенье сохранится более трёх лет, то оно испортится либо на четвертом году хранения, либо после четвертого года. Тогда события «варенье сохранится более четырёх лет» и «варенье сохранится более трёх, но менее четырёх лет», несовместны.

Значит, вероятность того, что варенье сохранится более трёх лет, равна сумме вероятностей событий «варенье сохранится более четырёх лет» и «варенье сохранится более трёх, но менее четырёх лет». Тогда вероятность того, что варенье сохранится более трёх, но менее четырёх лет, равна

p= 0,92 − 0,84= 0,08

Ответ: 0,08

Ошибка.
Попробуйте повторить позже

Задача 5#35

В аквариуме плавает 100 рыбок. Известно, что из них 17 золотых, 4 исполняют желания. При этом золотых рыбок, которые исполняют желания в аквариуме 3. Покупатель хочет приобрести золотую рыбку, которая исполняет желания (как в сказке). Найдите вероятность того, что выбранная наугад рыбка будет соответствовать хотя бы одному требованию покупателя.

Показать ответ и решение

Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления, тогда искомая вероятность равна

17- -4- -3- 18- 100 + 100 − 100 = 100 = 0,18

Ответ: 0,18

Ошибка.
Попробуйте повторить позже

Задача 6#36

Вероятность того, что маленький Миша заплачет, увидев в зоопарке медведя, составляет 0,3. Вероятность того, что маленькая Маша заплачет, увидев в зоопарке медведя, составляет 0,4. Вероятность того, что Миша и Маша вместе заплачут, увидев в зоопарке медведя, составляет 0,15. Какова вероятность того, что по крайней мере один из них заплачет, увидев в зоопарке медведя?

Показать ответ и решение

Событие «Маша или Миша заплачет» складывается из следующих элементарных событий.

Событие «Миша заплачет и Маша не заплачет» с вероятностью

0,3− 0,15

Событие «Миша не заплачет и Маша заплачет» с вероятностью

0,4− 0,15

Событие «Миша заплачет и Маша заплачет» с вероятностью 0,15.

Тогда искомая вероятность равна

p =(0,3 − 0,15)+(0,4− 0,15)+ 0,15= 0,55

Ответ: 0,55

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#37

Лампочка в левой комнате некоторого блока в общежитии перегорает в среднем 1 раз в 20 включений. Лампочка в правой комнате этого блока перегорает в среднем 1 раз в 50 включений. Вероятность того, что при одновременном включении лампочек обе перегорят, составляет 0,01. Какова вероятность того, что при одновременном включении ни одна из лампочек не перегорит?

Показать ответ и решение

Найдем вероятность того, что при одновременном включении хотя бы одна из этих лампочек перегорит.

Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления. Тогда вероятность того, что перегорит хотя бы одна лампочка, равна

1-+ -1− 0,01 = 0,05+ 0,02− 0,01= 0,06 20 50

Следовательно, вероятность того, что не перегорит ни одна лампочка, равна

1 − 0,06= 0,94

Ответ: 0,94

Ошибка.
Попробуйте повторить позже

Задача 8#636

Боря выступает на соревнованиях по спортивной гимнастике. Вероятность того, что он потянет ногу, равна $0,1$ , а вероятность того, что он вывихнет плечо, равна $0, 05$ . Обычно, даже получив повреждения, Боря не подает виду, так что вероятность потянуть ногу и вывихнуть плечо за одни соревнования составляет $0, 04$ . Какова вероятность того, что соревнования пройдут для Бори без таких травм?

Показать ответ и решение

Найдем вероятность того, что за соревнования Боря получит хотя бы одну из этих травм.

Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления, тогда вероятность получения Борей хотя бы одной из этих травм равна

0,1 + 0,05 − 0, 04 = 0,11.

Следовательно, вероятность не получить ни одной травмы равна $1 − 0,11 = 0,89$ .

Ответ: 0,89

Ошибка.
Попробуйте повторить позже

Задача 9#1377

В классе учится 20 человек, из которых 4 занимаются плаванием, а 5 занимаются шахматами. Известно, что и плаванием, и шахматами занимаются 2 ученика этого класса. Какова вероятность того, что выбранный наугад ученик этого класса занимается по крайней мере одним из этих видов спорта?

Показать ответ и решение

Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления.

Тогда искомая вероятность равна

4 5 2 7 20-+ 20 − 20 = 20 = 0,35

Ответ: 0,35

Ошибка.
Попробуйте повторить позже

Задача 10#1378

Среди десяти котят в коробке четверо мужского пола, у троих кончик хвоста белый. Известно, что ровно у 2 котят мужского пола кончик хвоста не белый. Таня выбирает себе одного котенка наугад. Какова вероятность того, что выбранный котенок будет мужского пола или с белым кончиком хвоста, или и то и другое?

Показать ответ и решение

Среди котят мужского пола в коробке у $4 − 2 = 2$ кончик хвоста белый. Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления, тогда искомая вероятность равна

4 3 2 10-+ 10-− 10-= 0, 5.

Ответ: 0,5

Ошибка.
Попробуйте повторить позже

Задача 11#1379

Вероятность того, что Артем получит пятерку по математике за ответ у доски, равна 0,97. Вероятность того, что Артем получит пятерку по русскому языку за ответ у доски, равна 0,9. Вероятность получить пятерку по обоим предметам оказалась равной 0,89. Какова вероятность того, что Артем не получит за ответы у доски по математике и русскому языку ни одной пятерки?

Показать ответ и решение

Найдем вероятность того, что за ответы у доски по математике и русскому языку Артем получит хотя бы одну пятерку.

Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления. Тогда вероятность получения Артемом хотя бы одной пятерки равна

0,97+ 0,9 − 0,89= 0,98

Следовательно, вероятность не получить ни одной пятерки равна

1− 0,98 = 0,02

Ответ: 0,02

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#1380

Маленький Алеша берет таблицу умножения и наугад выбирает себе пример, не подглядывая в ответ. Он умеет решать все примеры, в которых один из множителей равен 1, и все примеры, в которых один из множителей равен 5. Другие примеры он пока не освоил, поскольку ему всего 4 года. Какова вероятность того, что пример, который выберет Алеша, будет ему по силам, если таблица умножения обычная, то есть представляет из себя 100 примеров, начиная с $1 ×1,$ $1 ×2,$ ..., $2× 1,$ $2 ×2,$ ..., заканчивая $10× 10?$

Показать ответ и решение

В таблице умножения есть 19 примеров, где хотя бы один из множителей равен 1. Это 10 примеров вида $1× a$ и 9 примеров вида $b× 1,$ где $b⁄= 1.$

В таблице умножения есть 19 примеров, где хотя бы один из множителей равен 5. Это 10 примеров вида $5× a$ и 9 примеров вида $c× 5,$ где $c ⁄= 5.$ При этом есть два примера, в которых есть и 1 и 5. Это примеры $1 × 5$ и $5 ×1.$

Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления. Тогда вероятность того, что Алеше достанется пример, который он сможет решить, равна

19 19 2 100 + 100 − 100 = 0,36

Ответ: 0,36

Ошибка.
Попробуйте повторить позже

Задача 13#1930

Ваня бьет по мячу. Рядом стоит 10-этажный дом. Вероятность события «Ваня выбил окно на этаже, номер которого четный», равна 0,01. Вероятность события «Ваня выбил окно на этаже, номер которого делится на 3», равна 0,02. Вероятность того, что Ваня выбьет окно на 6-м этаже, равна 0,005. Какова вероятность того, что окна на четных этажах, как и окна на этажах с номерами, кратными 3, не пострадают?

Показать ответ и решение

Найдем вероятность того, что пострадает окно на четном этаже или пострадает окно на этаже, номер которого делится на 3.

Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления. Тогда вероятность того, что пострадает окно одного из оговоренных этажей, равна

0,01+ 0,02− 0,005= 0,025

Следовательно, вероятность того, что окна на четных этажах, как и окна на этажах с номерами, кратными 3, не пострадают, равна

1− 0,025 = 0,975

Ответ: 0,975

Ошибка.
Попробуйте повторить позже

Задача 14#19492

В торговом центре есть три одинаковых кофейных автомата. Вероятность того, что к концу дня в кофейном автомате закончится кофе, равна 0,3. Вероятность того, что к концу дня кофе закончится во всех трех кофейных автоматах, равна 0,05. Какова вероятность того, что к концу дня в торговом центре еще можно выпить кофе, но в первом автомате весь кофе закончился?

Показать ответ и решение

У каждого автомата есть два исхода: кофе в нем закончился (будем обозначать « $−$ »), и кофе в нем остался (будем обозначать « $+$ »). По условию вероятность того, что в первом автомате кофе закончился, равна 0,3. Заметим, что в событие «в первом автомате закончился кофе» входят следующие элементарные исходы:

1) во втором и в третьем автоматах тоже нет кофе $(−,−,−);$

2) во втором и третьем автоматах есть кофе $(− ,+, +);$

3) только во втором автомате остался кофе $(−,+,−);$

4) толька в третьем автомате остался кофе $(− ,−,+).$

Также по условию вероятность того, что во всех автоматах нет кофе $(−,−,−),$ равна 0,05.

Тогда вероятность того, что в первом автомате кофе закончился, а во втором или в третьем еще есть кофе, то есть вероятность события ${(− ,+,+);(− ,+, −);(−,− ,+ )},$ равна

0,3 − 0,05= 0,25

Ответ: 0,25

Ошибка.
Попробуйте повторить позже

Задача 15#31849

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Показать ответ и решение

В конце дня могло возникнуть четыре различных ситуации:

кофе остался в обоих автоматах $(++ )$ ;
кофе закончился только в первом автомате $(− +)$ ;
кофе закончился только во втором автомате $(+ −)$ ;
кофе закончился в обоих автоматах $(− −)$ .

Это и есть ни что иное, как наши четыре элементарных исхода. По условию для каждого автомата по отдельности вероятность того, что в нем закончится кофе, равна 0,3. Значит, событию «кофе закончилось в первом автомате», которое состоит из элементарных исходов ${(−+);(− −)}$ , соответствует вероятность 0,3. Событию «кофе закончится в обоих автоматах» соответствует ровно один элементарный исход $(− −)$ . Тогда

P((−+))= P ({(−+ );(−−)})− P((−−))= 0,3 − 0,12= 0,18

По аналогичным соображениям

P((+−))= P ({(+− );(−−)})− P((−−))= 0,3 − 0,12= 0,18

Теперь легко найти вероятность интересующего нас элементарного исхода «кофе остался в обоих автоматах $(++ )$ »:

P ({(++ );(−+ );(+− );(−−)})− P((−+))− P((+−))− P((−−))=

= 1 − 0,18− 0,18− 0,12 =0,52

Ответ: 0,52

Ошибка.
Попробуйте повторить позже

Задача 16#38826

При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,98. Вероятность того, что масса окажется больше 790 г, равна 0,83. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.

Показать ответ и решение

Вероятность того, что масса буханки окажется больше 810 г, равна $1 − 0,98= 0,02.$ Нам нужно найти вероятность того, что масса буханки окажется в диапазоне от 790 г до 810 г. Она равна разности вероятностей того, что масса буханки больше 790 г, и того, что масса буханки больше 810 г:

0,83 − 0,02= 0,81

Ответ: 0,81

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#41111

В небольшом магазине работают два продавца: Василий и Сергей. Каждый из них может быть занят работой с клиентом с вероятностью 0,4. При этом они могут быть заняты одновременно с вероятностью 0,3. Найдите вероятность того, что в случайно выбранный момент времени занят только Василий, а Сергей свободен.

Показать ответ и решение

Событие «Василий занят», вероятность которого равна 0,4, состоит из событий «Василий занят, а Сергей свободен» и «Василий и Сергей заняты», вероятность которого равна 0,3. Следовательно, вероятность события «Василий занят, а Сергей свободен» равна

p= 0,4− 0,3= 0,1

Ответ: 0,1

Ошибка.
Попробуйте повторить позже

Задача 18#72201

В роддоме измеряют вес новорожденных детей. Вероятность того, что вес окажется не меньше 3000 г, равна $0,87.$ Вероятность того, что вес окажется не больше 3600 г, равна $0,93.$ Найдите вероятность того, что вес случайно выбранного новорожденного окажется в пределах от 3000 до 3600 г.

Показать ответ и решение

Если вероятность того, что вес окажется не меньше 3000 г, равна $0,87,$ то логично, что вероятность того, что вес окажется меньше 3000 г, равна $1 − 0,87 = 0,13.$

События $A = {В ес меньш е 3000 г}$ и $B = {Вес не больш е 3600 г}$ имеют общие исходы, причем событие $B$ полностью содержит в себе событие $A,$ поэтому чтобы найти ответ к задаче следует из вероятности наступления $B$ вычесть вероятности наступления $A :$

P (B)− P (A) = 0,93− 0,13 = 0,8.

Ответ: 0,8

Ошибка.
Попробуйте повторить позже

Задача 19#74199

Вероятность того, что в автобусе едет меньше 10 человек, равна $0,29.$ Вероятность, что в автобусе едет не более 16 человек, равна $0,68.$ Найдите вероятность того, что в автобусе едет от 10 до 16 человек.

Показать ответ и решение

Пусть событие $A:$ в автобусе едет меньше 10 человек, $B :$ в автобусе едет от 10 до 16 человек. Тогда событие $A +B :$ в автобусе едет не более 16 человек. События несовместны, а значит можно использовать формулу

P(A + B)= P(A)+ P (B )

Тогда искомая вероятность равна

P(B) =P (A + B)− P (A )= 0,68− 0,29= 0,39

Ответ: 0,39

Ошибка.
Попробуйте повторить позже

Задача 20#83433

На тестировании по математике учащийся А. верно решит больше 4 задач с вероятностью 0,76. Вероятность того, что А. верно решит больше 3 задач, равна 0,89. Найдите вероятность того, что ученик верно решит ровно 4 задачи.

Источники: ЕГЭ 2024, досрочная волна

Показать ответ и решение

Вероятность того, ученик верно решит ровно 4 задачи, равна разности вероятностей того, что учащийся А. верно решит больше 4 задач, и того, что учащийся А. верно решит больше 3 задач.

$t034pp12 = = 00,8,796$

Тогда искомая вероятность равна

p = p1− p2 = 0,89− 0,76= 0,13.

Ответ: 0,13

Предыдущий раздел

Следующий раздел