Закл (финал) 11 класс
Ошибка.
Попробуйте повторить позже
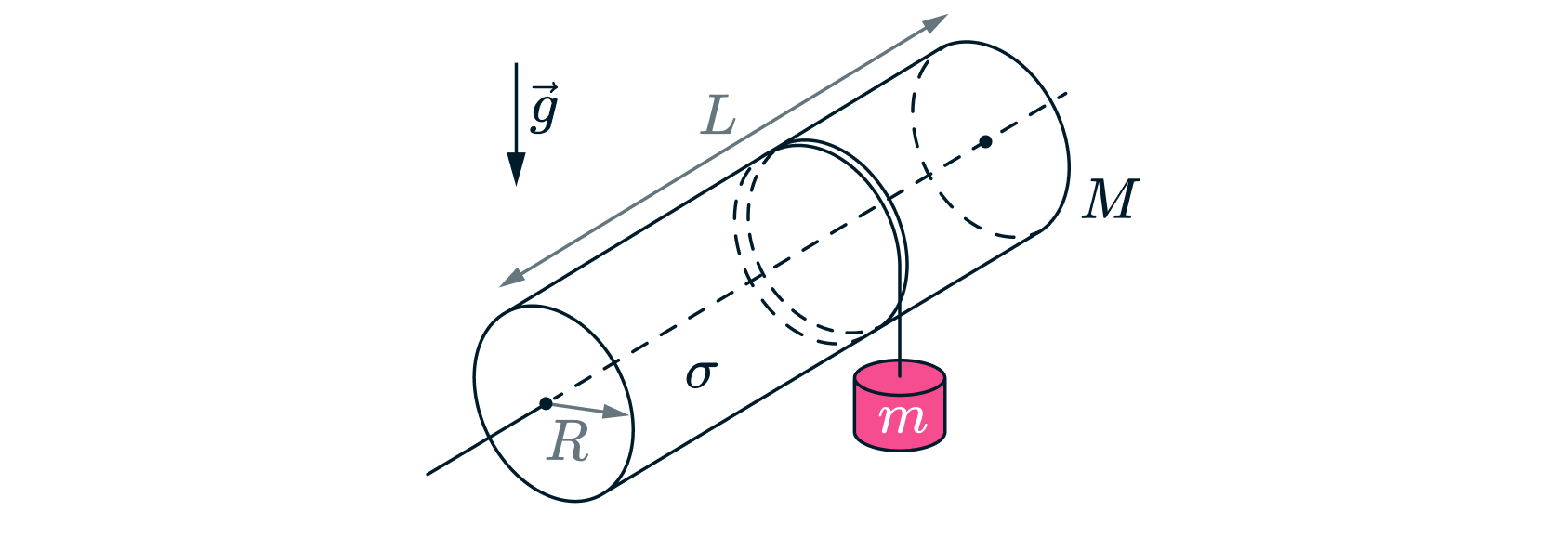
На длинном тонкостенном диэлектрическом цилиндре радиуса длины
и массы
размещён электрический
заряд одинаковой поверхностной плотностью
. Цилиндр может свободно (без трения) вращаться вокруг своей оси под
действием груза массы
подвешенного на невесомой нити, намотанной на цилиндр (рис.). Определите ускорение груза.
Магнитную постоянную
считать заданной.
(Всеросс., 2008, финал, 11)
Источники:
Как выразить индукцию магнитного поля, создаваемого вращающимися зарядами?
Проведем аналогию между вращающимся заряженным цилиндром и соленоидом с током, текущим по нему. В обоих случаях заряд движется по цилиндрической поверхности с круговой траекторией. Индукция магнитного поля в соленоиде B=мю0 N/l I0, где NI0 - полный ток, текущий по цилиндру. По определению силы тока NI0=dq/dt, где заряд, проходящий через поперечное сечение цилиндра dq=сигма vdt L. Таким образом можем получить, что индукция магнитного поля пропорциональна линейной скорости вращения цилиндра v.
Как выразить энергию магнитного поля?
Объемная плотность энергии магнитного поля w=B^2/2мю0, подставляя полученное выражение для индукции магнитного поля и домножая на объем цилиндра, можем получить, что энергия магнитного поля пропорциональна квадрату скорости вращения цилиндра.
Как связать движение груза и цилиндра?
Поскольку потерь энергии в системе нет можем записать закон сохранения энергии. Потенциальная энергия цилиндра постоянна, потенциальная энергия груза зависит от его координаты х по вертикальной оси. Груз и цилиндр обладают кинетической энергий, пропорциональной квадрату линейной скорости. Также энергия магнитного поля, создаваемого вращающимися зарядами на цилиндре, пропорциональная квадрату скорости. Запишем закон сохранения энергии и продифференцируем его с учетом того, что скорость груза v это производная его координаты x, взятая с обратным знаком. Сокращая на скорость, можем выразить производную скорости v, т.е. ускорение a груза.
1. Запишем величину модуля вектора магнитной индукции в центре цилиндра (пользуемся аналогией с соленоидом).
заметим, что - суммарный ток, проходящий через поперечное сечение при вращении цилиндра. Для этого тока
имеем:
тогда величина перепишется следующим образом:
Обратите внимание: чем быстрее происходит вращение цилиндра, тем больше величина модуля вектора магнитной
индукции
2. Запишем выражение для объемной плотности энергии магнитного поля цилиндра:
тогда несложно записать выражение для полной энергии магнитного поля цилиндра, с учетом выражения, полученного
ранее для .
Константа введена для упрощения решения.
3. Направим ось вдоль нити. Поскольку нить нерастяжима скорость вдоль нити одинакова, значит одинаковы
скорость груза и скорость вращения цилиндра. Кинетическая энергия вращения цилиндра:
где – момент инерции цилиндра,
– угловая скорость его вращения.
Момент инерции цилиндра:
Связь угловой скорости с линейной:
Итого для кинетической энергии цилиндра имеем:
Положим координату груза равной , координата цилиндра при этом остается постоянной и равной
. Запишем
закон сохранения энергии:
Продифференцируем:
Теперь достаточно заметить, что и переписать дифференциальное уравнение:
Решать его не придётся, нам достаточно лишь выразить для ответа на вопрос задачи. Делаем это и получаем
итоговый ответ:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




