Тема БИБН (Будущие исследователи - будущее науки)

Планиметрия на БИБНе

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела бибн (будущие исследователи - будущее науки)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#79609

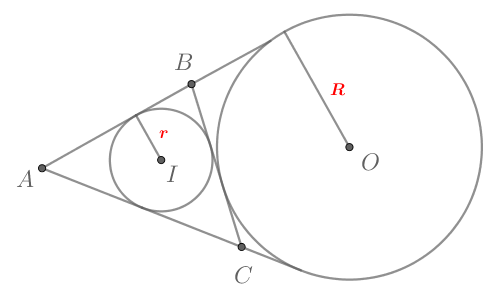
Дан треугольник $ABC$ , в который вписана окружность с центром $O$ . Пусть $M$ и $N$ — точки касания вписанной окружности со сторонами $AB$ и $AC$ . Известно, что $AO = 2⋅MN.$ Найдите $∠A.$

Источники: БИБН - 2024, 11.1 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1

У нас имеется отношение AO/MN=2. Мы все прекрасно помним, что отношение длин отрезков на окружности легко переносится на отношение синусов уголочков. Почему бы нам тогда не найти окружность, у которой есть хорды AO и MN...

Подсказка 2

Она легко находится- это окружность, построенная на AO как на диаметре. Тогда мы можем написать расширенную теорему синусов: MN/sin∠A=2R=AO. Тогда мы получаем, что sin∠A=MN/AO=1/2. Не забудьте, что синусы смежных уголков равны и найдите уголочек!

Показать ответ и решение

Пусть $∠A = 2α.$ Обозначим через точку $K$ пересечение $MN$ и $AO$ . Тогда, если радиус окружности равен $r$ , то из прямоугольного треугольника $MKO$

1 ∘ 2MN = MK =r⋅sin(90 − α)= r⋅cosα

$PIC$

Выразим $AO$ из прямоугольного треугольника $AMO$

AO = -r-- sinα

Подставляя в $AO = 2⋅MN$ , получаем

-r-- 4r⋅cosα= sinα

1 sin2α= 2

$∘ ∘ 2α = 150 или 30$ как угол треугольника.

Ответ:

$150∘ или 30∘$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#49716

Дан треугольник, у которого длины сторон — числа рациональные. Докажите, что рациональным числом является

а) отношение $R :r,$ где $R$ и $r$ — радиусы описанной и вписанной окружности;

б) значение $α β γ sin 2 ⋅sin 2 ⋅sin 2,$ где $α,$ $β,$ $γ$ — углы треугольника.

Источники: БИБН-2023, 11.3 (см. www.unn.ru)

Подсказки к задаче

Пункт а), подсказка 1

В условии сказано сразу про три стороны треугольника. Какие формулы сразу с величинами всех сторон есть в геометрии?

Пункт а), подсказка 2

Если в условие что-то говорится сразу про три стороны треугольника, то полезным будет воспользоваться формулами площади для треугольника: через стороны и радиус описанной, через полупериметр и радиус вписанной и формулой Герона.

Пункт а), подсказка 3

Правильно выразив и подставив величины из формул, можно найти отношение R/r.

Пункт б), подсказка 1

Полезным будет выразить гамма через альфа и бетта, пользуясь теоремой о сумме углов треугольника.

Пункт б), подсказка 2

Вместо гамма теперь в аргументе синуса стоит (180-альфа-бетта) Нужно попробовать свести все аргументы к сумме либо разности альфа и бетта.

Пункт б), подсказка 3

Аккуратно и правильно примените несколько тригонометрических формул из произведения в сумму.

Пункт б), подсказка 4

В конечном итоге мы получаем выражение которое зависит только от косинусов альфа, бетта и гамма. Рациональность данных величин нетрудно доказать, используя теорему косинусов.

Показать доказательство

Первое решение.

Введём длины сторон, как $a,b,c∈ ℚ,$ $S$ — площадь, $a+b+c- p = 2 ∈ ℚ$ — полупериметр. Далее воспользуемся формулами $abc ∘---------------- S =pr = 4R = p(p− a)(p− b)(p− c),$ откуда

R abcp abc r =-4S2-= 4(p-− a)(p-− b)(p−-c) ∈ℚ

Для углов известно $α+ β+ χ= π,$ зная это, распишем произведение

( ) ( ) sin αsin βsin χ-= 1 cos α−-β− cosα-+-β sin π−-α−-β= 1 cosα-− β-− cosα-+β cosα+-β= 2 2 2 2 2 2 2 2 2 2 2

= 1(cosα+ cosβ − cos(α +β)− 1)= 1(cosα+ cosβ +cosχ− 1) 4 4

Осталось воспользоваться теоремой косинусов. Например, для угла $χ$ имеем

2 2 2 c = a + b − 2abcosχ =⇒ cosχ ∈ℚ

То есть косинусы также рациональны, откуда следует рациональность произведения.

Второе решение.

а)

$PIC$

Мы знаем, что $S = pr,$ где $S$ — площадь треугольника, а $p$ — его полупериметр. С другой стороны, $S = abc, 4R$ где $a,$ $b,$ $c$ — стороны треугольника. Тогда

r= S, R = abc p 4S

Следовательно,

abc S- abc⋅p- R :r= 4S :p = 4S2

По формуле Герона

S2 = p(p− a)(p− b)(p− c)

Тогда

abc⋅p abc R:r= 4p(p− a)(p-− b)(p−-c) = 4(p-− a)(p−-b)(p−-c)

Заметим, что здесь каждый из множителей рационален, а следовательно и отношение рационально.

б) Запишем теорему синусов:

AB-- AC-- BC-- sinγ = sinβ = sinα =2R

Отсюда получаем

AB =2R sinγ, AC = 2Rsinβ, BC = 2R sinα

Пусть $I$ — точка пересечения биссектрис треугольника $ABC.$ Рассмотрим треугольник $BIC$ и запишем для него теорему синусов:

BC BI CI sin(90∘+-α)-= sinγ-= sinβ- 2 2 2

$PIC$

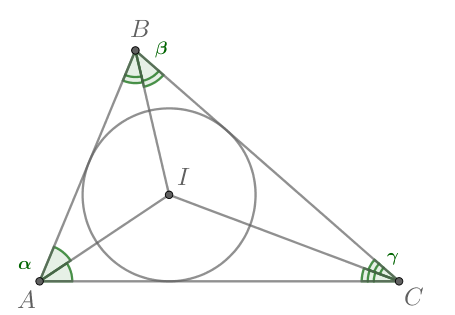
Подставим $BC = 2Rsinα,$ распишем синус двойного угла и синус суммы, получим

4R sinα cosα BI CI ---co2sα--2-= sinγ-= sin-β 2 2 2

Отсюда получаем

$pict$

Аналогично

β γ AI = 4R sin2 sin2

Заметим, что

$pict$

Таким образом,

α β γ r r sin2-⋅sin2 ⋅sin2 = 4R-sinβ-sinγ-⋅4Rsin-αsin-γ⋅ 2 2 2 2 ⋅----r-----= ---------r3--------- 4Rsin α2 sin β2 43R3sin2 α2 ⋅sin2 β2 ⋅sin2 γ2

Тогда

3 α 3 β 3 γ -r3- α- β γ -r- sin 2 ⋅sin 2 ⋅sin 2 = 43R3 ⇒ sin 2 ⋅sin 2 ⋅sin 2 = 4R

По предыдущему пункту $R:r$ рационально, значит и $r:4R$ рационально.

Ошибка.
Попробуйте повторить позже

Задача 3#68257

На стороне $BC$ треугольника $ABC$ взята точка $M$ такая, что $∠BAM =∠BCA$ . Докажите, что центр окружности, описанной около треугольника $ABC$ , лежит на прямой, проходящей через точку $B$ и перпендикулярной $AM$ .

Источники: БИБН-2021, 10.3 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1

Обозначим за O - центр нашей окружности. Пускай прямая BO пересекает прямую AM в точке T. Как нам доказать, что угол BTA прямой, если мы уже знаем что-то про уголок BAM...

Подсказка 2

Хочется понять, что ∠BAT + ∠ABT = 90°. Но мы уже знаем, что ∠ ABT = ∠ ABO, а ∠ BAT = ∠ BAM = ∠ BCA. Надо попробовать этим воспользоваться!

Подсказка 3

Если мы докажем, что ∠ ABO + ∠ BCA = 90°, то мы докажем, что ∠ BAT + ∠ ABT = 90°. Мы ещё вроде как не пользовались тем, что ∠ AOB = 2 * ∠ACB и OA=OB=R...

Подсказка 4

Т.к. △ AOB - равнобедренный с углом при вершине 2 * ∠ACB, то уголки ABO и BAO равны 90° - ∠ACB. Что мы и хотели выяснить?

Показать доказательство

На прямой, проходящей через точку $B$ и перпендикулярной прямой $AM$ , возьмем такую точку $N$ , что $AN = BN$ (она лежит на серединном перпендикуляре к $AB )$ . Тогда $∘ ∠NAB = ∠ABN = 90 − ∠MAB$ , поэтому

∘ ∘ ∠ANB =180 − 2∠NAB = 2(90 − ∠ABN )= 2∠MAB = 2∠ACB

$PIC$

Отсюда следует, что точка $C$ лежит на окружности, проходящей через $A$ и $B$ , с центром в точке $N$ . Действительно, для этой окружности $∠ANB$ — центральный, а $∠ACB$ -вписанный (если бы точка $C$ лежала вне этой окружности, то $∠ACB$ был бы меньше половины центрального, а если бы точка С была внутри окружности, то $∠ACB$ был бы больше половины центрального).

Ошибка.
Попробуйте повторить позже

Задача 4#69043

Дан равнобедренный треугольник $ABC$ с основанием $AC$ . Пусть $M$ — точка пересечения медиан. Докажите, что $∠BAM < 2∠MAC$ .

Источники: БИБН - 2021, 11.2 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1

Вспомните, как должны располагаться биссектриса и медиана, проведенные из острого угла прямоугольного треугольника? Что будет лежать выше?

Подсказка 2

Конечно, медиана будет пересекать катет выше биссектрисы! Что это говорит о углах, на которые медиана делит острый угол? Как же теперь использовать данный факт в нашей задаче?

Подсказка 3

Например, прямоугольный треугольник можно получить, если провести высоту ВК из вершины В, на ней же лежит и точка М. Вспомните, в каком отношение М делит ВК.

Подсказка 4

В отношении 2 к 1, считая от В. Тогда можно отметить Р — середину ВМ. Теперь есть две медианы АР и АМ в △ВАМ и △РАК соответственно, значит, можно применить выше упомянутое свойство (возможно, оно работает не только для прямоугольных треугольников, выясните)

Показать доказательство

Первое решение.

$PIC$

Вспомним следующую конструкцию: проведем две перпендикулярные прямые и на одной из них отметим точку, из которой отложим два равных угла, получив прямоугольный треугольник. Тогда $a <b$ где $a$ и $b$ — отрезки, на которые проведенная биссектриса делит сторону треугольника. Это следует из свойства биссектрисы: пусть $y$ — гипотенуза, $x$ — катет, тогда $ab = xy$ и так как $x< y,$ получаем $a< b.$ Также проведем медиану из отмеченной точки. Она будет пересекать катет выше биссектрисы в силу $a <b.$

$PIC$

По свойству точки пересечения медиан, $BM :MK = 2:1$ . Пусть $BM = 2x, MK = x$ . Отметим $P$ — середину $BM$ , тогда $BM =P M = x$ .

Проведем биссектрису угла $BAK$ . По сказанному ранее $∠MAK >∠P AM$ (биссектриса пересечет $BK$ в точке, которая находится ниже $M$ — середины $PM$ )

Треугольник $ABM$ — тупоугольный, поэтому $AB >AM$ так как $AB$ опирается на тупой угол. Проведем биссектрису угла $BAM$ . Она пересечет $BM$ ниже, чем точка $P$ — середина $BM.$ Поэтому $∠BAP < ∠P AM$

Итого получаем

∠MAK > ∠P AM > ∠BAP

То есть

{ ∠MAK > ∠P AM ∠MAK > ∠BAP

Складывая, получаем

2∠MAK > ∠PAM + ∠BAP

2∠MAC > ∠BAM

Второе решение.

$PIC$

Пусть $BK$ — медиана равнобедренного треугольника $ABC$ , проведенная к основанию $AC$ , тогда отрезок $BK$ перпендикулярен основанию $AC$ по свойству равнобедренного треугольника. По свойству точки пересечения медиан, $BK :MK = 3:1$ . Обозначим $∠MAK = α$ и $∠BAK = β$ . Тогда неравенство $∠BAM < 2∠MAC$ равносильно неравенству $β < 3α$ . Последнее неравенство очевидно в случае, когда $α≥ π6$ , так как $β < π2.$

Пусть теперь $α< π6$ . Из прямоугольного треугольников $ABK$ и $AMK$ имеем: $tgβ = BAKK-$ , $tgα = MAKK-$ , значит, $tgβ = 3tgα$ . Так как углы $β$ и $3α$ лежат в интервале $(0;π2)$ , то неравенство $β <3α$ равносильно неравенству $tgβ <tg3α$ , то есть $3tgα <tg3α$ .

Рассмотрим разность

tg3α − 3 tgα =(tg3α− tgα)− 2tgα=---sin2α-- − 2sinα-= 2sinα-− 2-sinα cos3α⋅cosα cosα cos3α cosα

Так как $0< α < π 6$ , то $0< cos3α <cosα$ и $sinα >0$ , и, значит,

(--1-- -1--) 2sinα cos3α − cosα > 0

следовательно, $tg3α− 3tgα> 0$ .

Ошибка.
Попробуйте повторить позже

Задача 5#68266

На стороне $AD$ выпуклого четырёхугольника $ABCD$ отмечена точка $O.$ Оказалось, что $AO =BO, CO =OD$ и $∠BOA = ∠COD.$ Пусть $E$ — точка пересечения диагоналей четырёхугольника. Докажите, что $EO$ — биссектриса угла $AED.$

Источники: БИБН-2020, 11.4 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1

У нас есть пары равных сторон и равные уголки... Какие равные треугольники можно здесь найти?)

Подсказка 2

AOC и BOD! Теперь подумаем про биссектрису AED. Что означает, что точка лежит на биссектрисе угла?

Подсказка 3

Что точка равноудалена от сторон! А теперь найдите эту точку, зная то, что AOC равен BOD)

Показать доказательство

$PIC$

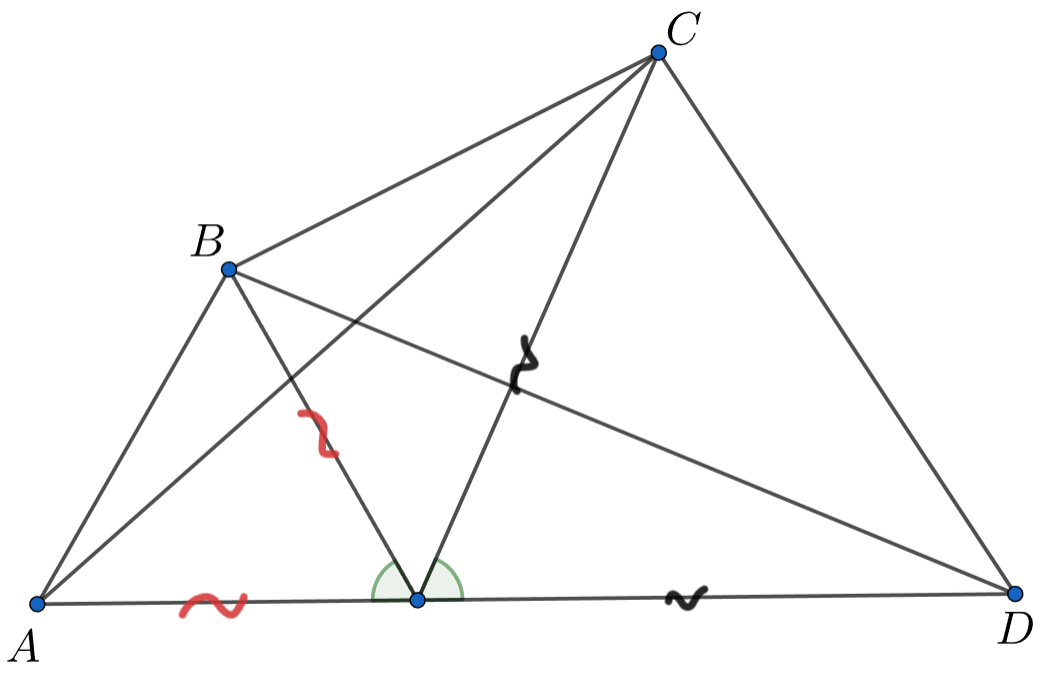
Сделаем поворот в точке $O$ на угол $AOB.$ Заметим, что треугольник $AOC$ перешёл в треугольник $BOD.$ Значит, эти треугольники равны. Следовательно, их высоты, проведённые к $AC$ и $BD$ равны.

Ошибка.
Попробуйте повторить позже

Задача 6#68255

На боковых сторонах $AB$ и $CD$ трапеции $ABCD$ взяты точки $M$ и $N$ соответственно, такие, что $AN = BN$ и $∠ABN = ∠CDM$ . Докажите, что $CM = MD$ .

Подсказки к задаче

Подсказка 1

Как мы хотим доказывать равенство отрезков CM и MD? У нас на картинке уже отмечены два уголка, а также есть параллельные прямые. Может, тогда попробовать доказать равенство углов MCD и MDC...

Подсказка 2

Что можно сказать про четырехугольник AMND? В нём мы уже знаем что-то про уголочек MDN, а уголочек MAN совпадает с углом BAN...

Подсказка 3

Т.к. BN равно AN, равны углы BAN и ABN, а ABN равен CDM по условию. Тогда четырехугольник AMND вписан. Что мы можем сказать про четырехугольник MBCN, если вспомнить, что AD параллельна BC...

Подсказка 4

Т.к. AD параллельна BC, углы CBА и BAD в сумме равны 180°. Т.к. AMND вписанный, MAD+MND=180°. Тогда CBM=CBA=180°-BAD=180°-MAD=MND. Это означает, что MBCN- вписанный четырехугольник. Осталось только перекинуть уголок MBN на MCN и завершить решение.

Показать доказательство

Из равенства $AN =BN$ следует, что $∠ABN = ∠BAN$ в равнобедренном треугольнике $ABN$ .

$PIC$

Тогда по условию задачи $∠CDM = ∠BAN?$ и значит? около четырехугольника $AMND$ можно описать окружность. Поэтому $∘ ∠MAD = 180 − ∠MND = ∠CNM$ .

В трапеции углы при боковой стороне дают в сумме $∘ ∘ 180 =⇒ ∠MAD = 180 − ∠MBC$ . Таким образом, в четырехугольнике $MBCN$ сумма углов при вершинах $B$ и $N$ тоже равна $∘ 180$ и поэтому около $MBCN$ можно описать окружность. Следовательно, $∠MCN = ∠MBN = ∠CDM$ , а значит, треугольник $CMD$ тоже равнобедренный, и $CM = MD$ .

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#69042

Дан треугольник $ABC$ , вписанный в окружность $ω$ . Точка $M$ — основание перпендикуляра из точки $B$ на прямую $AC$ , точка $N$ — основание перпендикуляра из точки $A$ на касательную к $ω$ , проведенную через точку $B$ . Докажите, что $MN ∥BC$ .

Источники: БИБН - 2016, 11.3

Показать доказательство

$PIC$

Рассмотрим четырехугольник $ANBM$ . Около него можно описать окружность (с диаметром $AB$ , так как углы $ANB$ и $AMB$ — прямые). Значит, $∠BNM =∠BAC$ (по свойству вписанных углов). Далее, угол между касательной через точку $B$ и хордой $BC$ также равен углу $BAC$ (по свойству угла между касательной и хордой). Таким образом, отрезки $NM$ и $BC$ имеют одинаковые углы с касательной и поэтому параллельны.

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Предыдущий раздел

Следующий раздел