Треугольник с углом в 45 градусов
Ошибка.
Попробуйте повторить позже
и
— высоты остроугольного треугольника
в котором
Точки
и
— соответственно центр
описанной окружности и ортоцентр треугольника
Докажите, что прямая
проходит через середину отрезка
Подсказка 1
Угол в 45 градусов…Где же он встречается…Ого, а что насчет треугольников BA1A и BC1C? Что про них можно сказать? А что это дает?
Подсказка 2
Верно, они прямоугольные и равнобедренные, но тогда высоты в этих треугольниках - это серединные перпендикуляры. А значит пресечения высот в этих треугольниках - центр описанной окружности треугольника ABC. Нам нужно доказать, что в четырехугольнике C1OA1H точкой пересечения диагоналей, диагональ OH делится пополам. А где еще мы что-то очень похожее слышали? Что можно сказать про этот четырехугольник?
Подсказка 3
Поскольку данный четырехугольник образован серединными перпендикулярами и высотами в одном треугольнике, то данный четырехугольник является параллелограммом. А что мы знаем насчет диагоналей параллелограмма?
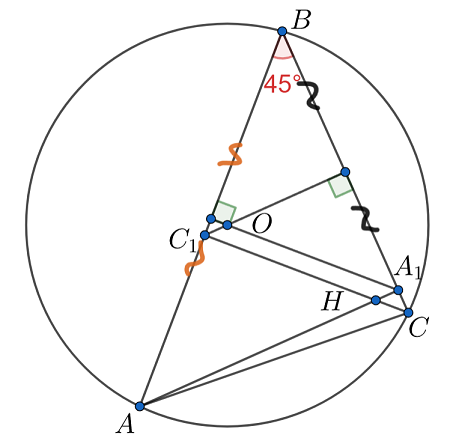
По условию а значит,
и
— равнобедренные. Отсюда
лежит на серединном перпендикуляре к
а
— на серединном перпендикуляре к
Также на обоих перпендикулярах находится точка
Но тогда
откуда
Аналогично
откуда
— параллелограмм, а значит
делится
пополам.
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике с углом
при вершине
проведены высоты
и
Луч
пересекает прямую
в точке
Оказалось, что
Найдите углы треугольника
Источники:
Подсказка 1
Даны параллельность и вписанность - это сразу же намекает нам на углы! Попробуем поотмечать, а потом воспользуемся условием на угол A) Что узнаем?
Подсказка 2
Понимаем, что AF = FC! Теперь мы можем посчитать достаточно большое количество углов на картинке...но все из них равны либо 90, либо 90/2. На что это может намекать? Обратим внимание на точку F.
Подсказка 3
Угол AFC в 2 раза больше чем AXC. Чем тогда является F для треугольника AXC? Когда мы это поймем, мы сможем по аналогии связать углы AFX=EFB и ACB. Не забываем про вписанность!)
![]()
Из условия следует, что . Из вписанностей
, и теперь из параллельности
. В треугольнике
точка
оказалась центром описанной окружности (равноудалена от вершин
и
и центральный угол в два раза больше вписанного).
Поэтому
, что вместе со вписанностью
дает



