Нетабличные углы
Ошибка.
Попробуйте повторить позже
Два треугольника пересекаются по шестиугольнику , в котором
Найдите углы этих треугольников.
Источники:
Случай (стороны треугольника - тройки несмежных сторон):
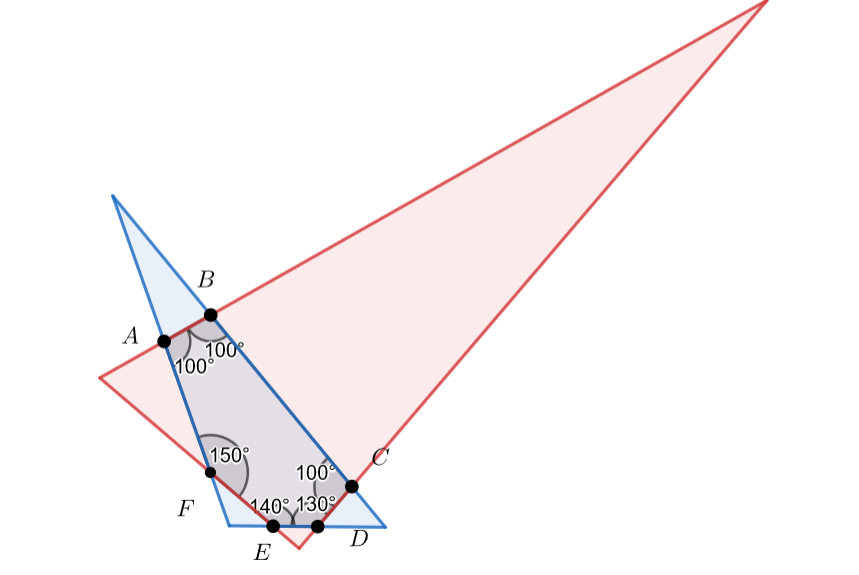
В таком случае все углы треугольников легко находятся, как , где
- два соседних угла
шестиугольника.
Тогда получаем, что углы красного треугольника равны , а углы синего -
.
Случай (один из углов шестиугольника совпадает с углом треугольника):
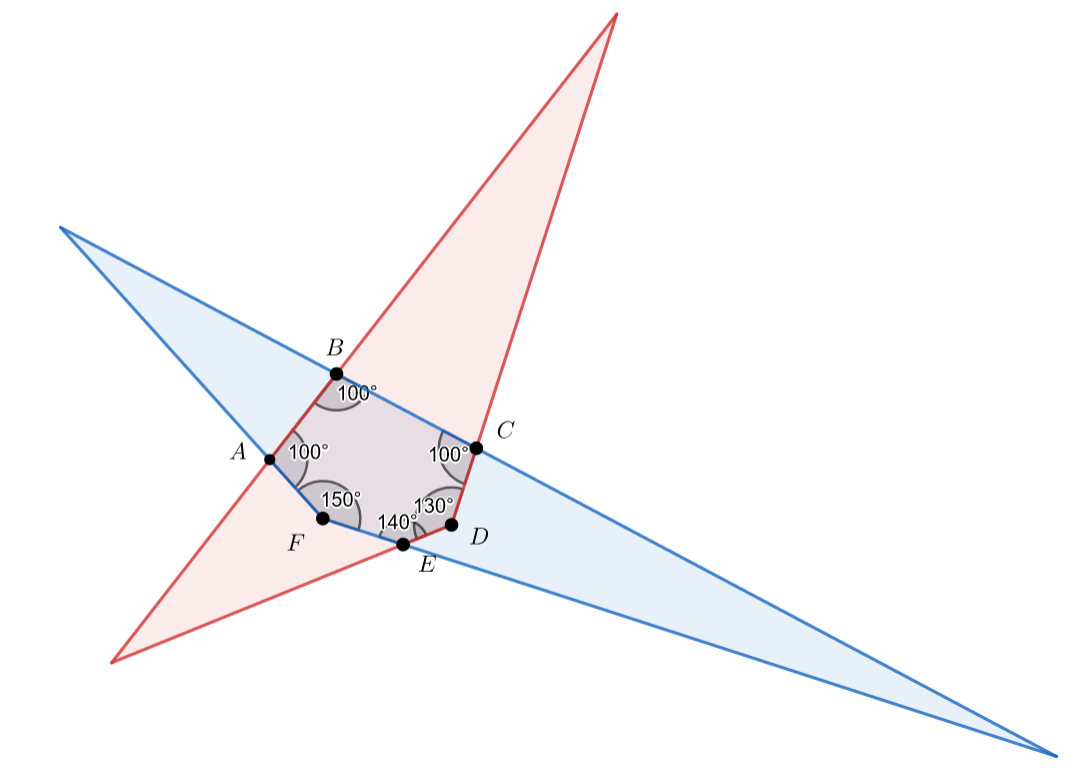
Заметим, что это единственное возможное положение в этом случае. Углы синего треугольника равны ;
и
.
Углы красного треугольника будут равны
и
.
и
; или
и
Ошибка.
Попробуйте повторить позже
Дан пятиугольник в котором
,
Найдите величину угла
(в градусах).
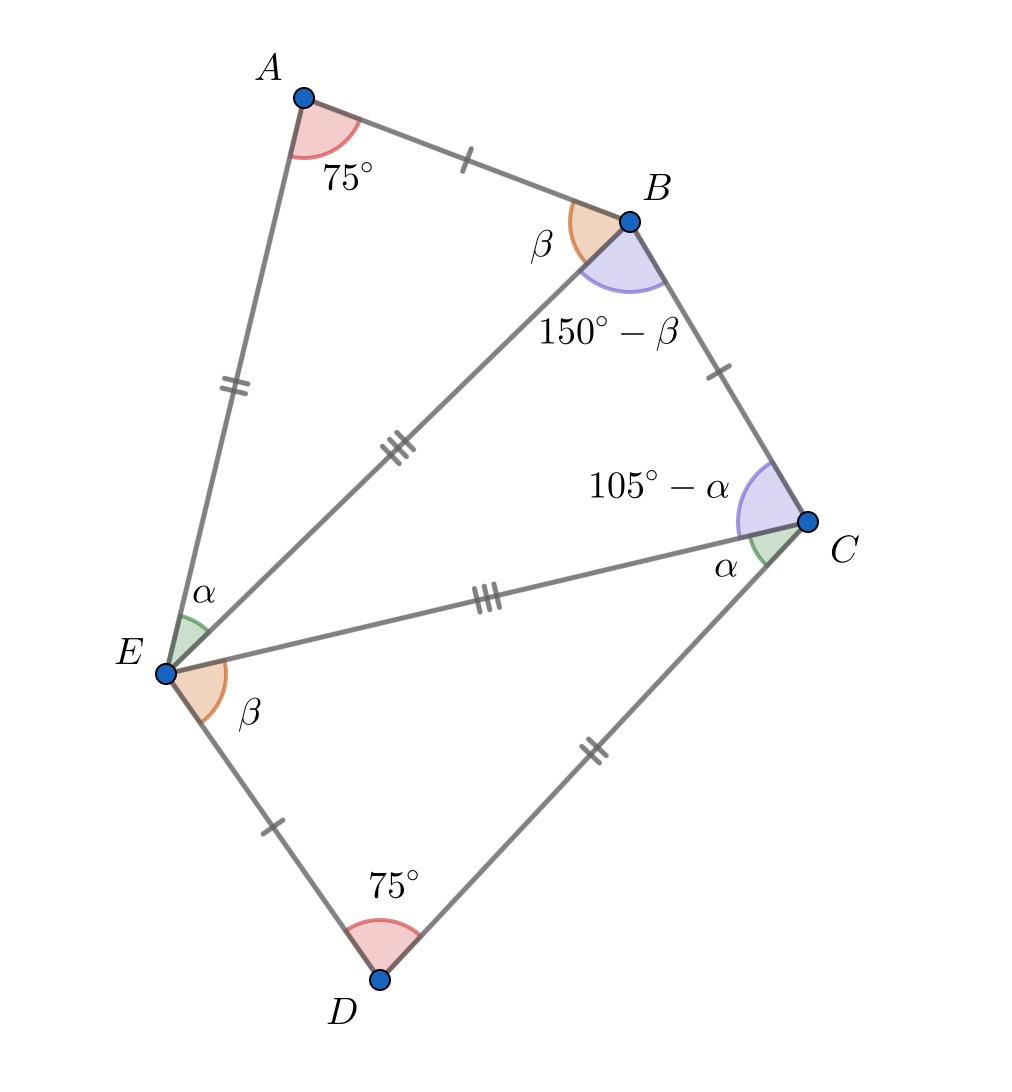
Заметим, что треугольники и
равны, так как
и
Следовательно,
то есть
треугольник
равнобедренный. Пусть
и
тогда
и
но
поэтому
А из треугольника
получаем
Значит, Треугольник
равнобедренный, поэтому
В итоге
Ошибка.
Попробуйте повторить позже
Дан равнобедренный треугольник с углом при вершине, равным
. Точка
расположена внутри треугольника
так, что
, а
. Найдите величину угла
.
Источники:
Первое решение.
Пусть — высота/медиана/биссектриса треугольника. Пусть
— пересечение луча
и отрезка
.
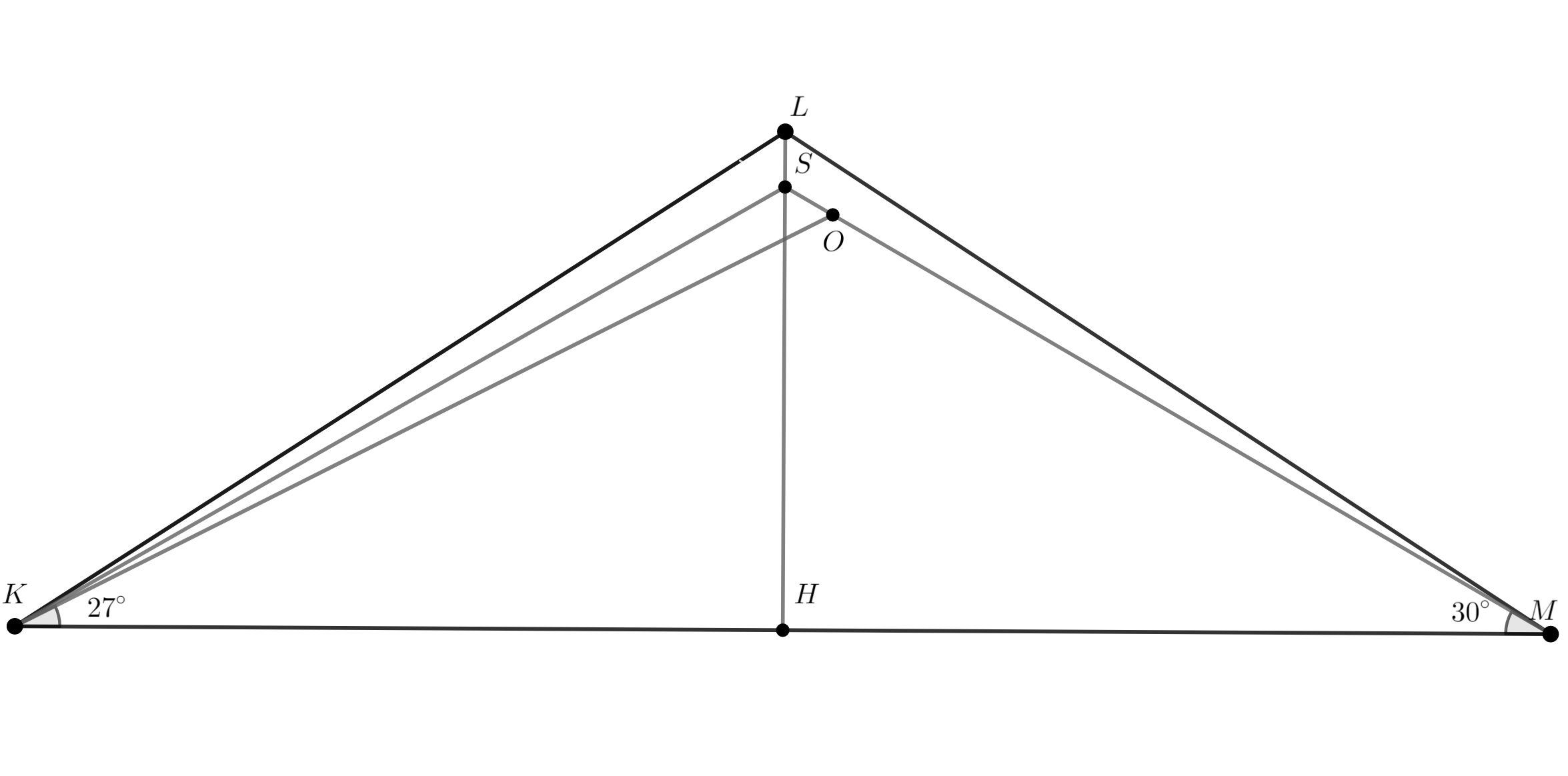
Заметим, что (поскольку в треугольнике
медиана
совпала с высотой).
Посчитаем углы: 1. ; 2.
; 3.
; 4.
;
5.
, а значит
; 6.
, а значит
.
Треугольники и
равны по общей стороне
и двум углам (пункты 5. и 6.) Следовательно,
, треугольник
равнобедренный. Значит,
________________________________________________________________________________________
Второе решение.

Несложно посчитать, что . Докажем, что
, а
. Для этого воспользуемся
тригонометрической формой теоремы Чевы. В соответствии с этой теоремой нам достаточно проверить, что
или . Это очевидно:
Осталось лишь вычислить из треугольника
.
Ошибка.
Попробуйте повторить позже
Внутри треугольника взята такая точка
что
Найдите:
a) углы и
б) расстояние между центрами окружностей, описанных около треугольников и
если
Источники:
a)
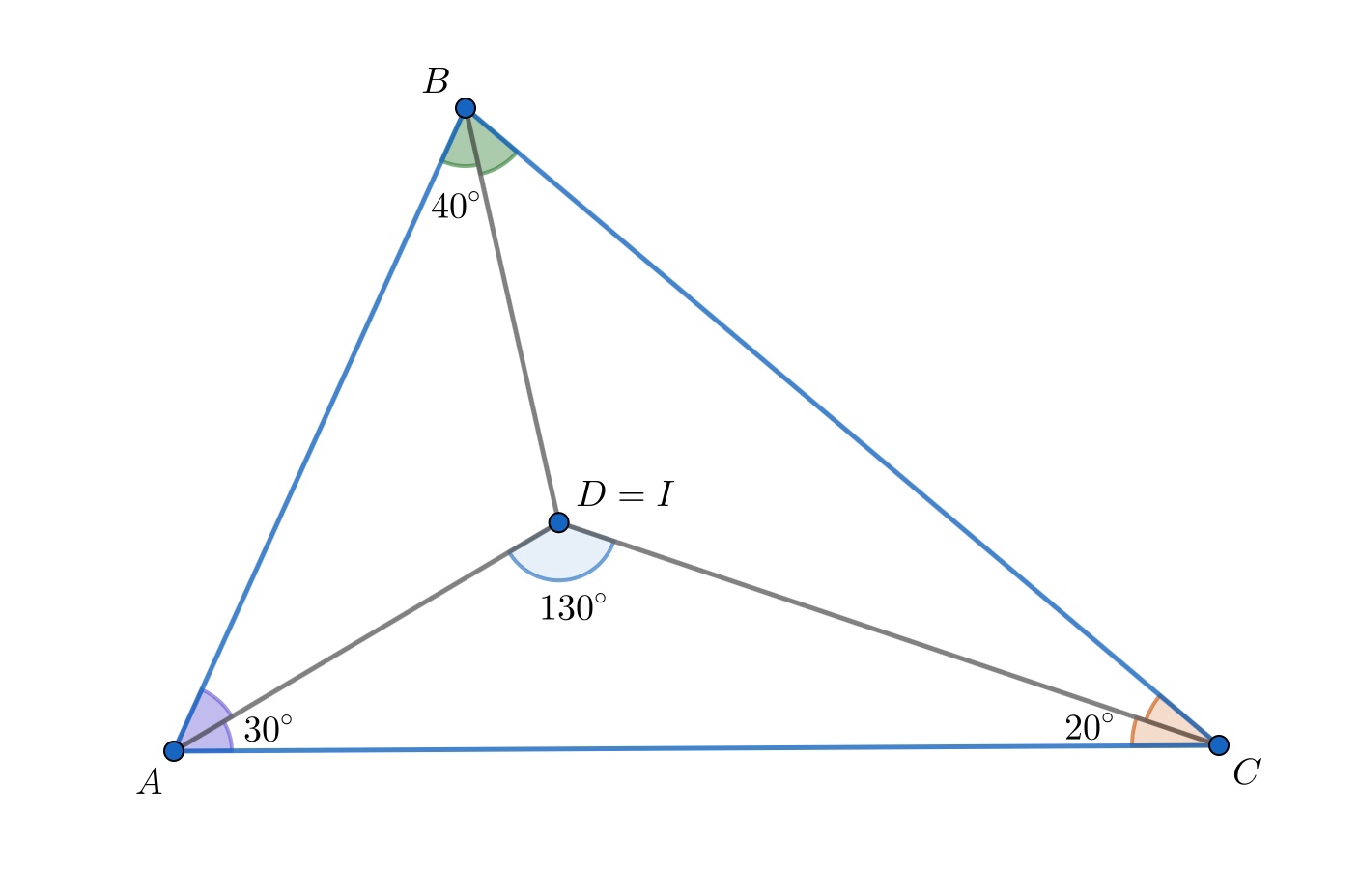
По теореме о сумме углов в треугольнике Пусть
— центр вписанной в треугольник
окружности. Тогда угол между биссектрисами
Получается, что из точек
и
отрезок
виден под
одинаковым углом, тогда они лежат на одной окружности вместе с
. При этом из условия следует, что ещё они обе лежат на одной
прямой (на биссектрисе угла
), поэтому либо совпадают, либо являются противоположными вершинами прямоугольника (вписанного
параллелограмма)
. Но так как
то может быть только случай
Следовательно,
и
.
Замечание. Для доказательства можно было также воспользоваться условием, что точка
дана внутри треугольника, и
упростить часть рассуждений.
б)
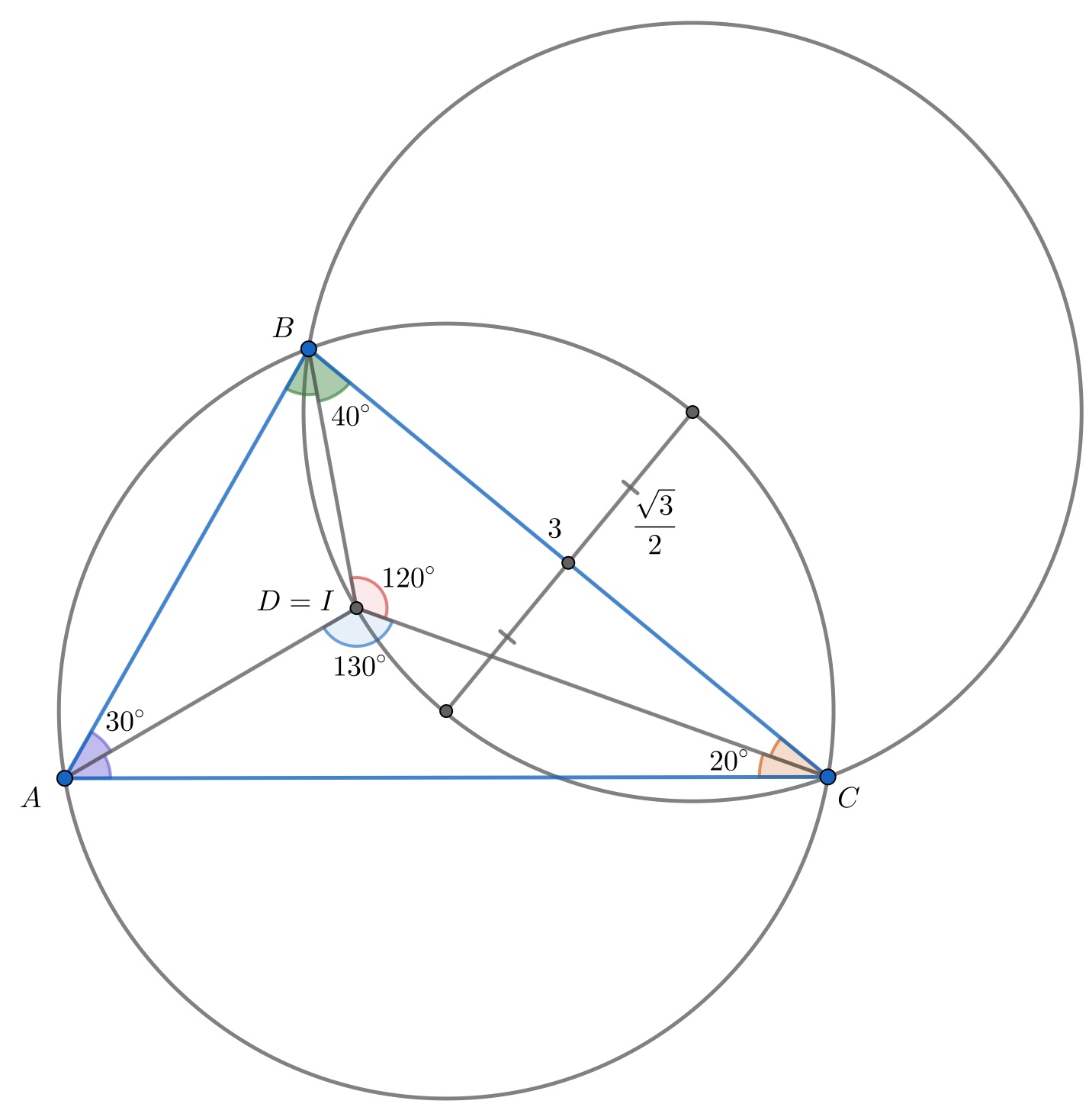
Радиус окружности, описанной вокруг треугольника , равен
Но
поэтому радиус окружности, описанной вокруг треугольника , также равен
Значит, их общая хорда пересекает отрезок между центрами в его середине, а длина этого отрезка равна
.
а) и
б)
Ошибка.
Попробуйте повторить позже
Про пятиугольник известно, что
Найдите
![]()
Давайте пересечем и
в точке
.
из равнобедренности
. Аналогично,
. Тогда
и из этого следует, что
. Значит,
. Аналогично,
.
![]()
Теперь посчитаем . Значит,
. Отсюда следует, что
,
,
.
Ошибка.
Попробуйте повторить позже
В выпуклом четырехугольнике
,
. На продолжении стороны
за точку
отложили отрезок
и
получили точку
. Оказалось, что
. Найдите угол между
и биссектрисой угла
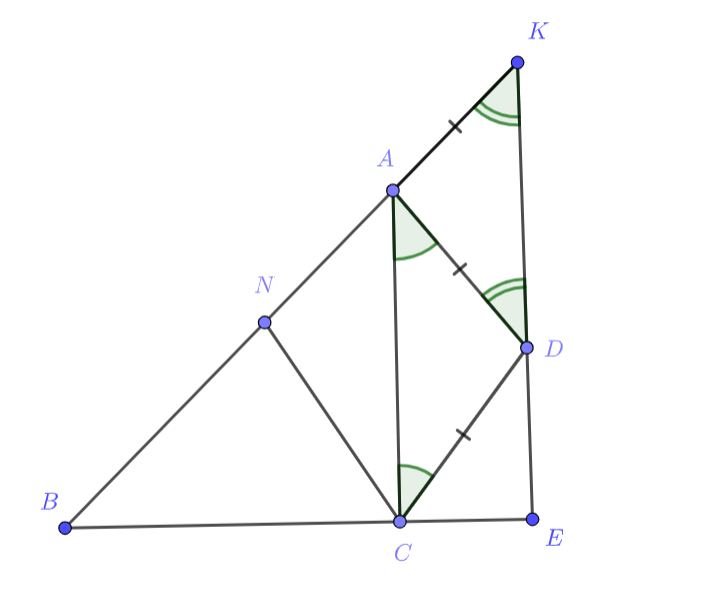
Пусть — точка пересечения
и
, причем
лежит на продолжении
за точку
. В треугольнике
угол
равен
, а внешний угол при вершине
равен
. Поэтому
и
. Следовательно треугольник
—
равнобедренный. Пусть
.
, поэтому
.
.
. Пусть
— биссектриса угла
, тогда
.
Замечание. Случай, когда точка лежит на отрезке
, разбирается аналогично, только некоторые знаки меняются на
противоположные.
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике (
) угол при вершине
равен
. На сторонах
и
отмечены точки
и
соответственно так, что
,
. Докажите, что
Первое решение.
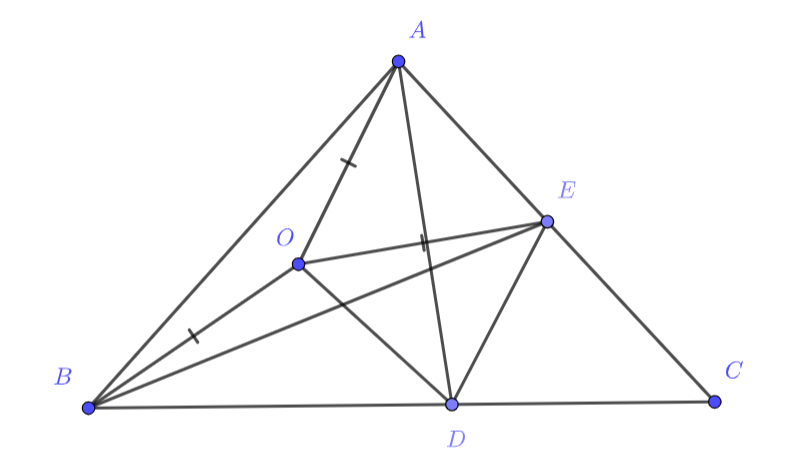
Пусть — центр описанной окружности треугольника
. Так как
, то
. Следовательно,
треугольник
— равносторонний.
в этом треугольнике является биссектрисой, поэтому треугольники
и
равны. Далее,
, откуда
; следовательно, треугольники
и
равны по трем
сторонам. Заметим, что из
следует, что
. Наконец,
и
Второе решение.
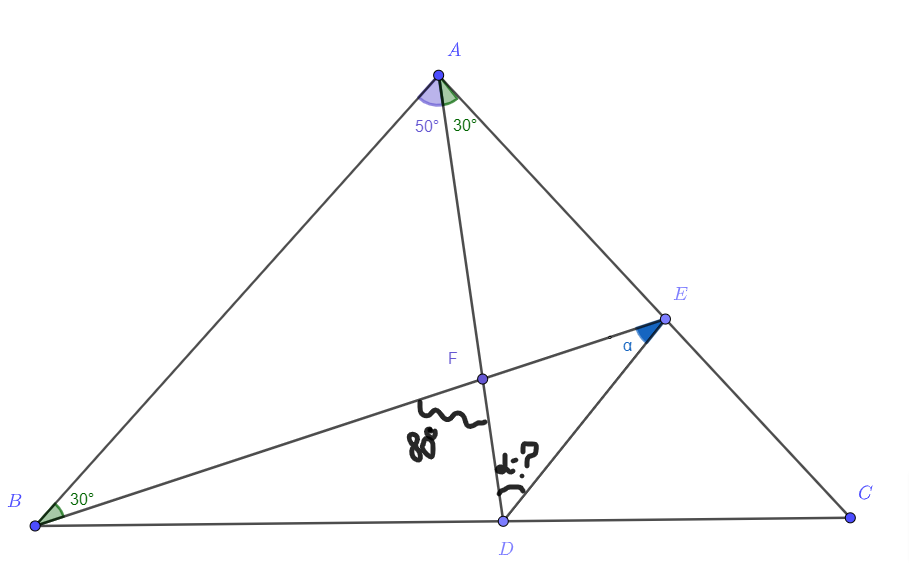
Обозначим точку пересечения и
за
Из условия сразу же находим внешний угол треугольника
:
. Нас просят доказать, что
тогда угол
тоже должен быть равен
Давайте не
будем думать и попробуем доказать
счётом в синусах:
В итоге
Третье решение.
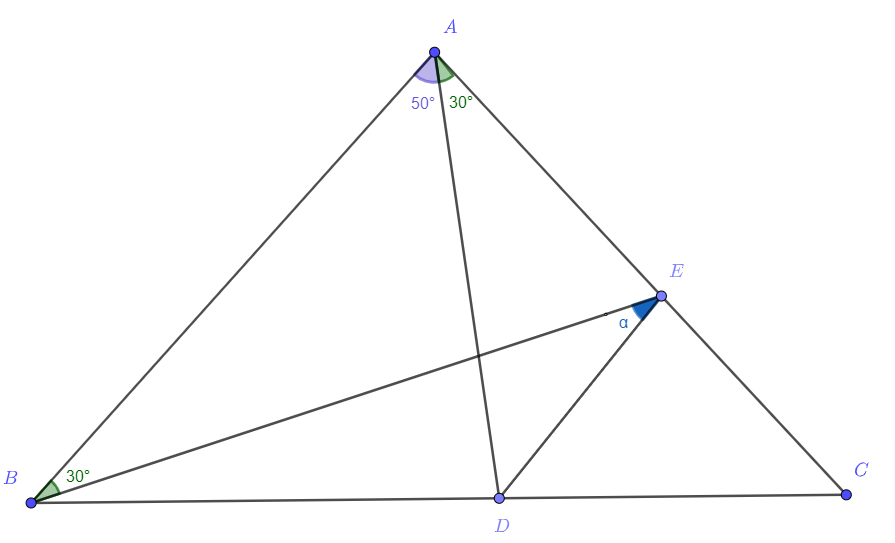
Обозначим Из условия находим
Замечаем, что
- равнобедренный, так как его углы
при основании
равны по
поэтому
Выразим
и
из теоремы синусов:
Перемножая каждую пропорцию крест-накрест, а затем равенства между собой, получаем:
Применим формулу синуса суммы:
Умножим на обе части, применим формулу приведения и перенесём второе слагаемое из правой части в левую часть:
Применим формулы синуса и косинуса двойного угла:
В итоге что и требовалось.
Ошибка.
Попробуйте повторить позже
Внутри треугольника , в котором
, взята точка
так, что треугольник
— равносторонний. Найдите
углы
и
Источники:
Опишем окружность около , тогда для её центра
выполнено
, при этом
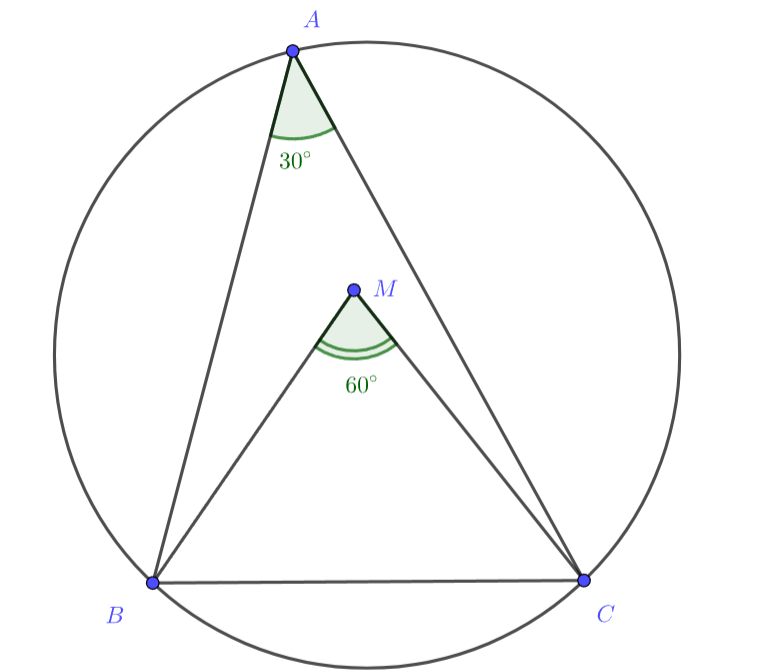
Получается, что является центром описанной окружности.
Далее легко посчитать


