Стереометрия на ФЕ
Ошибка.
Попробуйте повторить позже
На плоскости в ортогональной проекции изображена правильная пирамида (с основанием
) и высота
грани
как
показано на рисунке.
![]()
Как с помощью циркуля и линейки построить изображение центра сферы, описанной возле пирамиды?
Источники:
Подсказка 1
Для начала подумаем, вообще где должен быть центр сферы. Ну он лежит точно в плоскости, которая перпендикулярна ребру... А через какую точку на ребре будет проходить такая плоскость?
Подсказка 2
В нашем случае - через середину, а середину ребра мы точно сможем сделать) Теперь подумаем где еще может быть центр описанной окружности в правильной пирамиде. Например, на высоте) А эту высоту как раз можно найти в нашей плоскости. Но надо еще понять как построить само основание высоты...
Подсказка 3
В нашем случае, основание высоты будет также центром основания и пересечением медиан, которое мы точно умеем строить: просто пересекая медианы. Осталось найти еще бы одну прямую, что если пересечь ее с высотой, то получится нужная точка....
Подсказка 4
Напомню, что прямая AH перпендикулярна ребру SB, а у нас еще есть середина стороны...
![]()
Пусть - середина
- центр основания
Тогда центр описанной сферы лежит на
(поскольку пирамида правильная).
Проекция
строится как середина проекции
а проекция
– как точка, делящая проекцию
в отношении
Обозначим
через
прямую, параллельную
и проходящую через середину
Она проходит через центр описанной сферы:
и
перпендикулярны
так что
перпендикулярна
а также
пересекает
Проекция
строится как параллельный перенос
проекции
проходящий через середину проекции
Эта проекция пересекает проекцию
ровно в проекции центра описанной
сферы.
Ошибка.
Попробуйте повторить позже
В прямоугольном параллелепипеде отметили середину
медианы
треугольника
. Оказалось, что эта точка
удалена от прямых
и от грани
на расстояние 1 . Найдите объём параллелепипеда.
Источники:
Подсказка 1
Давайте для начала попробуем изучить картинку. Наша точка O равноудалена от прямых AD' и AB', следовательно она лежит на биссектрисе угла ∠D'AB'. Но по условию, O- середина медианы. Что мы тогда можем сказать про треугольник △D'AB'?
Подсказка 2
Верно, он равнобедренный! Тогда AD'=AB'. Значит и прямоугольные треугольники △AA'B' и △AA'D' равны по катету и гипотенузе. Нетрудно видеть, что расстояние от M до плоскости (ABCD) равно удвоенному расстоянию от O до этой же плоскости, т.е. 2. Давайте обозначим длину AB за x и попробуем выразить через нее остальные отрезки...
Подсказка 3
AB' и B'D' можно легко найти из теорем Пифагора. Тогда в треугольнике △D'AB' мы знаем все стороны ⇒ можем воспользоваться формулой для нахождения медианы AM. А что можно сказать про треугольники △AOX и △AB'M?
Подсказка 4
Точно, они подобны! Тогда B'M*AO/AB' = OX = 1, где X- основание перпендикуляра из O на AB'. Мы уже умеем выражать B'M, AO и AB' через x, поэтому мы сможем решить уравнение и найти x. Сделайте это и завершите решение!
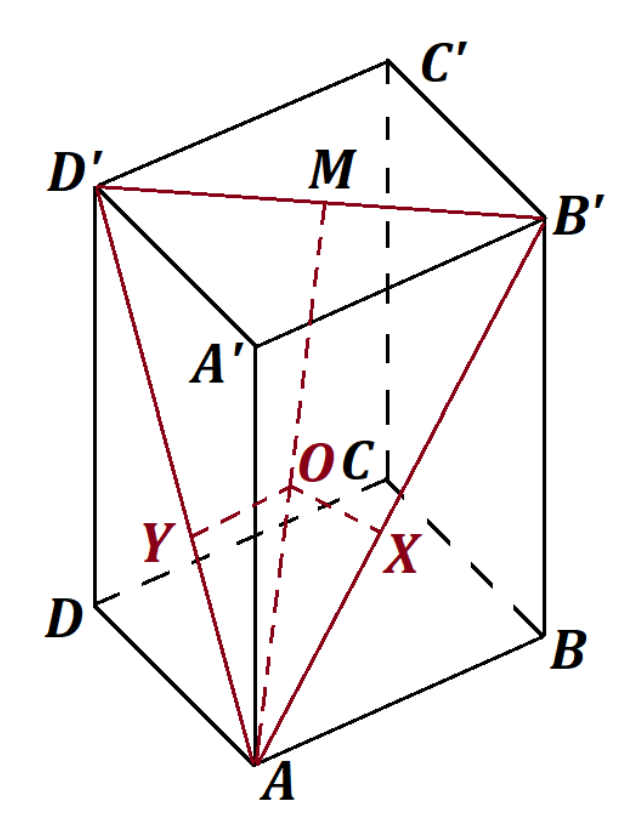
Пусть и
- это основания перпендикуляров, опущенных из
на
и
. Точка
на медиане
равноудалена от
сторон треугольника
, поэтому она лежит также на биссектрисе; значит, медиана является биссектрисой, поэтому
по катету и гипотенузе, тогда
Обозначим длины отрезков
и
через
и
.
Тогда
. Taкжe
Расстояние от точки до основания
в 2 раза меньше, чем расстояние от
до основания
то есть
,
откуда легко получается
и
то есть . Объём равен
.



