Тема Задачи №15 из ЕГЭ прошлых лет

№15 из ЕГЭ 2022

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#30767Максимум баллов за задание: 2

Решите неравенство

6 1 5x−-125-≤ 5x−-25.

Источники: ЕГЭ 2022, основная волна

Показать ответ и решение

Пусть $x 5 = t> 0.$ Тогда имеем:

6 1 6(t− 25)− (t− 125) 5t− 25 t− 125-≤ t−-25 ⇔ --(t−-125)(t−-25)--≤ 0 ⇔ (t−-125)(t−-25)-≤ 0

Применим метод интервалов:

$PIC$

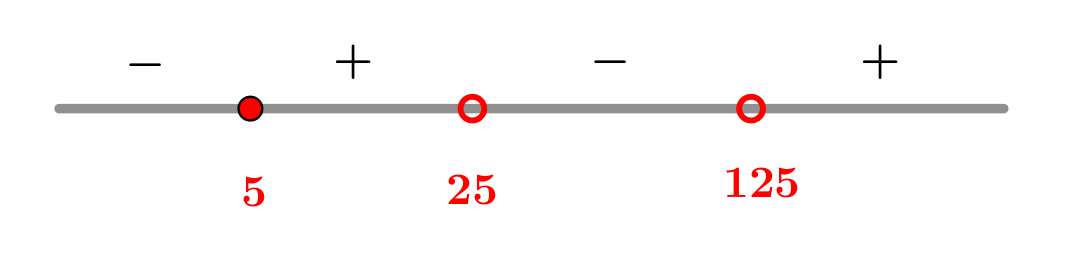
Тогда $t∈ (−∞; 5]∪ (25;125).$ Сделаем обратную замену:

⌊ ⌊ 5x ≤ 5 x≤ 1 ⌈ x ⇒ ⌈ 25< 5 <125 2< x< 3

Тогда окончательно имеем

x ∈(−∞; 1]∪(2;3)

Ответ:

$(− ∞;1]∪(2;3)$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#30768Максимум баллов за задание: 2

Решите неравенство

1 1 2x+-112-+ 2x−-128 ≥ 0.

Источники: ЕГЭ 2022, основная волна

Показать ответ и решение

Сделаем замену $x 2 = t$ и сведем неравенство к виду

1 1 t+-112 + t−-128 ≥ 0 t−-128+-t+-112≥ 0 (t+ 112)(t− 128) ----2t−-16----≥ 0 (t+ 112)(t− 128) -----t−-8----- (t+ 112)(t− 128) ≥ 0

Решим полученное рациональное неравенство методом интервалов, тогда

t∈ (− 112;8]∪(128;+ ∞ )

Сделаем обратную замену:

⌊ −112< 2x ≤ 8 ⌊x ≤ 3 ⌈ ⇔ ⌈ 2x > 128 x > 7

Таким образом, получаем $x ∈ (− ∞;3]∪ (7;+∞ ).$

Ответ:

$(−∞; 3]∪(7;+∞ )$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « $<$ » вместо « $≤$ » или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то выставляется оценка «0 баллов».

Ошибка.
Попробуйте повторить позже

Задача 3#30769Максимум баллов за задание: 2

Решите неравенство

2 1 3x-+27 ≥ 3x−-27

Источники: ЕГЭ 2022, основная волна

Показать ответ и решение

Сделаем замену $x 3 = t$ и сведем неравенство к виду

2 1 2(t− 27)− (t+27) t+-27 ≥ t−-27 ⇔ -(t+-27)(t−-27)--≥0 ⇔

⇔ ----t− 81----≥0 (t+ 27)(t− 27)

Решим полученное рациональное неравенство методом интервалов, тогда получим

t∈ (−27;27)∪ [81;+∞ )

Сделаем обратную замену:

⌊ x ⌊ ⌈ −27< 3 < 27 ⇔ ⌈x < 3 81 ≤ 3x x ≥ 4

Таким образом, подходят

x∈ (−∞; 3)∪[4;+ ∞)

Ответ:

$(− ∞;3)∪ [4;+∞ )$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 4#30770Максимум баллов за задание: 2

Решите неравенство

x 243 3 + 3x−-36 ≥ 0

Источники: ЕГЭ 2022, основная волна

Показать ответ и решение

Сделаем замену $x 3 = t$ и сведем неравенство к виду

243 t2− 36t+ 243 (t− 9)(t− 27) t+ t−-36 ≥ 0 ⇔ ---t− 36---≥ 0 ⇔ ----t− 36---≥ 0

Решим полученное рациональное неравенство методом интервалов, тогда

t ∈[9;27]∪ (36;+∞ )

Сделаем обратную замену:

⌊ x ⌊ ⌈9 ≤ 3 ≤ 27 ⇔ ⌈2≤ x ≤ 3 36< 3x log336 < x

Таким образом, получаем

x∈ [2;3]∪ (log336;+ ∞)

Ответ:

$[2;3]∪ (log336;+∞ )$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 5#26917Максимум баллов за задание: 2

Решите неравенство

√----- 1 log|x−5| x − 3 ≤ 4.

Источники: ЕГЭ 2022, досрочная волна

Показать ответ и решение

Выпишем ОДЗ данного неравенства:

(| (| |||| |x − 5|> 0 ||||x ⁄= 5 |{ |x − 5|⁄= 1 |{x ⁄= 6 || ⇔ || |||| x√−-3≥-0 ||||x ⁄= 4 ( x − 3> 0 (x > 3

Вернемся к решению исходного неравенства:

$pict$

Решим неравенство методом рационализации:

$pict$

Заметим, что

2 2 2 2 x − 7x + 14 = x − 2⋅3,5x +3,5 + 1,75= (x − 3,5) + 1,75 > 0

Тогда мы можем поделить на это выражение неравенство из первой системы. Получим следующее:

$pict$

Решим последнее неравенство методом интервалов:

x∈ [1;+∞ ) ⇔ x ≥1

Тогда совокупность примет вид

⌊ 5≤ x≤ 6 ⌈ ⇔ 1 ≤x ≤ 6 1≤ x< 5

С учетом ОДЗ окончательно получим $x ∈ (3;4)∪(4;5)∪(5;6).$

Ответ:

$(3;4) ∪(4;5)∪ (5;6)$

Ошибка.
Попробуйте повторить позже

Задача 6#26918Максимум баллов за задание: 2

Решите неравенство

log7(49x2)− 7 --log2x-− 4--≤ 1. 7

Источники: ЕГЭ 2022, досрочная волна

Показать ответ и решение

Найдем ОДЗ:

(| 2 ( ||{49x > 0 { x> 0 |x > 0 ⇔ ( 2 ||( 2 log7x ⁄= 4 (log7x− 4⁄= 0 ( ||x > 0 ||x > 0 |{ |{ ||log7x⁄= 2 ⇔ ||x ⁄= 49 |(log7x⁄= − 2 |(x ⁄= 149-

Вернемся к решению исходного неравенства. Преобразуем левую часть с учетом $x >0 :$

log7(49x2)− 7-= 2+-log7-x2− 7-= 2log7x−-5 log27x − 4 log27x − 4 log27x − 4

Тогда исходное неравенство примет вид

2log x − 5 log27x−-4-≤ 1 7

Обозначим $log x =t, 7$ тогда

$pict$

Решив последнее неравенство методом интервалов, получим

⌊ t= 1 t∈(− ∞;−2)∪ (2;+ ∞) ∪{1} ⇔ ||| ⌈t> 2 t< − 2

Сделаем обратную замену:

$pict$

С учетом ОДЗ получим

( 1) x∈ 0;49 ∪{7} ∪(49;+ ∞)

Ответ:

$( 1-) 0;49 ∪ {7}∪ (49;+∞ )$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2