№14 из ЕГЭ 2015
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде с основанием
известно, что
Точки
и
—
середины рёбер
и
соответственно. Плоскость
проходит через
и перпендикулярна плоскости
а) Докажите, что плоскость делит медиану основания
в отношении
считая от вершины
б) Найдите расстояние от точки до плоскости
Источники:
а) Пусть — проекция точки
на плоскость
и
— проекции на плоскость
точек
и
соответственно.
Плоскость проходит через
и
Пусть
— точка пересечения
и
— её проекция на плоскость
Тогда
лежит на
Так как — средняя линия в треугольнике
то
— середина
в силу подобия треугольников
и
по двум углам.
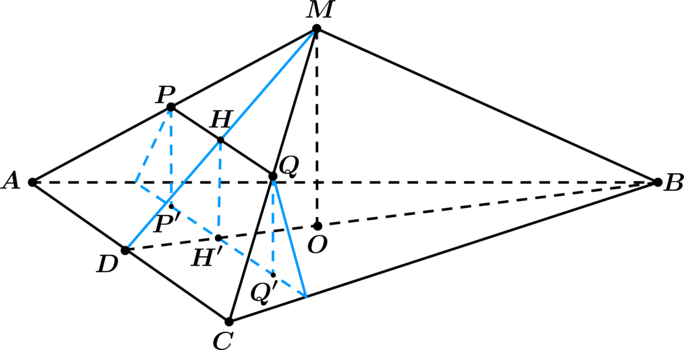
Рассмотрим прямоугольные треугольники и
В них
— общий, следовательно, треугольники
и
подобны по острому углу, откуда получаем
Так как пирамида правильная, то
— точка пересечения медиан треугольника
Следовательно,
имеем:
Отсюда получаем
Что и требовалось доказать.

б) Прямая параллельна прямой
и не лежит в плоскости
следовательно,
Обозначим искомое
расстояние через
Так как
то
Далее имеем:
Кроме того, Тогда получаем
и искомое расстояние равно
Найдём по теореме Пифагора в треугольнике
Тогда расстояние от точки до плоскости
равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании прямой призмы лежит квадрат
со стороной 4, а высота призмы равна
Точка
лежит на диагонали
причем
а) Постройте сечение призмы плоскостью
б) Найдите угол наклона этой плоскости к плоскости
Источники:
а) Назовем плоскость плоскостью
Пусть
— точка пересечения диагоналей грани
Тогда
Следовательно, вся прямая
Заметим, что прямые и
лежат в одной плоскости — плоскости
Пусть
— точка пересечения
прямой
и прямой
Тогда
Таким образом, получили точку пересечения плоскости
с гранью
Так как грани и
параллельны, то плоскость
пересечет их по параллельным прямым. Поэтому
проведем в грани
через точку
прямую параллельно
Пусть эта прямая пересекает ребра
и
в
точках
и
соответственно.
Таким образом, получили сечение призмы плоскостью
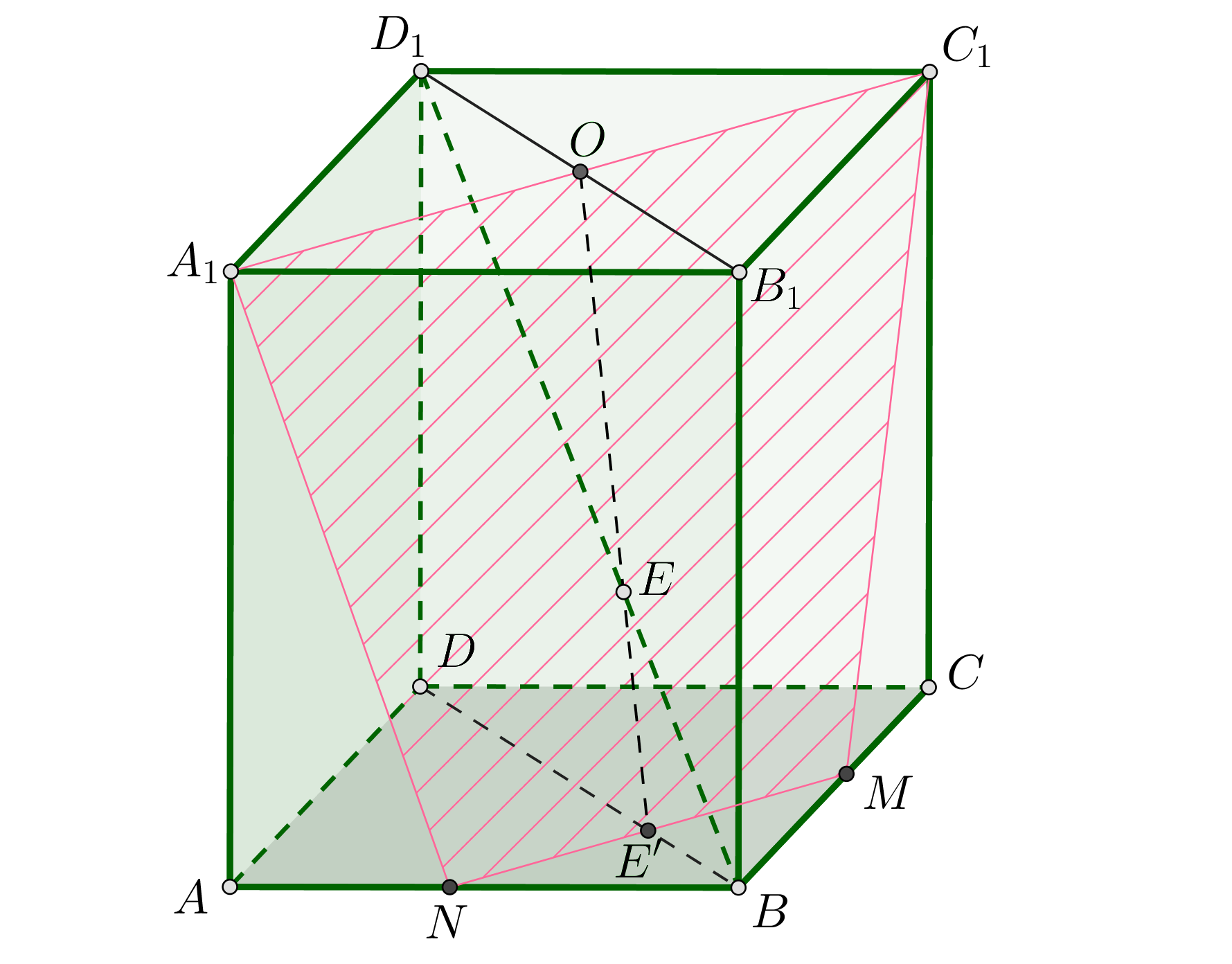
б) Так как основание призмы является квадратом, а диагонали квадрата перпендикулярны, то Так как
то
Необходимо построить линейный угол двугранного угла, образованного плоскостями и
то есть построить
перпендикуляры в каждой из плоскостей к их линии пересечения. Прямая
и есть линия их пересечения, следовательно, в
плоскости
уже найден перпендикуляр — это
Заметим, что по теореме о трех перпендикулярах прямая как наклонная, проекцией которой является прямая
Следовательно, необходимо найти
Рассмотрим сечение
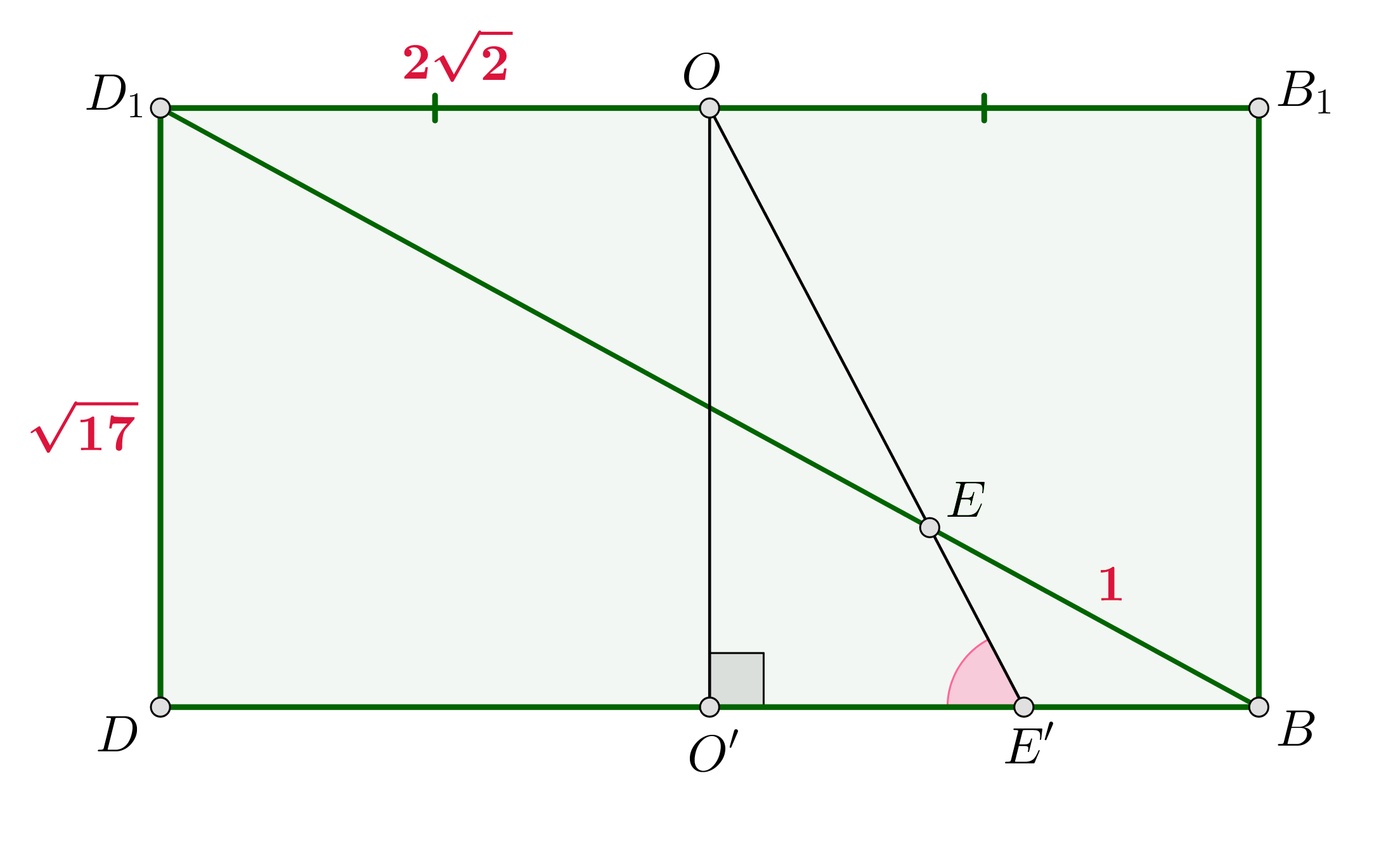
Проведем и найдем
Для этого нам нужно найти
так как
Заметим, что следовательно,
Тогда имеем:
Заметим также, что по двум углам. Следовательно,
Значит, получаем
Таким образом, имеем:
Тогда искомый угол равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Многогранник — куб. На ребре
отмечена точка
так, что
Через точки
и
проведена плоскость
параллельная прямой
а) Докажите, что где
— точка пересечения плоскости
с ребром
б) Пусть — точка пересечения плоскости
и прямой
Найдите угол
а) Рассмотрим треугольник Пусть
— точка на отрезке
такая, что
Плоскость
проходит
через точку
так как
и
проходит через точку
а
Тогда
— точка пересечения
и
Так как
то
Рассмотрим треугольники и
Они подобны по двум углам, откуда
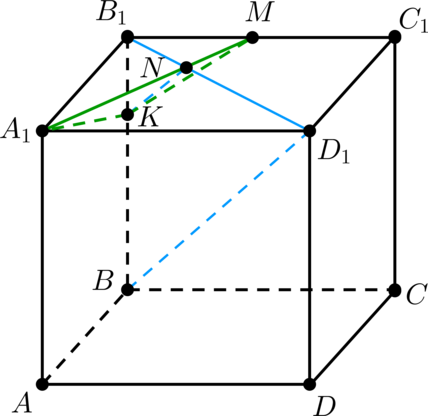
Следовательно,
Рассмотрим треугольники и
Так как
то
Следовательно, треугольники и
подобны по двум углам. Отсюда получаем
Тогда точка делит отрезок
в отношении
считая от вершины
б) Обозначим длину стороны куба через Из отношений, данных в условии, следует, что
Далее, отрезок как диагональ квадрата со стороной
По теореме Пифагора в треугольнике
В пункте а) уже было доказано, что с коэффициентом
Тогда имеем:

По теореме Пифагора в треугольниках и
соответственно имеем:
По теореме косинусов для треугольника
Тогда искомый угол равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основанием прямой четырёхугольной призмы является квадрат
со стороной
высота призмы
равна
Точка
— середина ребра
Через точки
и
проведена плоскость
параллельная прямой
a) Докажите, что сечением призмы плоскостью является равнобедренный треугольник.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью
Источники:
а) Рассмотрим треугольник Через точку
проведем среднюю линию
параллельную стороне
Тогда
точка
лежит в плоскости
Диагонали и
квадрата
точкой пересечения делятся пополам, то есть они пересекаются в точке
Тогда прямая
лежит в плоскости
значит,
— искомое сечение.
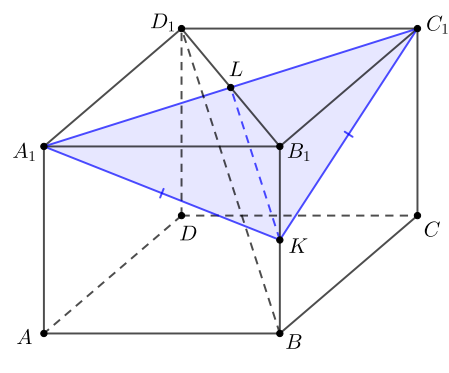
Рассмотрим прямоугольные треугольники и
У этих треугольников катеты
и
равны, а катет
— общий. Значит,
В равных треугольниках соответственные элементы равны, поэтому
следовательно, треугольник
— равнобедренный.
б) По теореме Пифагора в треугольнике
По теореме Пифагора в треугольнике
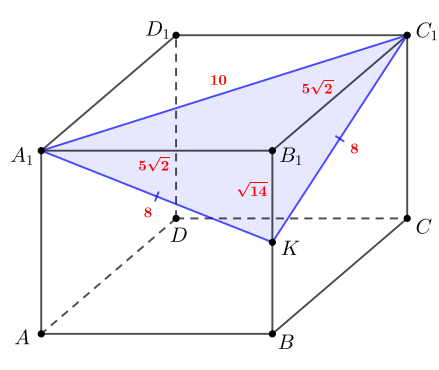
Тогда периметр треугольника
равен
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде все рёбра равны 5. На рёбрах
взяты точки
и
соответственно так, что
a) Докажите, что плоскость перпендикулярна ребру
б) Найдите расстояние от вершины до плоскости
Источники:
а) Докажем, что Рассмотрим треугольник
в плоскости
Он равносторонний, так как
и
по условию. Тогда
Треугольник равносторонний по условию, то есть
Тогда прямые
и
параллельны, так как
равны соотвественные углы
и
при прямых
и
и секущей
Рассмотрим треугольник Его стороны равны
и
как диагональ квадрата со стороной 5, то
есть
Тогда по обратной теореме Пифагора треугольник прямоугольный и
Следовательно,
так как
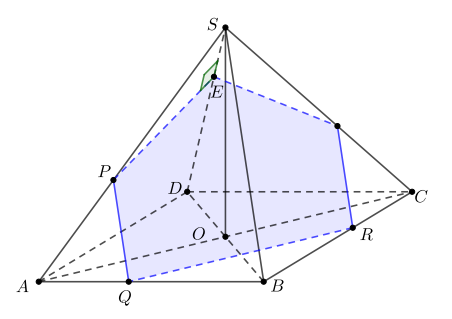
Докажем, что Рассмотрим треугольник
в плоскости
Он прямоугольный равнобедренный, так как
и
Тогда
Треугольник прямоугольный и равнобедренный, так как
— диагональ квадрата
Тогда
значит, прямые
и
параллельны.
Далее, диагональ квадрата
перпендикулярна диагонали
Пусть их пересечение — точка
Тогда
—
высота правильной пирамиды
то есть
Тогда по теореме о трех перпендикулярах Следовательно,
Получаем, что
и
значит,
б) В предыдущем пунке мы доказали, что Пусть плоскость
пересекает ребро
в точке
Тогда
расстояние от точки
до плоскости
равно длине отрезка
Поскольку то прямая
перпендикулярна любой прямой, лежащей в плоскости
в частности,

Рассмотрим треугольник в плоскости
В нем имеем:
Тогда отрезок равен
Значит, искомое расстояние равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде сторона
основания
равна 24, а боковое ребро
равно 19. Точки
и
— середины рёбер
и
соответственно. Плоскость
содержит прямую
и перпендикулярна плоскости
основания пирамиды.
a) Докажите, что плоскость делит медиану
основания в отношении
считая от точки
б) Найдите площадь многоугольника, являющегося сечением пирамиды плоскостью
Источники:
а) Пусть — проекция точки
на плоскость
и
— точки пересечения плоскости
с ребрами
и
соответственно. Плоскость
проходит через
и
Пусть — точка пересечения
и
— её проекция на плоскость
Тогда
лежит на
и
Так как — средняя линия в треугольнике
то
— середина
в силу подобия треугольников
и
по двум углам.
![]()
Рассмотрим прямоугольные треугольники и
У них
— общий, следовательно, треугольники
и
подобны по двум углам, откуда
Так как пирамида правильная, то
— точка пересечения медиан треугольника
следовательно,
Тогда получаем
б) Прямая параллельна плоскости
поэтому сечение пересекает плоскость
по прямой
параллельной
Тогда
— трапеция и
как средняя линия треугольника
Рассмотрим треугольники и
Они подобны, так как
и по предыдущему пункту их коэффициент
подобия равен
Значит,
Рассмотрим треугольник Он прямоугольный, тогда по теореме Пифагора
![]()
Поскольку — средняя линия треугольника
то
Тогда площадь трапеции равна
б) 104
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В кубе все ребра равны 5. На его ребре
отмечена точка
так, что
Через точки
и
проведена плоскость
параллельная прямой
а) Докажите, что где
— точка пересечения плоскости
с ребром
б) Найдите объем большей из двух частей куба, на которые он делится плоскостью
Источники:
а) Прямая параллельна плоскости, если плоскость содержит прямую, параллельную данной. Поэтому проведем в плоскости
, содержащей
, прямую
. Пусть
– точка пересечения с отрезком
.
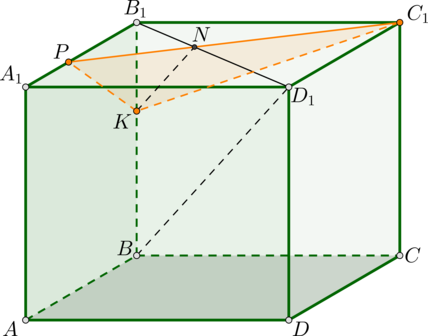
Соединив точки и
, получим прямую, пересекающую
в точке
.
Т.к. , то по теореме Фалеса
Теперь рассмотрим грань .
, следовательно,
Следовательно, и
.
б) Для того, чтобы найти объем большей из частей, на которые плоскость поделила куб, найдем объем куба и вычтем из него
объем пирамиды .
Заметим, что если рассматривать эту пирамиду как пирамиду с вершиной и основанием
, то она является
прямоугольной (
). То есть
– ее высота,
– основание, являющееся прямоугольным
треугольником.
Объем куба
Тогда объем большей части равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В кубе все ребра равны 5. На его ребре
отмечена точка
так, что
Через точки
и
проведена плоскость
параллельная прямой
а) Докажите, что где
— точка пересечения плоскости
с ребром
б) Найдите угол наклона плоскости к плоскости грани
Источники:
а) Прямая параллельна плоскости, если плоскость содержит прямую, параллельную данной. Поэтому проведем в плоскости
содержащей
прямую
Пусть — точка пересечения с отрезком
Соединив точки
и
получим прямую, пересекающую
в точке
Так как то по теореме Фалеса
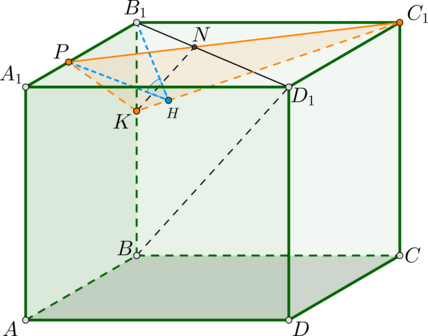
Теперь рассмотрим грань Так как
то
Следовательно,
б) Для того, чтобы найти угол между двумя плоскостями, необходимо построить линейный угол двугранного угла,
образованного этими плоскостями. Так как — линия пересечения этих плоскостей, то опустим перпендикуляр
на
Поскольку и наклонная
то по теореме о трех перпендикулярах проекция
Следовательно, по определению
— линейный угол двугранного угла, образованного данными плоскостями. Его и нужно
найти.
Заметим, что прямоугольный, отрезок
известен, следовательно, найдя отрезок
мы сможем найти тангенс
нужного угла.

Рассмотрим прямоугольный треугольник в котором
— высота. По теореме Пифагора имеем:
Следовательно,
Тогда найдем искомый угол:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде сторона основания
равна
, а боковое ребро
равно
. Точки
и
– середины ребер
и
соответственно. Плоскость
содержит
прямую
и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость делит медиану основания
в отношении
, считая от точки
.
б) Найдите расстояние от вершины до плоскости
.
Источники:
а) Две плоскости взаимно перпендикулярны, если одна из них содержит прямую, перпендикулярную
другой плоскости. Проведем прямую, принадлежащую плоскости и перпендикулярную плоскости
основания.
– медиана боковой грани,
– точка пересечения
и
,
– высота пирамиды
(по свойству правильной пирамиды высота падает в точку пересечения медиан основания).
Рассмотрим плоскость
. Проведем в ней прямую
. Тогда
так же, как и
, будет перпендикулярна
. Следовательно, плоскость
и есть плоскость
.
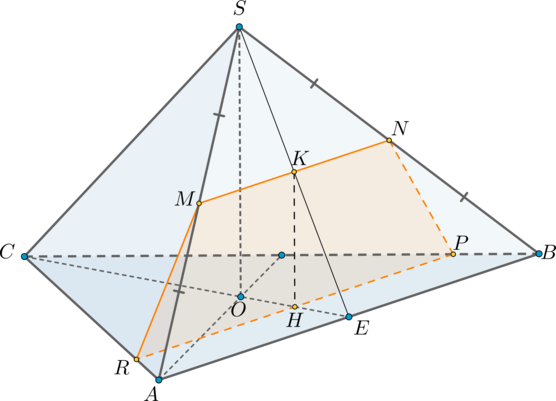
Построим сечение пирамиды этой плоскостью.
Плоскость пересечет плоскость
по прямой
, параллельной
, а значит и
.
Действительно, если
не параллельно
, то они пересекаются. Следовательно,
пересекает
и плоскость
, что невозможно, т.к.
по признаку (т.к.
). Таким образом,
– сечение пирамиды плоскостью
.
Заметим, что – середина
. По теореме Фалеса
Т.к. медианы точкой пересечения делятся в отношении , считая от вершины треугольника, то
. Следовательно,
. Следовательно,
, следовательно,
, откуда следует утверждение пункта а).
б) Прямая параллельна плоскости
(т.к.
), следовательно, расстояние от любой
точки прямой
до плоскости
одинаково. Поэтому будем искать это расстояние как расстояние от
точки
. Докажем, что
и есть искомое расстояние.
Во-первых, ,
, следовательно,
. Во-вторых, т.к.
, то
. Таким образом, мы нашли две пересекающиеся прямые в плоскости
(
и
),
перпендикулярные
. Следовательно, по признаку
.
Из пункта а) следует, что .
– высота в правильном треугольнике со стороной
,
следовательно,
Заметим, что в данной задаче условие “боковое ребро равно
” является лишним.
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основанием прямой четырехугольной призмы является квадрат
со стороной
высота призмы равна
Точка
— середина ребра
Через точки
и
проведена плоскость
параллельная прямой
а) Докажите, что сечение призмы плоскостью является равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью
Источники:
а) Прямая параллельна плоскости, если плоскость содержит прямую, параллельную данной. Поэтому проведем в плоскости
содержащей
прямую
Пусть — точка пересечения с отрезком
Так как
то по теореме Фалеса
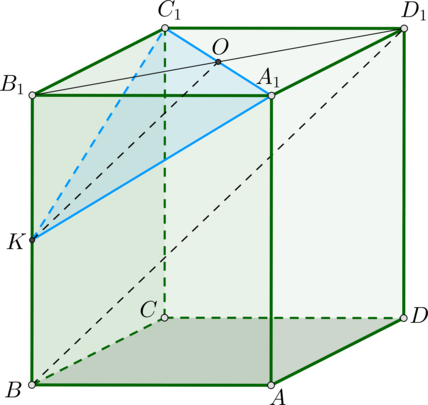
Следовательно, — середина
Так как
— квадрат, то его диагонали точкой пересечения делятся пополам,
следовательно,
содержит
Таким образом, треугольник — искомое сечение. Из равенства боковых граней следует, что отрезки
и
равны, то есть треугольник
равнобедренный.
б) Найдем отрезок по теореме Пифагора:
Диагональ квадрата равна стороне квадрата, умноженной на следовательно,
Таким образом, искомый периметр равен
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |


