№14 из ЕГЭ 2025
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме отметили точки
и
на
ребрах
и
соответственно. Известно, что
Через точки
и
провели плоскость
перпендикулярно грани
а) Докажите, что плоскость проходит через вершину
б) Найдите площадь сечения призмы плоскостью
если все
ребра призмы равны 12.
Источники:
а) Так как призма правильная, то — равносторонний треугольник.
Следовательно, медиана
является также и высотой треугольника
.
Отсюда
Также так как призма правильная, то
Получили, что перпендикулярна двум пересекающимся прямым из
плоскости
следовательно,
Так как
и
то
Что и
требовалось доказать.
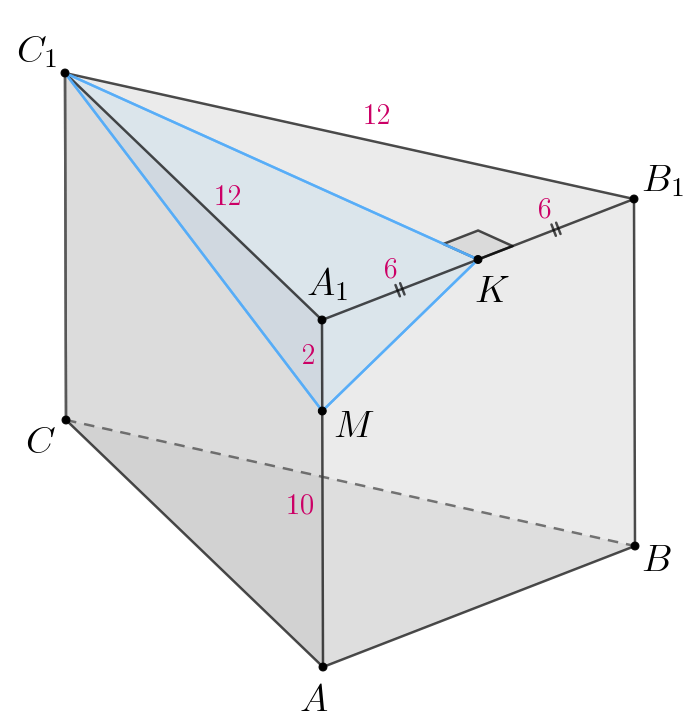
б) Выше мы доказали, что Но тогда
следовательно,
— прямоугольный треугольник и его площадь можно найти
по формуле:
Так как все ребра призмы равны 12, то Далее, из того, что
получаем
Тогда по теореме Пифагора для
По теореме Пифагора для
Тогда искомая площадь равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме отметили точки
и
на
ребрах
и
соответственно. Известно, что
Через точки
и
провели плоскость
перпендикулярно грани
а) Докажите, что плоскость проходит через вершину
б) Найдите площадь сечения призмы плоскостью
если все
ребра призмы равны 20.
Источники:
а) Так как призма правильная, то — равносторонний треугольник.
Следовательно, медиана
является также и высотой треугольника
.
Отсюда
Также так как призма правильная, то
Получили, что перпендикулярна двум пересекающимся прямым из
плоскости
следовательно,
Так как
и
то
Что и
требовалось доказать.
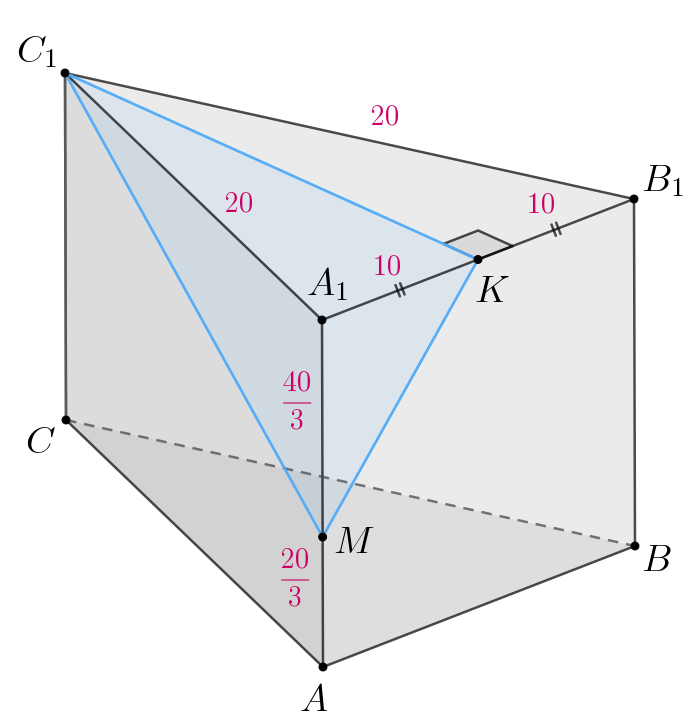
б) Выше мы доказали, что Но тогда
следовательно,
— прямоугольный треугольник и его площадь можно найти
по формуле:
Так как все ребра призмы равны 20, то Далее, из того, что
получаем
Тогда по теореме Пифагора для
По теореме Пифагора для
Тогда искомая площадь равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной пирамиде через ребро
провели
плоскость
образующую сечение
где точки
и
– точки
пересечения плоскости
с боковыми рёбрами
и
соответственно.
Известно, что
а) Докажите, что точки и
делят рёбра
и
в отношении
считая от вершины
б) Найдите косинус угла между плоскостью основания и плоскостью
Источники:
а) Рассмотрим три попарно пересекающиеся плоскости:
Прямые
и
— их линии пересечения. Тогда эти прямые либо
пересекаются в одной точке, либо попарно параллельны. Так как
то
имеем:
Тогда
Отсюда следует, что
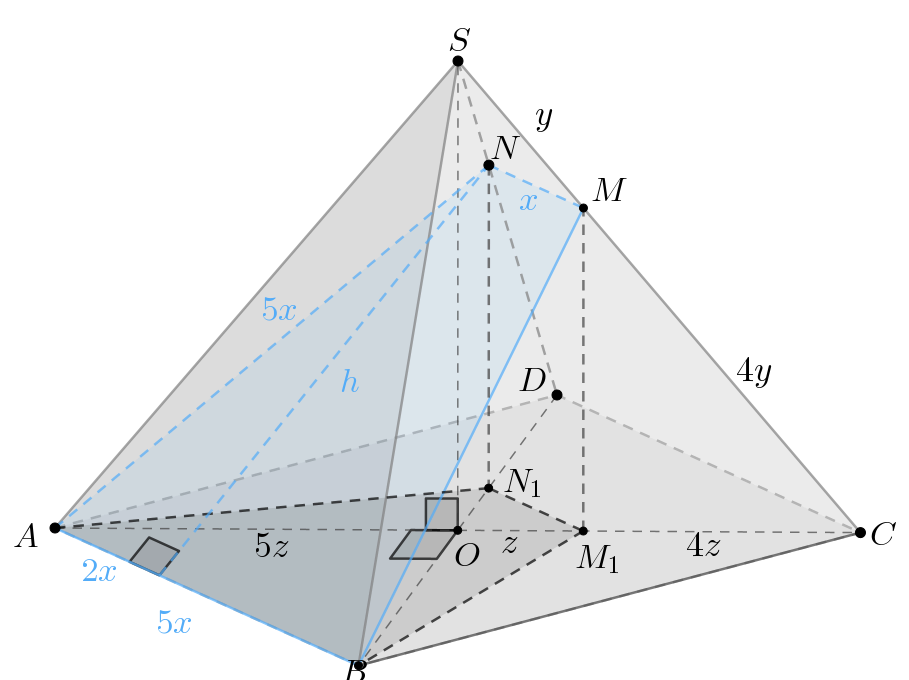
б) Пусть
Пусть — точка пересечения диагоналей
и
Так как пирамида
правильная, то
— высота этой пирамиды.
В плоскости проведем
Тогда
— проекция точки
на
плоскость
В плоскости проведем
Тогда
— проекция точки
на
плоскость
Значит, четырехугольник — проекция сечения
на плоскость
Если — угол между плоскостями
и
то
Рассмотрим Это равнобедренная трапеция. Пусть
— ее высота.
Тогда образуется прямоугольный треугольник с гипотенузой
и катетами
и
Следовательно, по теореме Пифагора:
Значит, площадь сечения равна
По теореме о пропорциональных отрезках
Аналогично
Пусть
Тогда
Диагонали и
четырехугольника
взаимно
перпендикулярны, следовательно, его площадь равна
Но по свойству квадрата
Отсюда площадь проекции сечения равна
Тогда искомый косинус равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде сторона основания
равна 3, а
боковое ребро
равно 5. На ребре
отмечена точка
а на продолжении
ребра
за точку
— точка
так, что
a) Докажите, что сечение пирамиды плоскостью
является
равнобедренным треугольником.
6) Найдите площадь сечения пирамиды плоскостью
Источники:
а) Пусть прямая пересекает ребро
в точке
Тогда
—
сечение пирамиды плоскостью
Докажем, что
Применим теорему Менелая для и прямой
Учитывая также, что получаем, что
Так как пирамида правильная, то боковые грани представляют собой равные
равнобедренные треугольники. Следовательно,
Тогда по двум сторонам и углу между ними:
Отсюда следует, что
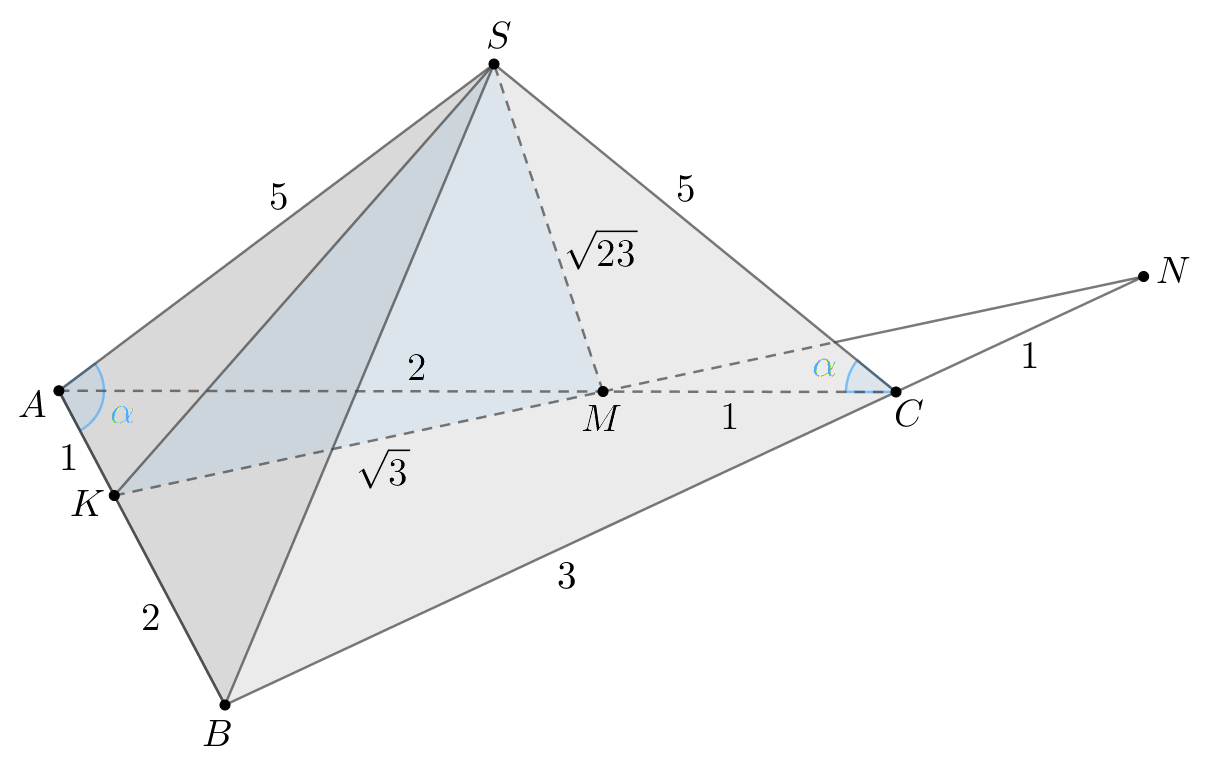
б) Из теоремы косинусов для следует, что
Применим теорему косинусов для
Так как — правильный, то
Применим теорему косинусов для
Рассмотрим Проведем высоту
Тогда она является и медианой,
следовательно,
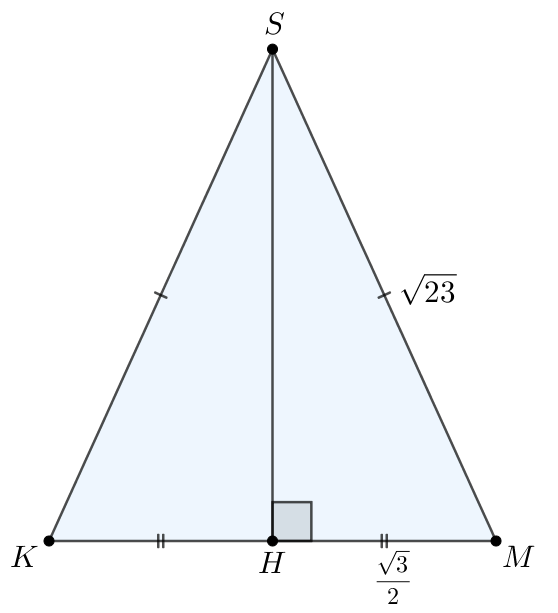
По теореме Пифагора для
Следовательно, площадь сечения равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде с основанием
известно, что
Через точку
пересечения диагоналей основания
перпендикулярно ребру
провели плоскость
а) Докажите, что плоскость проходит через вершины
и
б) В каком отношении плоскость делит ребро
считая от вершины
если площадь сечения равна
Источники:
а) Прямая перпендикулярна плоскости
если она перпендикулярна двум
пересекающимся прямым из этой плоскости. Поэтому найдем две прямые,
проходящие через точку
и перпендикулярные
Так как пирамида правильная, то — ее высота,
Тогда по
теореме о трех перпендикулярах
Так как
то
Что
и требовалось доказать.
Найдем вторую прямую. Проведем в высоту
то есть
Тогда
— сечение пирамиды плоскостью
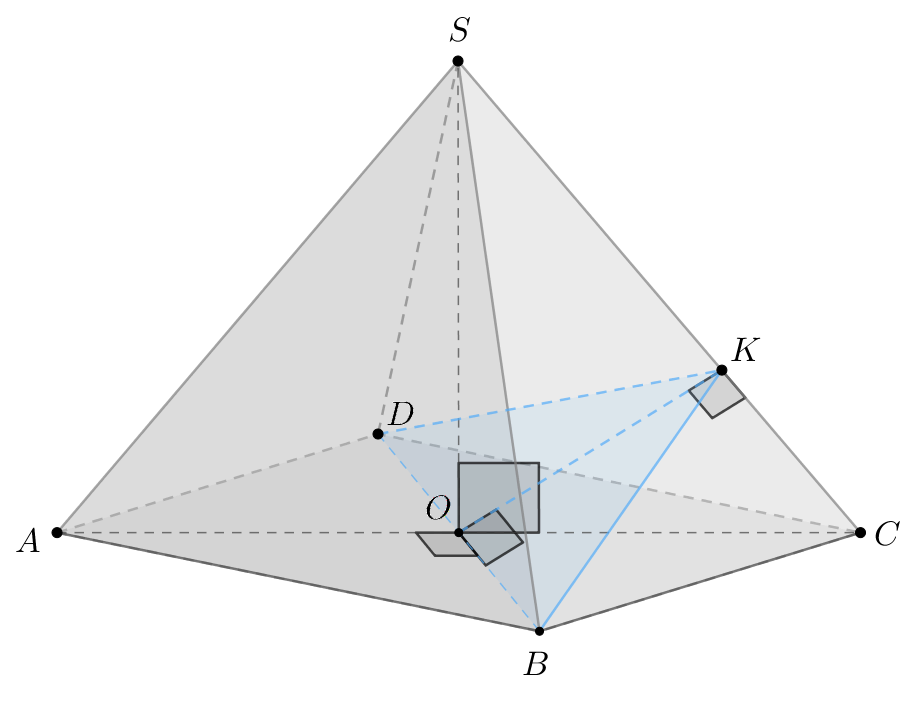
б) Требуется найти
По доказанному в пункте а) имеем:
Следовательно,
Тогда
Следовательно, площадь сечения равна
Так как и
— квадрат, то
Тогда площадь сечения равна
Перейдем в Пусть
Тогда из
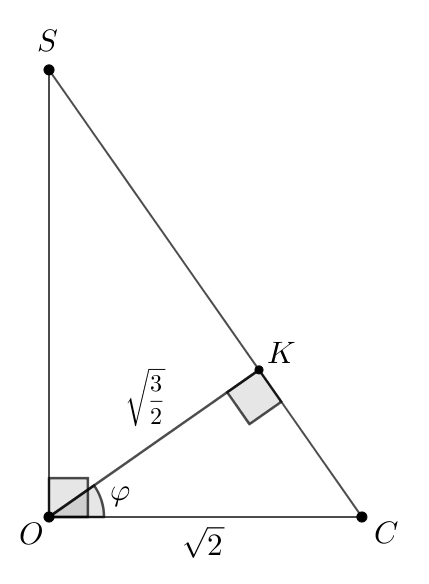
Тогда
По свойству прямоугольного треугольника и высоты, опущенной из прямого
угла, имеем: Следовательно,
Тогда имеем:
Значит, искомое отношение равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Плоскость перпендикулярна плоскости основания
правильной
четырёхугольной пирамиды
и пересекает ребро
в точке
Сечение пирамиды плоскостью
является правильным треугольником площадью
а) Докажите, что плоскость перпендикулярна прямой
б) В каком отношении точка делит ребро
считая от точки
если
объём пирамиды равен
Источники:
а) Проведём параллельно
тогда
Здесь
— высота
пирамиды, при этом так как
— правильная, то
— точка пересечения
диагоналей основания
Так как по условию
то прямая
проходящая через точку
и перпендикулярная
лежит в
плоскости
Далее, плоскости и
имеют общую точку
Тогда эти
плоскости пересекаются по некоторой прямой. Пусть это будет прямая
где
— точки пересечения со сторонами
и
основания
соответственно.
Так как перпендикулярна плоскости основания, то
перпендикулярна
Покажем, что
перпендикулярна
- Из свойств квадрата
— биссектриса угла
- Из свойств правильного треугольника
высота
является и медианой, то есть
Тогда — медиана и биссектриса в треугольнике
а значит, является
и высотой. Тогда
то есть
перпендикулярна
плоскости
Что и требовалось доказать.
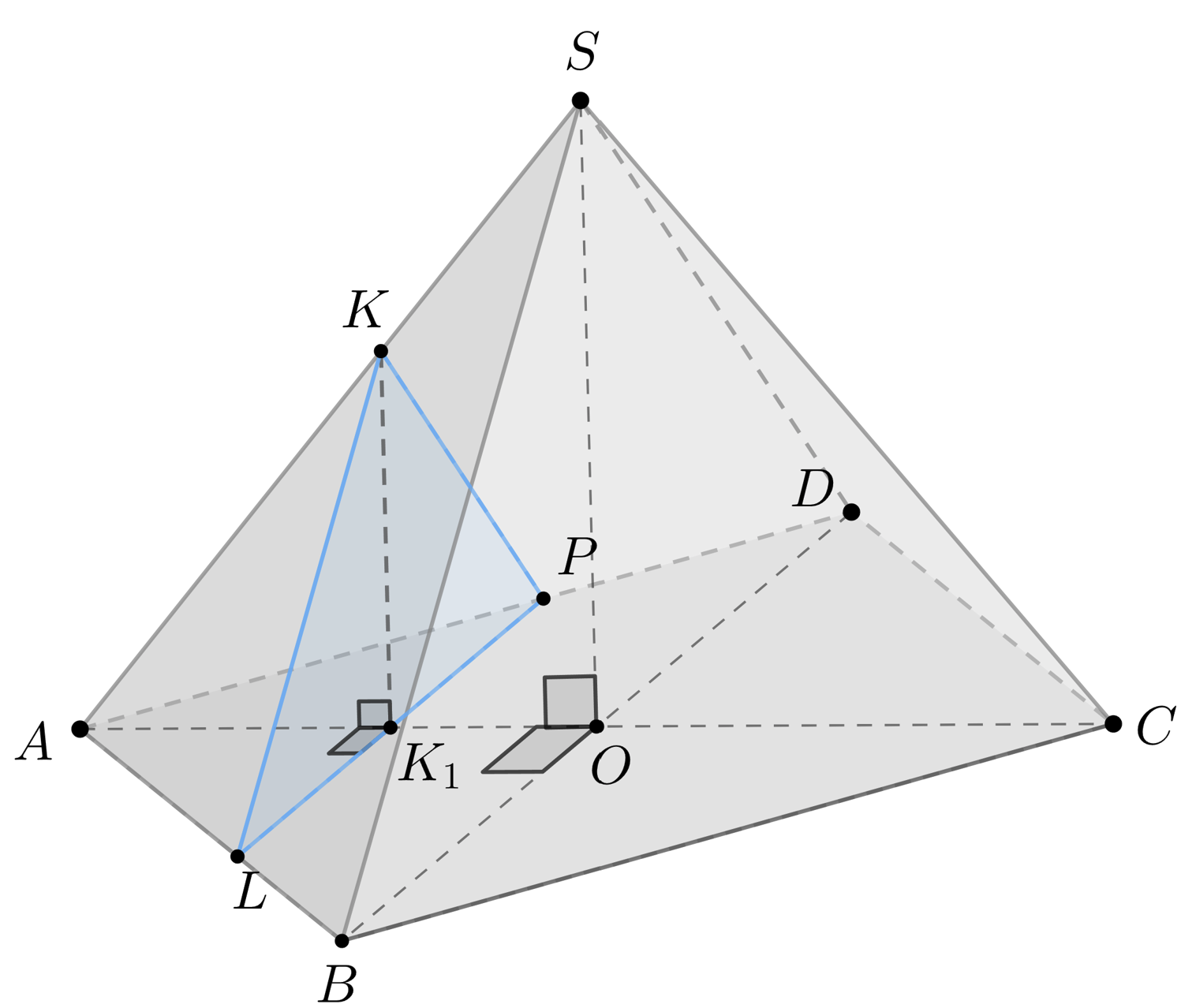
б) Распишем объёмы пирамид и
Выразим нужные отношения через Рассмотрим подобные по острому
углу прямоугольные треугольники
и
Запишем отношение подобия:
Найдем отношение площадей:
Из подобия по общему острому углу прямоугольных треугольников и
имеем:
Тогда получаем:
Чтобы найти запишем площадь правильного треугольника
Из
свойств правильного треугольника известно, что
Тогда
имеем:
Отсюда получаем, что
Из прямоугольного равнобедренного треугольника
Отсюда Найдем объем пирамиды
Тогда имеем:
Откуда получаем, что Отсюда если
то
и
Тогда искомое отношение равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
На ребрах
и
правильного тетраэдра
отмечены точки
и
соответственно. Известно, что
а) Докажите, что плоскость проходящая через точки
и
делит
ребро
в отношении
считая от вершины
б) Найдите площадь сечения тетраэдра плоскостью
если
Источники:
а) Так как то по обратной теореме о пропорциональных
отрезках
Пусть плоскость сечения пересекает
в точке
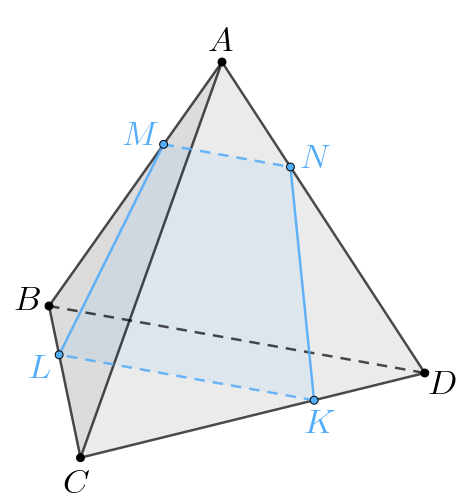
Линии пересечения трех попарно пересекающихся плоскостей либо попарно параллельны, либо пересекаются в одной точке.
Тогда рассмотрим плоскости
и
Они пересекаются
по прямым
и
Так как
то линии пересечения этих
плоскостей не могут пересекаться в одной точке. Следовательно, они попарно
параллельны:
Отсюда Тогда по теореме о пропорциональных отрезках
получаем:
б) Так как тетраэдр правильный, то все его ребра равны 10.
Так как то
по двум углам.
Запишем отношение подобия и найдем
Так как то
по двум углам.
Запишем отношение подобия и найдем
Так как то имеем:
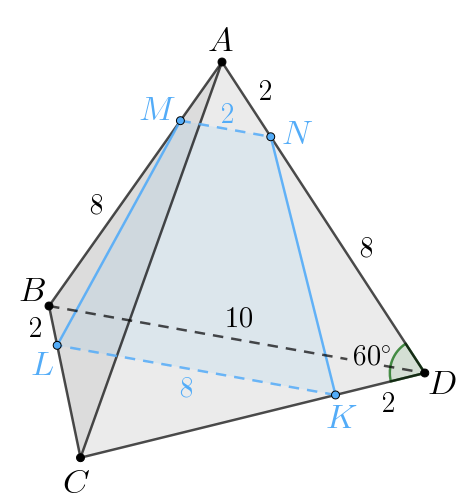
Отметим, что все грани правильного тетраэдра являются равносторонними
треугольниками. Следовательно,
Получаем, что по двум сторонам и углу между ними:
Следовательно, Тогда так как
то сечение
тетраэдра — равнобедренная трапеция с основаниями
и
Найдем боковую сторону трапеции. По теореме косинусов для
Найдем площадь трапеции Для этого проведем высоты
и
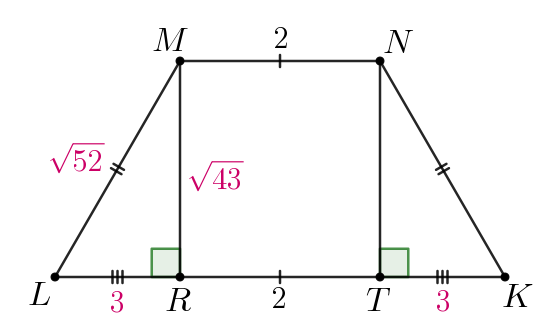
Так как трапеция равнобедренная, то имеем:
Тогда по теореме Пифагора для
Отсюда площадь трапеции равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
На ребрах
и
правильного тетраэдра
отмечены точки
и
соответственно. Известно, что
а) Докажите, что плоскость проходящая через точки
и
делит
ребро
в отношении
считая от вершины
б) Найдите площадь сечения тетраэдра плоскостью
если
Источники:
а) Так как то по обратной теореме о пропорциональных
отрезках
Пусть плоскость сечения пересекает
в точке
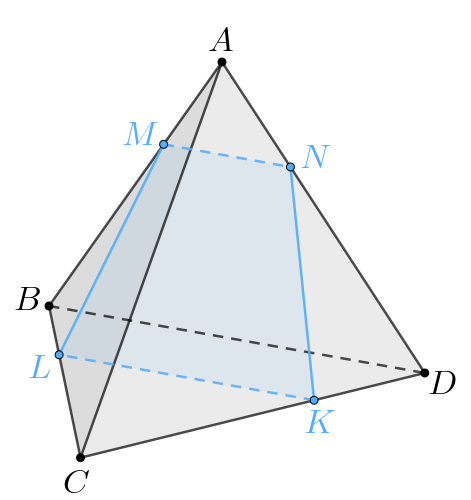
Линии пересечения трех попарно пересекающихся плоскостей либо попарно параллельны, либо пересекаются в одной точке.
Тогда рассмотрим плоскости
и
Они пересекаются
по прямым
и
Так как
то линии пересечения
плоскостей не могут пересекаться в одной точке. Следовательно, они попарно
параллельны:
Отсюда Тогда по теореме о пропорциональных отрезках
получаем:
б) Так как тетраэдр правильный, то все его ребра равны 6.
Так как то
по двум углам.
Запишем отношение подобия:
Так как то
по двум углам.
Запишем отношение подобия:
Так как то имеем:
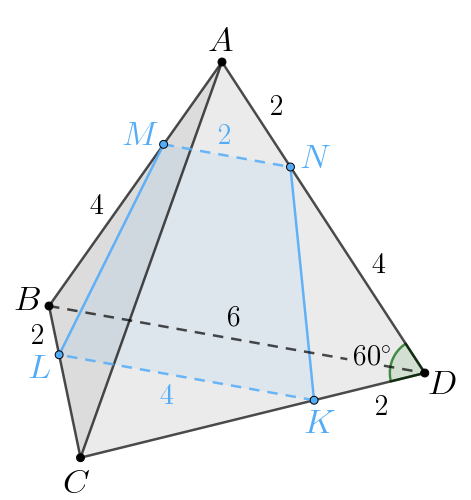
Отметим, что все грани правильного тетраэдра являются равносторонними
треугольниками. Следовательно
Получаем, что по двум сторонам и углу между ними:
Следовательно, Тогда так как
то сечение
тетраэдра — равнобедренная трапеция с основаниями
и
Найдем боковую сторону трапеции. По теореме косинусов для
Найдем площадь трапеции Для этого проведем высоты
и
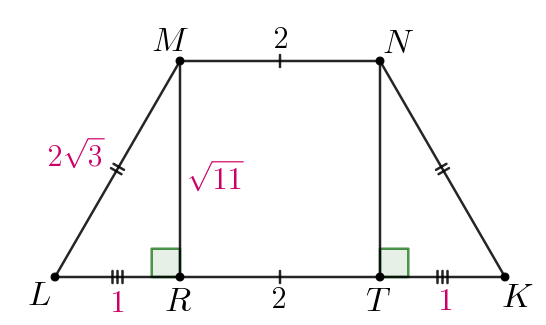
Так как трапеция равнобедренная, то
Тогда по теореме Пифагора для
Отсюда площадь трапеции равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная призма Точка
лежит на ребре
и делит
его в отношении
Точка
— середина ребра
Плоскость
проходит через точки
и
и пересекает ребра
и
в точках
и
соответственно. Известно, что
а) Докажите, что
б) Найдите угол между плоскостью и плоскостью основания призмы, если
все рёбра призмы равны.
Источники:
а) Проведем высоту в основании
Так как призма правильная, то
основания являются равносторонними треугольниками. Следовательно,
также является медианой.
Пусть сторона основания равна Тогда
и так как
то
Отсюда
В треугольнике точка
— середина
точка
— середина
Следовательно,
— средняя линия, то есть
и
Если параллельные плоскости пересекаются третьей плоскостью, то линии
пересечения параллельны. Плоскость пересекает параллельные плоскости
и
по прямым
и
значит,
Так как
то отсюда
Что и требовалось доказать.
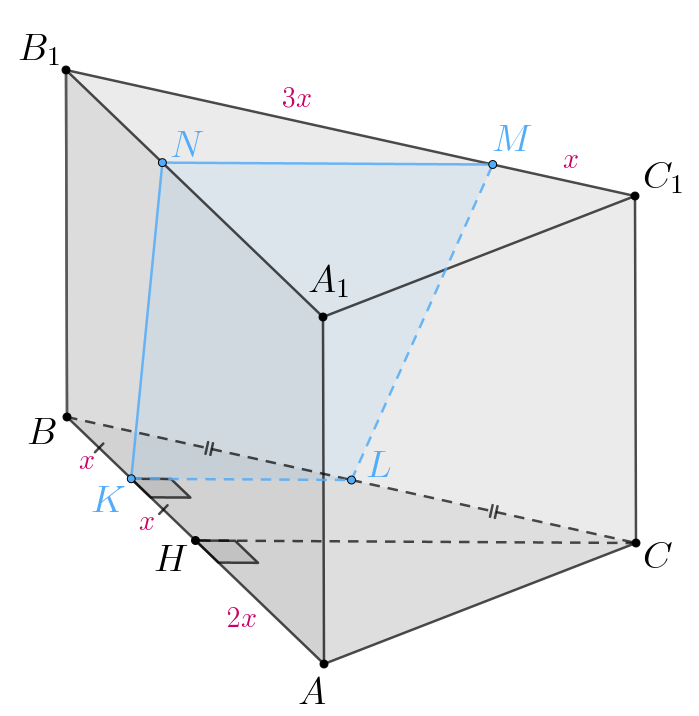
б) Проведем высоту в основании
Так как
то
Тогда
и по теореме о пропорциональных
отрезках имеем:
Так как то
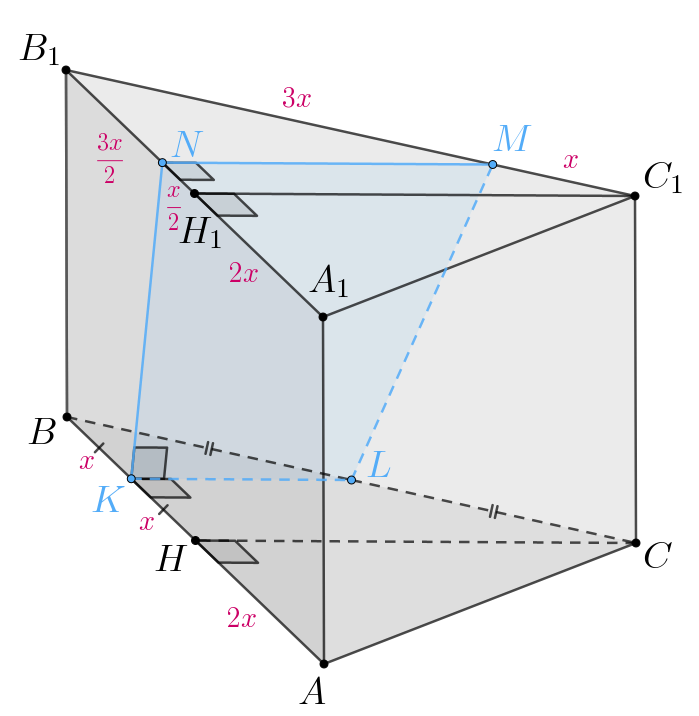
Так как призма правильная, то в частности,
Тогда
следовательно,
Отсюда
Заметим, что — прямая пересечения плоскостей
и
и
Следовательно, угол между данными плоскостями равен углу
Рассмотрим грань Так как по условию все ребра призмы равны, то
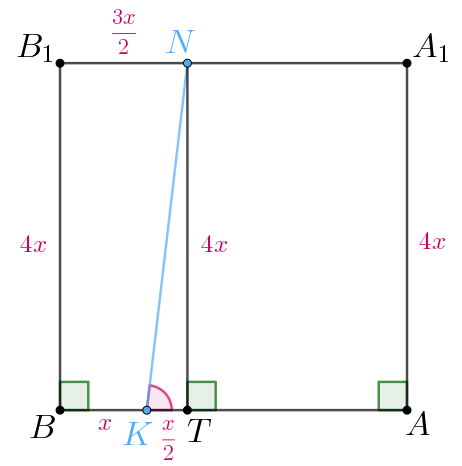
Проведем Тогда
Отсюда
Так как то из прямоугольного треугольника
получаем:
Таким образом, искомый угол между плоскостью и плоскостью основания
призмы равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Плоскость перпендикулярна плоскости основания
правильной
четырёхугольной пирамиды
и пересекает ребро
в точке
Сечение пирамиды плоскостью
является правильным треугольником площадью
а) Докажите, что плоскость перпендикулярна прямой
б) В каком отношении точка делит ребро
считая от точки
если
объём пирамиды равен
Источники:
а) Проведём параллельно
тогда
Здесь
— высота
пирамиды, при этом так как
— правильная, то
— точка пересечения
диагоналей основания
Так как по условию
то прямая
проходящая через точку
и перпендикулярная
лежит в
плоскости
Далее, плоскости и
имеют общую точку
Тогда эти
плоскости пересекаются по некоторой прямой. Пусть это будет прямая
где
— точки пересечения со сторонами
и
основания
соответственно.
Так как перпендикулярна плоскости основания, то
перпендикулярна
Покажем, что
перпендикулярна
- Из свойств квадрата
— биссектриса угла
- Из свойств правильного треугольника
высота
является и медианой, то есть
Тогда — медиана и биссектриса в треугольнике
а значит, является
и высотой. Тогда
то есть
перпендикулярна
плоскости
Что и требовалось доказать.
![]()
б) Распишем объёмы пирамид и
Выразим нужные отношения через Рассмотрим подобные по острому
углу прямоугольные треугольники
и
Запишем отношение подобия:
Найдем отношение площадей:
Из подобия по общему острому углу прямоугольных треугольников и
имеем:
Тогда получаем:
Чтобы найти запишем площадь правильного треугольника
Из
свойств правильного треугольника известно, что
Тогда
имеем:
Отсюда получаем, что
Из прямоугольного равнобедренного треугольника
Отсюда Найдем объем пирамиды
Тогда имеем:
Откуда получаем, что Отсюда если
то
и
Тогда искомое отношение равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде с основанием
известно, что
Через точку
пересечения диагоналей основания
перпендикулярно ребру
провели плоскость
а) Докажите, что плоскость проходит через вершины
и
б) В каком отношении плоскость делит ребро
считая от вершины
если площадь сечения равна
Источники:
а) Прямая перпендикулярна плоскости
если она перпендикулярна двум
пересекающимся прямым из этой плоскости. Поэтому найдем две прямые,
проходящие через точку
и перпендикулярные
Так как пирамида правильная, то — ее высота,
Тогда по
теореме о трех перпендикулярах
Так как
то
Что
и требовалось доказать.
Найдем вторую прямую. Проведем в высоту
то есть
Тогда
— сечение пирамиды плоскостью
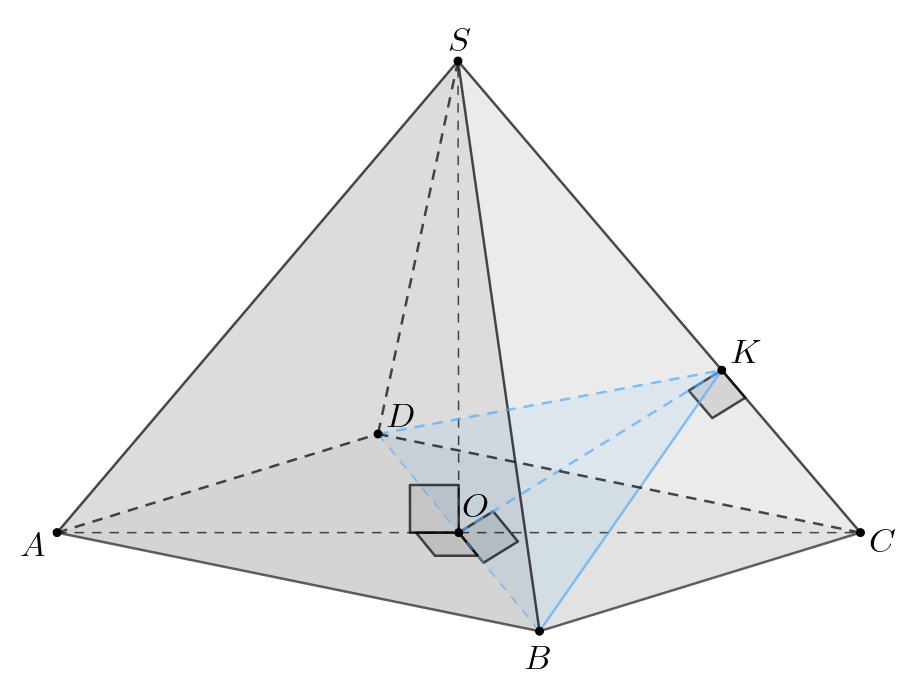
б) Требуется найти
По доказанному в пункте а) имеем:
Следовательно,
Тогда
Следовательно, площадь сечения равна
Так как и
— квадрат, то
Тогда площадь сечения равна
Перейдем в

По теореме Пифагора для треугольника
Найдем через свойство высоты из вершины прямого угла:
Значит, искомое отношение равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде с основанием
известно, что
Через точку
пересечения диагоналей основания
перпендикулярно ребру
провели плоскость
а) Докажите, что плоскость проходит через вершины
и
б) В каком отношении плоскость делит ребро
считая от вершины
если площадь сечения равна
Источники:
а) Прямая перпендикулярна плоскости
если она перпендикулярна двум
пересекающимся прямым из этой плоскости. Поэтому найдем две прямые,
проходящие через точку
и перпендикулярные
Так как пирамида правильная, то — ее высота,
Тогда по
теореме о трех перпендикулярах
Так как
то
Что
и требовалось доказать.
Найдем вторую прямую. Проведем в высоту
то есть
Тогда
— сечение пирамиды плоскостью
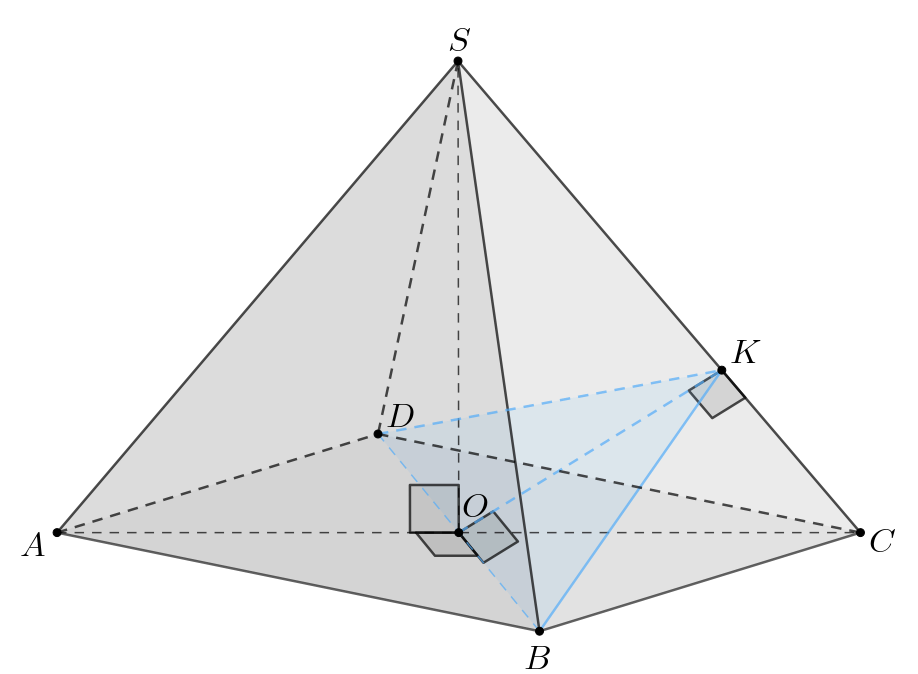
б) Требуется найти
По доказанному в пункте а) имеем:
Следовательно,
Тогда
Следовательно, площадь сечения равна
Так как и
— квадрат, то
Тогда площадь сечения равна
Перейдем в

По теореме Пифагора для треугольника
Найдем через свойство высоты из вершины прямого угла:
Значит, искомое отношение равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная четырехугольная пирамида с основанием
Плоскость
проходит через ребро
и пересекает ребра
и
в точках
и
соответственно. Известно, что
а) Докажите, что
б) Найдите косинус угла между плоскостью и плоскостью основания
пирамиды.
Источники:
а) Рассмотрим три попарно пересекающиеся плоскости:
Прямые
и
— их линии пересечения. Тогда эти прямые либо
пересекаются в одной точке, либо попарно параллельны. Так как
то
имеем:
Тогда
Отсюда следует, что
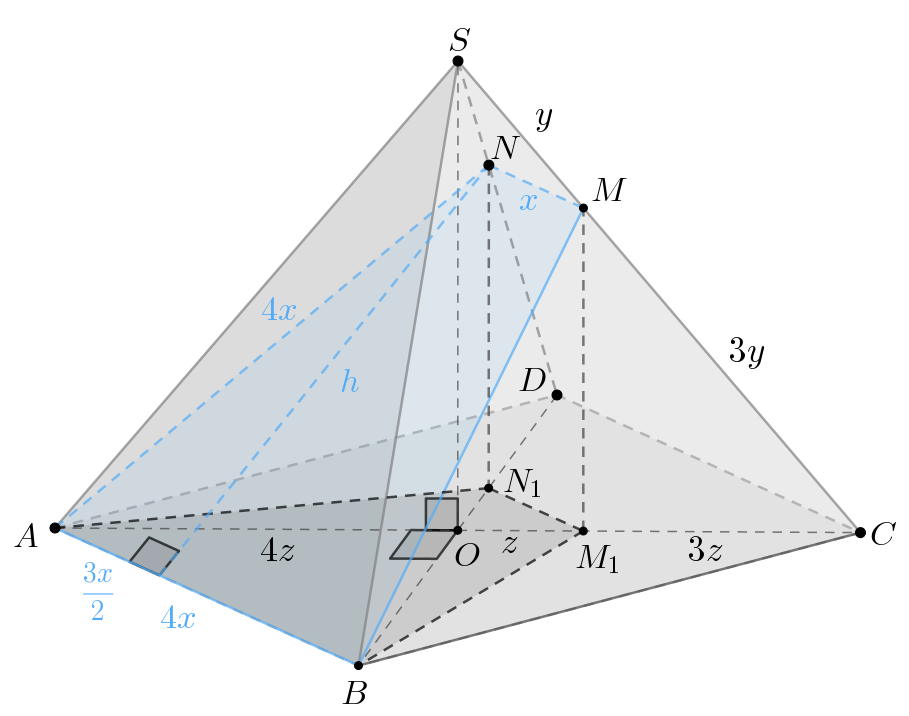
б) Пусть
Пусть — точка пересечения диагоналей
и
Так как пирамида
правильная, то
— высота этой пирамиды.
В плоскости проведем
Тогда
— проекция точки
на
плоскость
В плоскости проведем
Тогда
— проекция точки
на
плоскость
Значит, четырехугольник — проекция сечения
на плоскость
Если — угол между плоскостями
и
то
Рассмотрим Это равнобедренная трапеция. Пусть
— ее высота.
Тогда образуется прямоугольный треугольник с гипотенузой
и катетами
и
Следовательно, по теореме Пифагора:
Значит, площадь сечения равна
По теореме о пропорциональных отрезках
Аналогично
Пусть
Тогда
Диагонали и
четырехугольника
взаимно
перпендикулярны, следовательно, его площадь равна
Но по свойству квадрата
Отсюда площадь проекции сечения равна
Тогда искомый косинус равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная четырехугольная пирамида с основанием
Плоскость
проходит через ребро
и пересекает ребра
и
в точках
и
соответственно. Известно, что
а) Докажите, что
б) Найдите косинус угла между плоскостью и плоскостью основания
пирамиды.
Источники:
а) Рассмотрим три попарно пересекающиеся плоскости:
Прямые
и
— их линии пересечения. Тогда эти прямые либо
пересекаются в одной точке, либо попарно параллельны. Так как
то
имеем:
Тогда
Отсюда следует, что
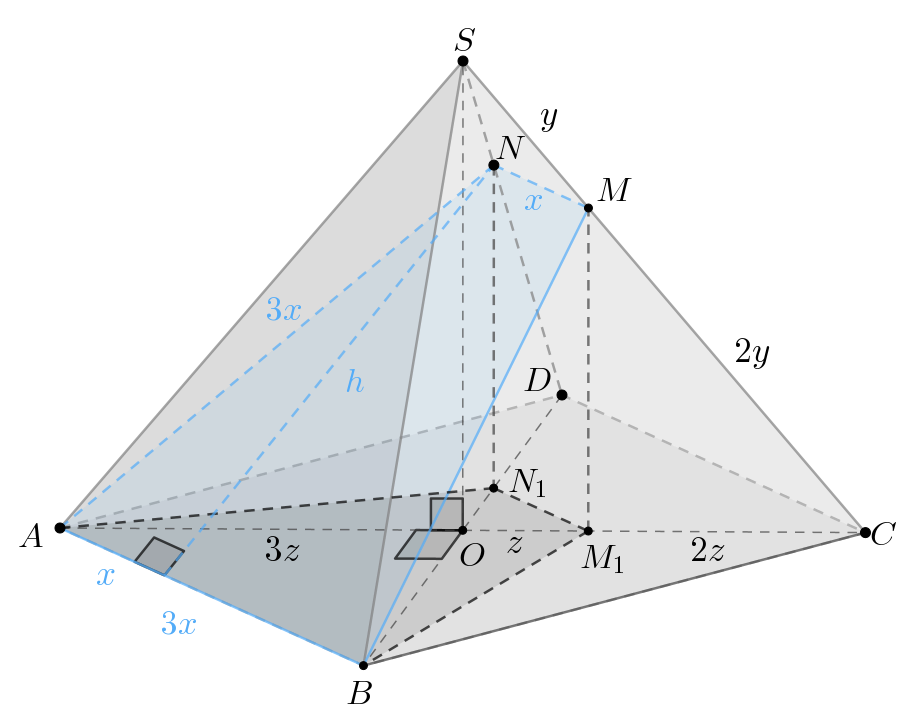
б) Пусть
Пусть — точка пересечения диагоналей
и
Так как пирамида
правильная, то
— высота этой пирамиды.
В плоскости проведем
Тогда
— проекция точки
на
плоскость
В плоскости проведем
Тогда
— проекция точки
на
плоскость
Значит, четырехугольник — проекция сечения
на плоскость
Если — угол между плоскостями
и
то
Рассмотрим Это равнобедренная трапеция. Пусть
— ее высота.
Тогда образуется прямоугольный треугольник с гипотенузой
и катетами
и
Следовательно, по теореме Пифагора:
Значит, площадь сечения равна
По теореме о пропорциональных отрезках
Аналогично
Пусть
Тогда
Диагонали и
четырехугольника
взаимно
перпендикулярны, следовательно, его площадь равна
Но по свойству квадрата
Отсюда площадь проекции сечения равна
Тогда искомый косинус равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме отметили точки
и
на
ребрах
и
соответственно. Известно, что
Через точки
и
провели плоскость
перпендикулярно грани
а) Докажите, что плоскость проходит через вершину
б) Найдите площадь сечения призмы плоскостью
если все
ребра призмы равны 12.
Источники:
а) Так как призма правильная, то — равносторонний треугольник.
Следовательно, медиана
является также и высотой треугольника
.
Отсюда
Также так как призма правильная, то
Получили, что перпендикулярна двум пересекающимся прямым из
плоскости
следовательно,
Так как
и
то
Что и
требовалось доказать.
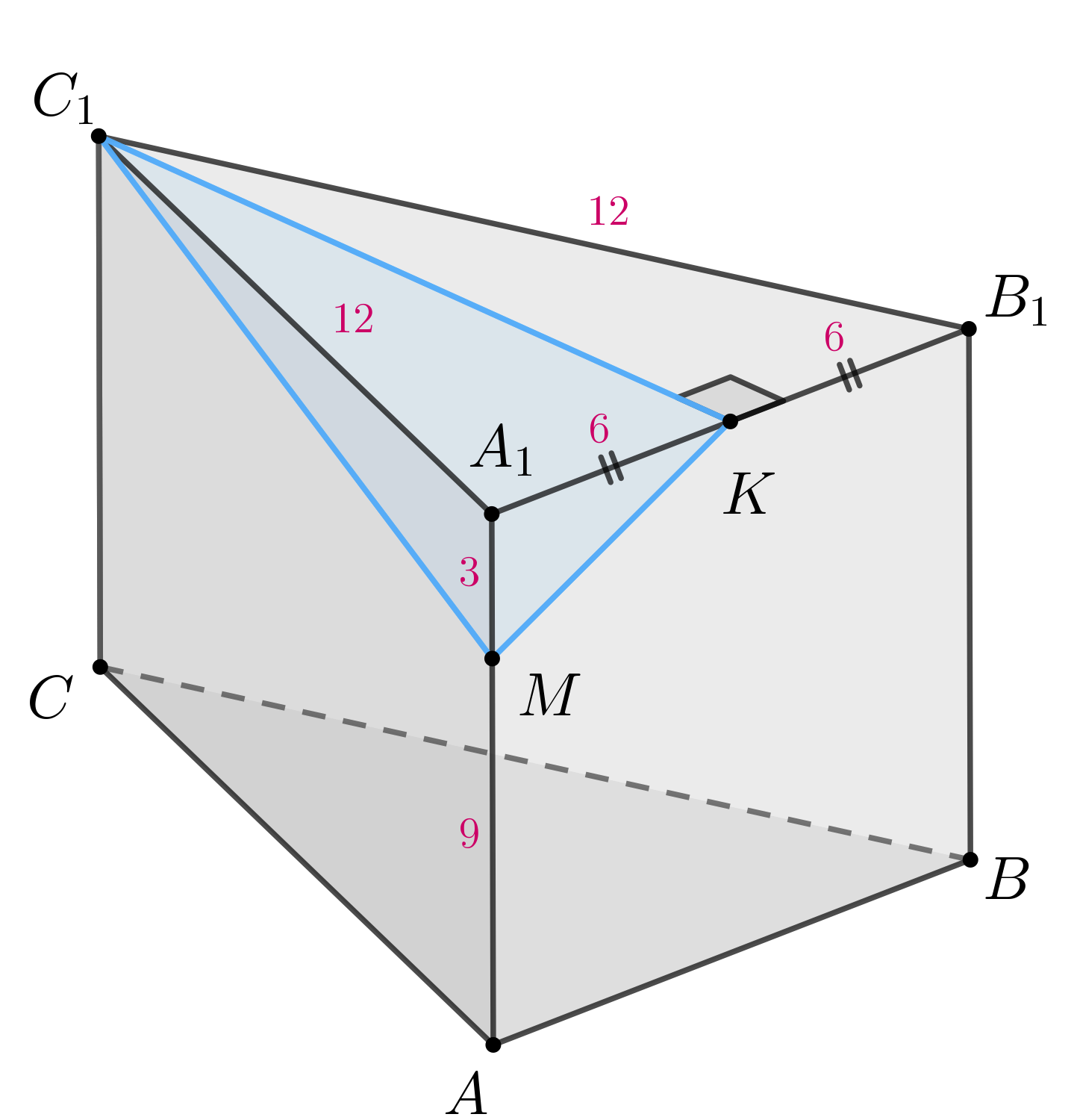
б) Выше мы доказали, что Но тогда
следовательно,
— прямоугольный треугольник и его площадь можно найти
по формуле:
Так как все ребра призмы равны 12, то Далее, из того, что
получаем
Тогда по теореме Пифагора для
По теореме Пифагора для
Тогда искомая площадь равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Плоскость перпендикулярна плоскости основания
правильной
четырёхугольной пирамиды
и пересекает ребро
в точке
Сечение пирамиды плоскостью
является правильным треугольником площадью
а) Докажите, что плоскость перпендикулярна прямой
б) В каком отношении точка делит ребро
считая от точки
если
объём пирамиды равен
Источники:
а) Проведём параллельно
тогда
Здесь
— высота
пирамиды, при этом так как
— правильная, то
— точка пересечения
диагоналей основания
Так как по условию
то прямая
проходящая через точку
и перпендикулярная
лежит в
плоскости
Далее, плоскости и
имеют общую точку
Тогда эти
плоскости пересекаются по некоторой прямой. Пусть это будет прямая
где
— точки пересечения со сторонами
и
основания
соответственно.
Так как перпендикулярна плоскости основания, то
перпендикулярна
Покажем, что
перпендикулярна
- Из свойств квадрата
— биссектриса угла
- Из свойств правильного треугольника
высота
является и медианой, то есть
Тогда — медиана и биссектриса в треугольнике
а значит, является
и высотой. Тогда
то есть
перпендикулярна
плоскости
Что и требовалось доказать.
![]()
б) Распишем объёмы пирамид и
Выразим нужные отношения через Рассмотрим подобные по острому
углу прямоугольные треугольники
и
Запишем отношение подобия:
Найдем отношение площадей:
Из подобия по общему острому углу прямоугольных треугольников и
имеем:
Тогда получаем:
Чтобы найти запишем площадь правильного треугольника
Из
свойств правильного треугольника известно, что
Тогда
имеем:
Отсюда получаем, что
Из прямоугольного равнобедренного треугольника
Отсюда Найдем объем пирамиды
Тогда имеем:
Откуда получаем, что Отсюда если
то
и
Тогда искомое отношение равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
На ребрах
и
правильного тетраэдра
отмечены точки
и
соответственно. Известно, что
а) Докажите, что плоскость проходящая через точки
и
делит
ребро
в отношении
считая от вершины
б) Найдите площадь сечения тетраэдра плоскостью
если
Источники:
а) Так как то по обратной теореме о пропорциональных
отрезках
Пусть плоскость сечения пересекает
в точке
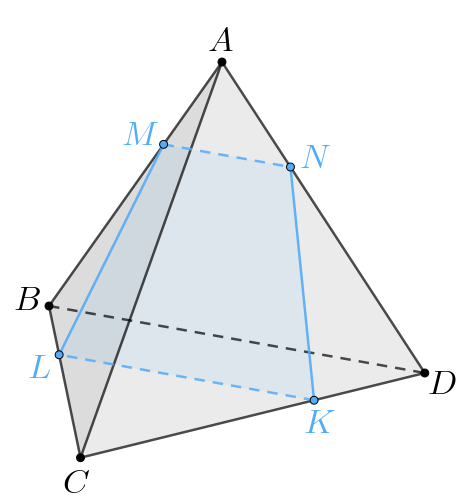
Линии пересечения трех попарно пересекающихся плоскостей либо попарно параллельны, либо пересекаются в одной точке.
Тогда рассмотрим плоскости
и
Они пересекаются
по прямым
и
Так как
то линии пересечения этих
плоскостей не могут пересекаться в одной точке. Следовательно, они попарно
параллельны:
Отсюда Тогда по теореме о пропорциональных отрезках
получаем:
б) Так как тетраэдр правильный, то все его ребра равны 8.
Так как то
по двум углам.
Запишем отношение подобия и найдем
Так как то
по двум углам.
Запишем отношение подобия и найдем
Так как то имеем:
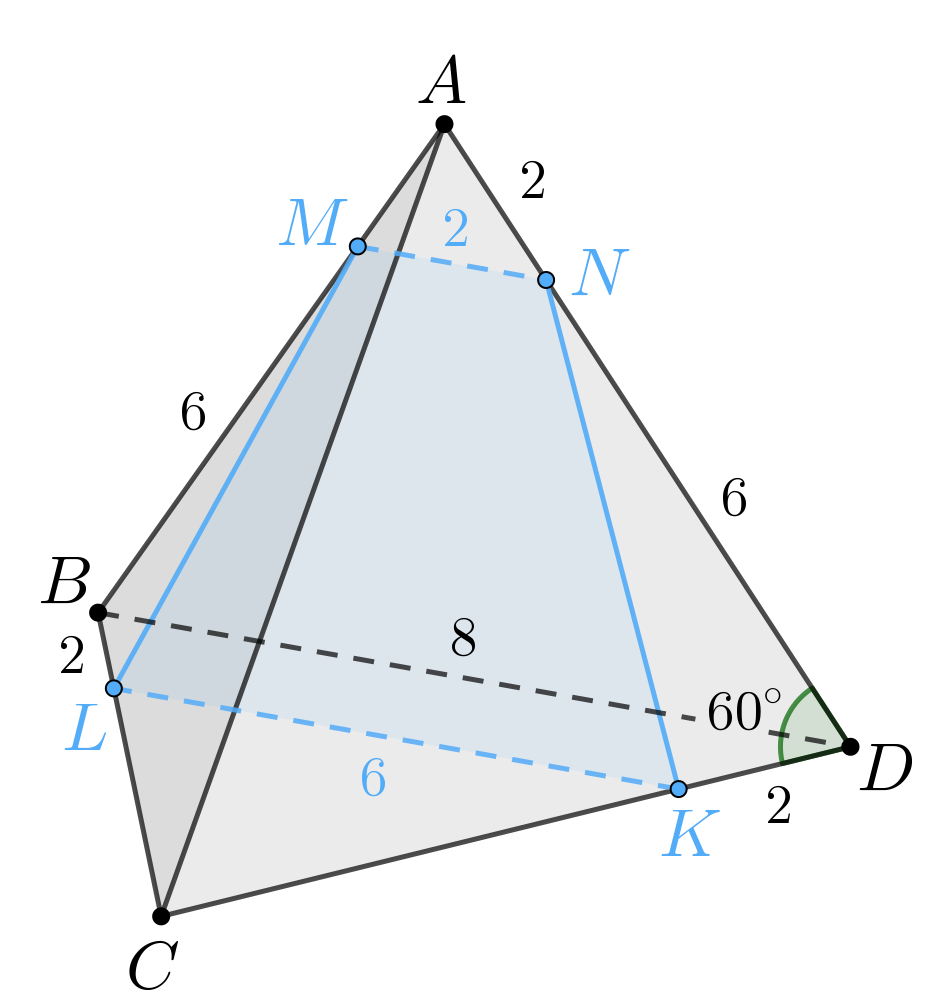
Отметим, что все грани правильного тетраэдра являются равносторонними
треугольниками. Следовательно,
Получаем, что по двум сторонам и углу между ними:
Следовательно, Тогда так как
то сечение
тетраэдра — равнобедренная трапеция с основаниями
и
Найдем боковую сторону трапеции. По теореме косинусов для
Найдем площадь трапеции Для этого проведем высоты
и
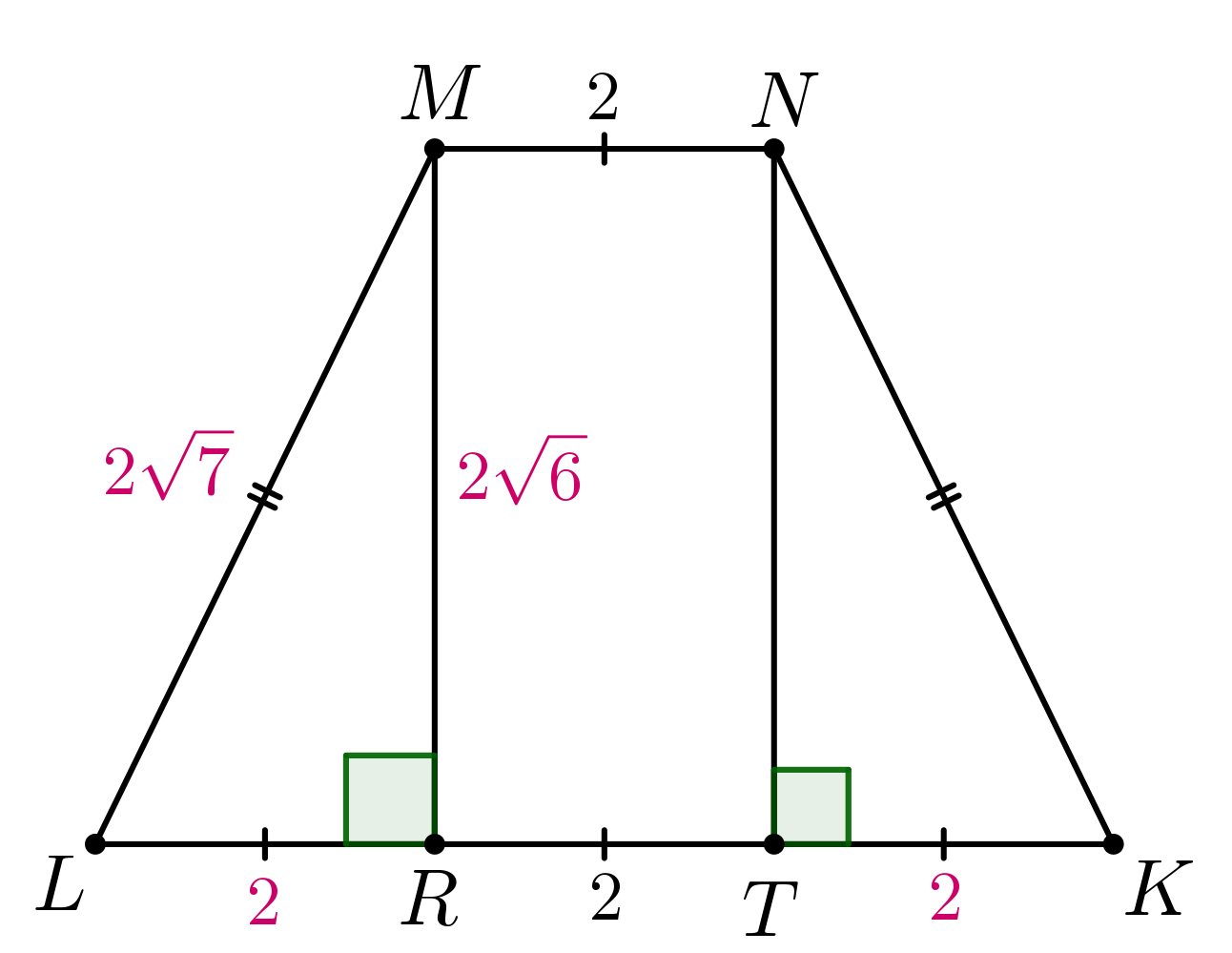
Так как трапеция равнобедренная, то имеем:
Тогда по теореме Пифагора для
Отсюда площадь трапеции равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная призма точка
— середина ребра
Плоскость
проходит через точки
и
а) Докажите, что сечение призмы плоскостью является равнобедренным
треугольником.
б) Найдите высоту призмы, если площадь сечения призмы плоскостью равна
18 и
Источники:
а) Рассмотрим прямоугольные треугольники и
Их катеты
и
равны, так как
— середина
по условию. Также равны
катеты
и
поскольку призма правильная, то есть оба треугольника в
основании правильные с равными сторонами.
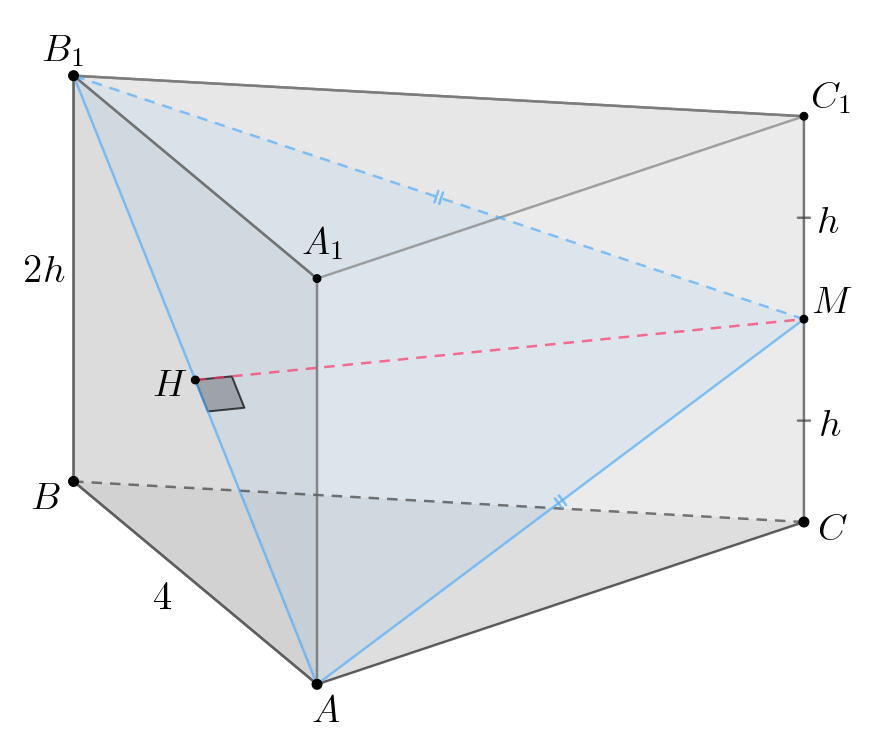
Тогда по двум катетам. Тогда равны их гипотенузы
То есть треугольник
— равнобедренный, что и требовалось
доказать.
б) Пусть Тогда
- по теореме Пифагора
Поскольку треугольник — равнобедренный с основанием
то
его высота
делит сторону
пополам. То есть
.
Вновь воспользуемся теоремой Пифагора:
Теперь запишем площадь сечения:
По условию имеем:
Тогда высота призмы равняется то есть
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная призма точка
— середина ребра
Плоскость
проходит через точки
и
а) Докажите, что сечение призмы плоскостью является равнобедренным
треугольником.
б) Найдите высоту призмы, если площадь сечения призмы плоскостью равна
6 и
Источники:
а) Рассмотрим прямоугольные треугольники и
Их катеты
и
равны, так как
— середина
по условию. Также равны
катеты
и
поскольку призма правильная, то есть оба треугольника в
основании правильные с равными сторонами.
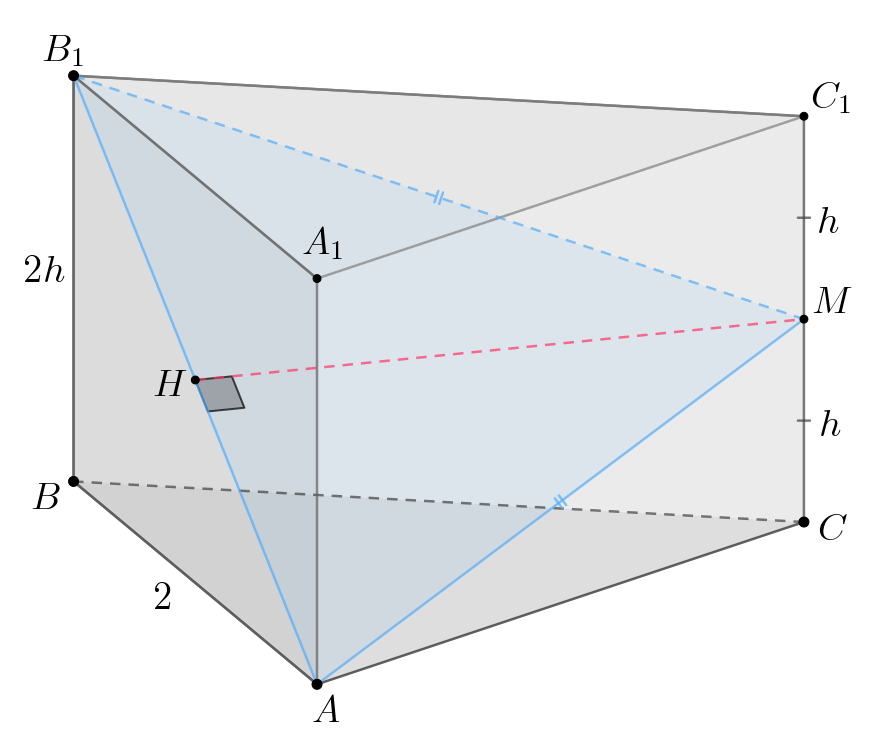
Тогда по двум катетам. Тогда равны их гипотенузы
То есть треугольник
— равнобедренный, что и требовалось
доказать.
б) Пусть Тогда
- по теореме Пифагора
Поскольку треугольник — равнобедренный с основанием
то
его высота
делит сторону
пополам. То есть
Вновь воспользуемся теоремой Пифагора:
Теперь запишем площадь сечения:
По условию имеем:
Высота призмы равняется то есть
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
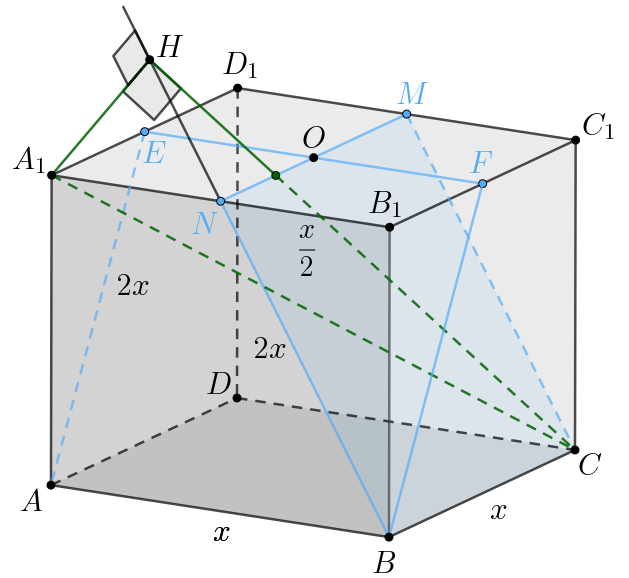
Дан прямоугольный параллелепипед Точка
— центр грани
Сечения параллелепипеда плоскостями
и
являются
прямоугольниками,
и
— их меньшие стороны соответственно.
Известно, что
и
в 2 раза меньше соответственных больших сторон
прямоугольников.
а) Докажите, что — квадрат.
б) Найдите угол между прямой и плоскостью
Источники:
а) Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны.
Тогда плоскость пересекает плоскость верхнего основания по прямой,
параллельной
Пусть данная прямая пересекает
и
в точках
и
соответственно.
Плоскость пересекает плоскость верхнего основания по прямой,
параллельной
Пусть данная прямая пересекает
и
в точках
и
соответственно.
Пусть
Тогда по условию
Так как и
проходят через центр
прямоугольника
то имеем:
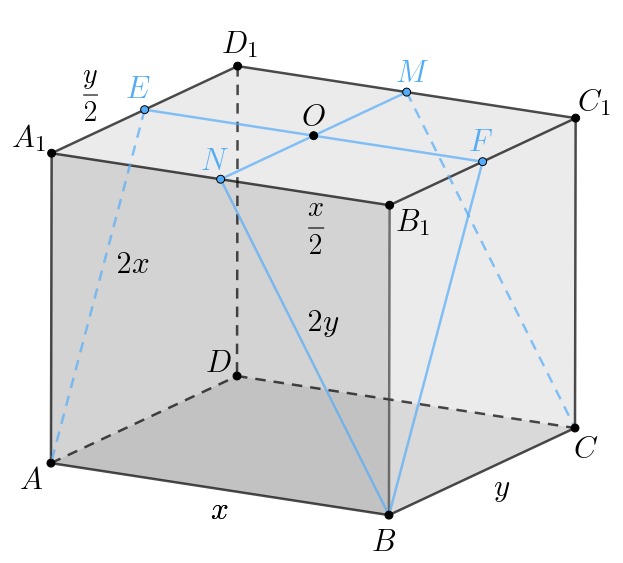
Так как — прямоугольный параллелепипед, то его
боковые ребра перпендикулярны основаниям. Тогда по теореме Пифагора для
прямоугольного треугольника
По теореме Пифагора для прямоугольного треугольника
Так как то получаем уравнение:
Получили, что значит,
— прямоугольник с равными
сторонами, то есть квадрат.
б) Опустим перпендикуляр на продолжение
за точку
Так как
и точка
лежат в плоскости
то
также лежит в данной
плоскости.
Заметим, что то есть
Также
так как
Тогда прямая
перпендикулярна двум пересекающимся
прямым из плоскости
следовательно,
Тогда
перпендикулярна любой прямой из плоскости
в частности
Получили, что
следовательно,
То
есть
— проекция точки
на плоскость
тогда угол между прямой
и плоскостью
равен углу
Найдем его из прямоугольного
треугольника
Найдем Из пункта а) имеем:
по двум углам:
как вертикальные,
Запишем отношение подобия:
По формуле диагонали прямоугольного параллелепипеда:
Тогда из прямоугольного треугольника имеем:
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |



