Тема ММО - задания по годам

ММО 2015

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела ммо - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#31504

В прошлом году Миша купил смартфон, который стоил целое четырёхзначное число рублей. Зайдя в магазин в этом году, он заметил, что цена смартфона выросла на $20%$ и при этом состоит из тех же цифр, но в обратном порядке. Какую сумму Миша потратил на смартфон?

Источники: ММО-2015, 11.2, автор - М.А.Евдокимов. (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Обозначьте первоначальную стоимость смартфона переменной и попробуйте порассуждать о делимости. Числа а и 1.2а — целые, что можно о них сказать?

Подсказка 2

Попробуйте дальше порассуждать о числах, которые задают стоимость смартфона: какой может быть последняя цифра такого числа? А в каких пределах лежит эта цена?

Подсказка 3

Внимательные рассуждения по первым двум пунктам должны были помочь вам установить первую и последнюю цифру нашей цены. Самое время записать наши цены в десятичной форме!Помните, их разность тоже должна быть целой — может быть и её выразим?

Подсказка 4

Теперь мы можем сделать вывод о двух оставшихся числах и их делимости на 9. Остался лишь небольшой перебор и задача решена!

Показать ответ и решение

Пусть изначальная сумма была равна $a$ . Значит число $1.2a$ и $0.2a$ целое. Отсюда $a= 0.2a⋅5$ делится на 5. Если последняя цифра числа $a$ равна 0, то число $1.2a$ не более чем трехзначное?! Значит, последняя цифра $a$ равно 5. Тогда $6000> 1.2a≥ 5000$ и $5000> a> 4000$ и поэтому первая цифра $a$ равна 4.

Если $a= 4000+ 100a2+ 10a3 +5$ , то $1,2a =5000+100a3+ 10a2+ 4$ и $0,2a= 999+ 90a2− 90a3 = 999 +90(a2− a3)$ . Раз $a= 0.2a⋅5$ , то оно делится на 9. Сумма первой и последней цифры делится на 9. Значит, нам нужно перебрать все целые четырехзначные числа с первой цифрой 4, последней 5 и делящиеся на 9. Значит, они должны давать остаток 45 при делении на 90. Значит, нам нужно постепенно увеличивать на 90 число 4095.

$a =4095$ . Тогда $1.2a= 4914$ ?!
$a =4185$ . Тогда $1.2a= 5022$ ?!
$a =4275$ . Тогда $1.2a= 5130$ ?!

Заметим, что когда $a$ увеличивается на 90, то $1.2a$ увеличивается на 108. При этом мы хотим, чтобы у числа $1.2a$ последняя цифра была 4. Значит, нам на самом деле нужно число 4095 увеличивать на 450 (чтобы последняя цифра у $1.2a$ оставалась 4).

$a =4095$ . Тогда $1.2a= 4914$ ?!
$a =4545$ . Тогда $1.2a= 5454$ и этот вариант подходит.
$a =4995$ . Тогда $1.2a= 5994$ и этот вариант подходит.

Ответ:

$4545$ или $4995$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#40087

Последовательность $(a ) n$ такова, что $a = n2 n$ при $1≤ n ≤5$ и при всех натуральных $n$ выполнено равенство $a +a = a + a . n+5 n+1 n+4 n$ Найдите $a2015.$

Источники: ММО-2015, 11.1, автор - С.Б.Гашков, (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1!

Какие-то странные условия, попробуем получить из них что-то хорошее. Если вы знаете что-то про начальные члены последовательности, а еще про то, как они соотносятся с предыдущими, здорово бы было как-то выразить большие члены через члены от 1 до 5. Получить на них какое-то правило.

Подсказка 2!

Давайте напишем. a(n+5) +a(n+1) = a(n+4) + a(n). Заметим, что индексы в обеих частях отличаются на 4. Напишем a6+a2 = a5+a1 = чему-то, что мы уже знаем! Так, а может не только для а6+а2 мы знаем это равенство?

Подсказка 3!

Да, для всех чисел, отличающихся на 4 по номеру, мы поняли их сумму. Теперь вспомним, что мы ищем 2015. К сожалению, 2019 или 2011 мы не знаем. Попробуем получить еще что-то из условия с равенством. Попробуйте сделать так, чтобы и в левой, и в правой части оказалось одинаковое число.

Подсказка 4!

Да, подставим а(n+8) + а(n+4) = a(n+4)+an. Осталось сделать выводы и применить наши полученные знания :)

Показать ответ и решение

Из условия следует

2 2 an+4+ an = an+3 +an−1 = ...= a6+ a2 =a5 +a1 = 5 + 1 =26

А также

an+8+ an+4 =an+4+ an =⇒ an+8 = an

То есть значение $an$ зависит только от остатка $n$ по модулю $8,$ отсюда

a2015 =a7 = 26− a3 = 26 − 32 = 17

Ответ:

$17$

Ошибка.
Попробуйте повторить позже

Задача 3#89596

Внутри параллелограмма $ABCD$ отметили точку $E$ так, что $CD = CE.$ Докажите, что прямая $DE$ перпендикулярна прямой, проходящей через середины отрезков $AE$ и $BC.$

Подсказки к задаче

Подсказка 1

Непонятно, как на картинке считать углы, а доказать нужно перпендикулярность. Может быть, будем доказывать какой-то эквивалентный факт?

Подсказка 2

Рассмотрим середину DE, треугольник ECD - равнобедренный, а, значит, отрезок CT перпендикулярен DE.

Подсказка 3

Обозначим за M и N середины AE и BC, итак доказываем параллельность СТ и MN. У нас три середины отрезков на картинке отмечено, надо этим воспользоваться.

Показать доказательство

Обозначим середины $AE, BC$ и $DE$ за $M,N$ и $T,$ необходимо доказать перпендикулярность $DE$ и $MN.$ $DE−$ основание равнобедренного треугольника $DEC,$ тогда его медиана $CT$ является также его высотой. Тогда нам достаточно доказать параллельность $MN$ и $T C.$

$MT$ — средняя линия треугольника $AED,$ то есть равна половине $AD$ и параллельна ему. В свою очередь $NC$ равен половине $BC = AD$ и параллелен $AD,$ а значит $MT$ и $NC$ параллельны и равны по длине, значит $MNCT$ — параллелограмм. А значит $MN$ и $TC$ параллельны.

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 4#91094

Будем называть натуральное число почти квадратом, если это либо точный квадрат, либо точный квадрат, умноженный на простое число. Могут ли $8$ почти квадратов идти подряд?

Подсказки к задаче

Подсказка 1

Вам дано 8 последовательных чисел. Подумайте, почему именно 8, а не меньше.

Подсказка 2

Это сделано для того, чтобы они имели разные остатки при делении на 8. Рассмотрите числа 8k, 8k + 1, ..., 8k + 7 в контексте условия задачи.

Подсказка 3

Давайте посмотрим на число 8k + 2. Что вы видите? Конечно, оно делится на 2, но не делится на 4. А что это значит? А про другие числа что можно сказать?

Показать ответ и решение

Cреди восьми последовательных натуральных чисел найдутся числа, дающие остатки $2$ и $6$ при делении на $8.$ Они делятся на $2,$ но не делятся на $4,$ так что они обязаны иметь вид $2 2k$ и $2 2m .$ Тогда $2 2 2k − 2m = 4,$ то есть $2 2 k − m = 2,$ что невозможно. Противоречие.

Ответ:

нет

Ошибка.
Попробуйте повторить позже

Задача 5#106838

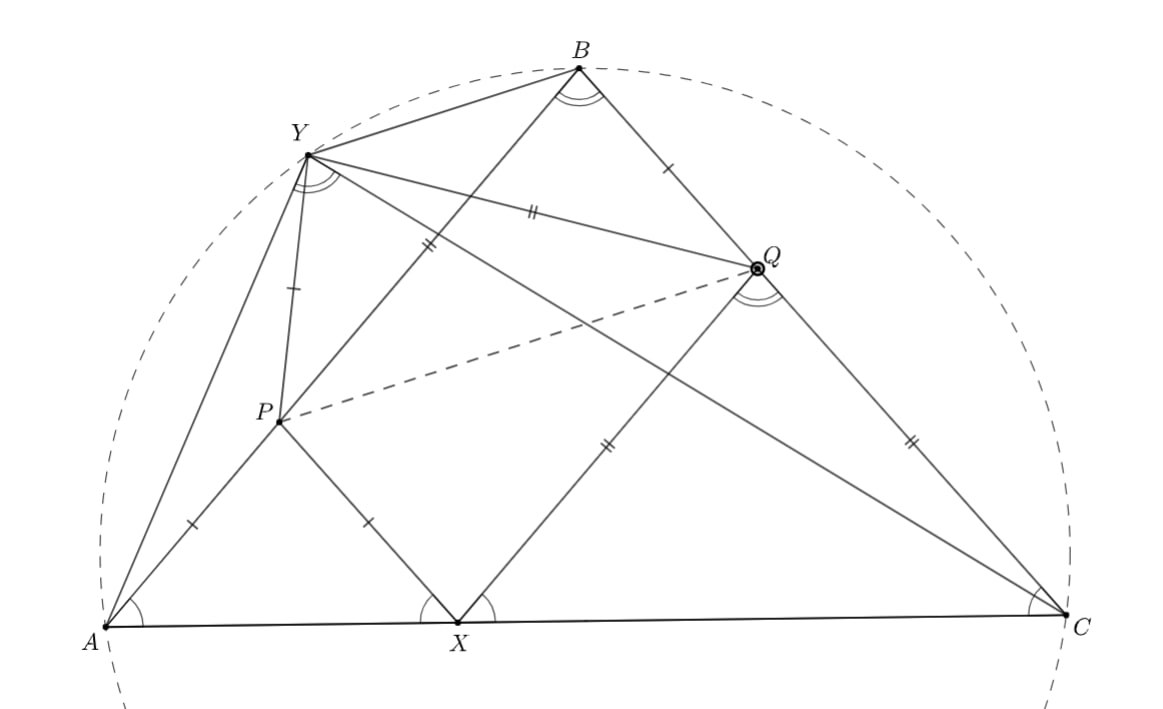
На основании $AC$ равнобедренного треугольника $ABC$ взяли произвольную точку $X,$ а на боковых сторонах — точки $P$ и $Q$ так, что $XP BQ$ — параллелограмм. Докажите, что точка $Y,$ симметричная точке $X$ относительно $PQ,$ лежит на описанной окружности треугольника $ABC.$