Изумруд 2025
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Трёхзначное число состоит из цифр и обладает следующими свойствами:
цифра в разряде единиц равна последней цифре числа
цифра в разряде десятков равна последней цифре числа
цифра в разряде сотен равна последней цифре числа
Найдите все такие числа.
Источники:
Подсказка 1
Обратите внимание, что последняя цифра суммы а + b + с равна с. Это означает, что а + b должно быть кратно 10. Какие пары цифр а и от 1 до 9 дают в сумме 10?
Подсказка 2
Как можно переписать условие "ab + bc + са оканчивается на b"? Попробуйте выразить это через а, b и с, со старыми ограничениями. Какие новые ограничения на с это накладывает?
Подсказка 3
Финишная прямая! Рассмотрите два основных варианта: Если b = 5, то а = 5. Какие с подойдут? Если а = 1, то b = 9. Какое с даст abc, оканчивающееся на 1? Не забудьте проверить а = 6, b = 4.
Заметим, что можно, не умаляя общности, считать, что наше трёхзначное число — это именно так как числа
— симметричные выражения относительно
. Тогда по условию
равно последней цифре числа
но тогда
так как разряд единиц обнулился, то есть
где
так как
Но
значит,
откуда
, то есть
и
Аналогично, так как последняя цифра числа совпадает с
то
Перепишем иначе:
где Тогда
то есть При этом
значит, либо
, либо
(так мы
обеспечим делимость на
Разберём случаи:
- 1.
-
— противоречие.
- 2.
-
Если
то
оканчивается на
то есть
— противоречие. Значит
Заметим, что все эти числа подходят, так как
то заканчивается на
тоже заканчивается на
- 3.
-
Знаем, что последняя цифра числа
равна
то есть
заканчивается на
при этом
а наименьшее натуральное число, кратное
и оканчивающееся на
— это
То есть
— подходит.
- 4.
-
Знаем, что последняя цифра числа
равна
тогда
- 4.1.
-
— подходит.
- 4.2.
-
— подходит.
Итого, ответ:
Ошибка.
Попробуйте повторить позже
В шахматном турнире, состоящем из нескольких туров, приняли участие шахматистов. Перед каждым туром всех игроков случайным
образом делят на
пары, определяя тем самым каждому из шахматистов его противника в этом туре. При этом шахматисты, уже
сыгравшие друг с другом ранее, обязательно распределяются в разные пары. Может ли случиться так, что после проведённых
туров
будет невозможным провести шестой?
Источники:
Подсказка 1
Ответ в задаче — может. Попробуйте придумать пример.
Подсказка 2
Чтобы пример придумывать было проще, попробуйте интерпретировать распределение в раундах в виде некоторой таблицы.
Подсказка 3
Рассмотрим следующую таблицу. Верхняя левая клетка пустая, в левом столбце и верхней строке цифры от 1 до 8 — игроки. Если игроки i и j играли в раунде k, то тогда в клетку (i, j) поставим k. Попробуйте как-то расставить первые 5 раундов, чтобы с помощью небольшого перебора можно было показать, что шестой невозможен.
Рассмотрим табличку Пронумеруем строки и столбцы слева направо и сверху вниз от
до
соответственно.
— клетка на
пересечении
ой строки и
го столбца. В клетку
где
ставим число
если пара
ый шахматист и
ый сыграли в
ом раунде. В клетках
стоят крестики (эти клетки нам не нужны). Клетки, которые ниже диагонали нам не нужны (их оставим
пустыми).
Приведём пример разбиения на пары для первых -ти раундов.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | X | 1 | 2 | 3 | 4 | 5 | |||
| 2 | X | 5 | 1 | 2 | 3 | 4 | |||
| 3 | X | 3 | 2 | 4 | |||||
| 4 | X | 4 | 5 | ||||||
| 5 | X | 5 | 1 | ||||||
| 6 | X | 1 | 2 | ||||||
| 7 | X | 3 | |||||||
| 8 | X | ||||||||
Докажем, что раунд провести нельзя.
-ый сыграл со всеми, кроме
-го и
-го. В клетки, пары которых выбрать на
-м ходе
нельзя, будем писать No. Разберём два случая:
- 1.
-
-ый сыграл со
-ым. Тогда имеем следующую ситуацию:
1 2 3 4 5 6 7 8 1 X 6 1 2 3 4 5 No 2 X 5 1 2 3 4 No 3 X 3 2 4 4 X 4 5 5 X 5 1 6 X 1 2 7 X 3 8 X Осталось расставить
шестёрки. Все они стоят в разных столбцах и разных строках. Но столбцов, где есть свободные клетки всего
значит, в каждом из них ровно по одной шестёрке, тогда в клетке
обязательно есть
Но тогда в клетке
точно нет шестёрки, и в столбце
всего
свободных клетки, значит, в
точно шестёрка, но тогда в
её нет, значит, она есть в
так как в столбце
всего
свободных. Итого, есть шестёрка в
и в
— противоречие, так как
-ый сыграл дважды за
раунд.
1 2 3 4 5 6 7 8 1 X 6 1 2 3 4 5 No 2 X 5 1 2 3 4 No 3 X 3 6 No 2 4 4 X 4 6 No 5 5 X 5 6 1 6 X 1 2 7 X 3 8 X - 2.
-
-ый сыграл с
-ым. Тогда имеем следующую ситуацию:
1 2 3 4 5 6 7 8 1 X No 1 2 3 4 5 6 2 X 5 1 2 3 4 No 3 X 3 2 4 4 X 4 5 5 X 5 1 6 X 1 2 7 X 3 8 X Далее аналогичными рассуждениями из предыдущего пункта получаем противоречие.
В обоих случаях противоречие, следовательно, пример рабочий.
Может
Ошибка.
Попробуйте повторить позже
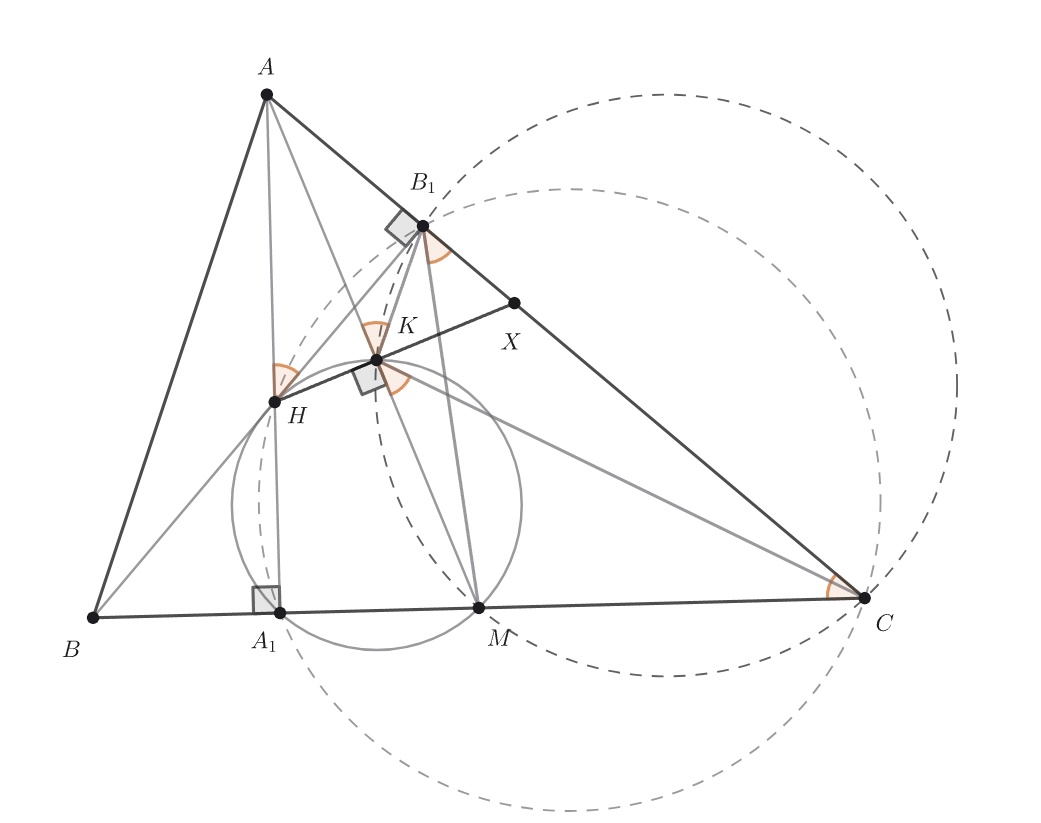
Высоты и
остроугольного неравнобедренного треугольника
пересекаются в точке
Точка
— середина стороны
Описанная окружность треугольника
пересекает отрезок
в точке
Докажите, что
— биссектриса угла
Источники:
Подсказка 1
Если в контексте задачи фигурирует ортоцентр, то на картинке скорее всего будет много вписанных четырёхугольников и эта задача — не исключение.
Подсказка 2:
Обратите внимание на четырёхугольники MKB₁C и A₁HB₁C, а также на степень точки A относительно соответствующих окружностей и найдите ещё вписанные четырёхугольники.
Подсказка 3:
Если вы всё сделали верно, то четырёхугольники MKB₁C, A₁HB₁C, A₁HKM, AHKB₁ должны быть вписанными. Для завершения решения поперекидывайте угол ACB в окружностях.
Так как — высота, то
Аналогично
Тогда
— вписанный четырёхугольник, так как
Степень точки
относительно окружности
с одной стороны равна
с другой —
То есть
тогда
— вписанный, и аналогично из степени точки
получаем, что
Итого,
то есть — вписанный.
Так как и
— смежные углы и
— вписанный, то
откуда
Так как
— вписанный, то
из-за того, что и
— смежные углы. А также получаем:
Отсюда — вписанный, тогда
Из вписанности знаем, что
а из смежности знаем, что
Тогда
В треугольнике
и точка
— середина гипотенузы, значит,
то есть треугольник
—
равнобедренный, тогда:
Так как — вписанный, то
Тогда получаем, что:
— вписанный, тогда
так как
То есть
значит,
где
Получаем:
то есть значит,
— биссектриса
Что и требовалось доказать.
Ошибка.
Попробуйте повторить позже
Найдите все тройки натуральных чисел являющиеся решением уравнения
Источники:
Подсказка 1
Обратите внимание, число 2^{xy} почти всегда значительно больше числа 2^{x + y}. Попробуйте формализовать эту идею.
Подсказка 2
Пусть x, y ≥ 6. Давайте зафиксируем y, выразим z через x и y. Осталось показать, что при больших х это выражение будет меньше 1, значит, решений не будет.
Подсказка 3
Доказывать стоит по индукции. Глобальная идея — показать, что знаменатель выражения увеличивается в большее количество раз, чем числитель при увеличении x.
Задача симметрична относительно и
Пусть
Тогда
или
чего не бывает. Значит,
Аналогично,
Пусть
Тогда
или
Тогда получаем решения при
при
при
При
по индукции покажем, что
то есть решений нет. База при
верна. Рассмотрим
следующие оценки числителя и знаменателя в переходе
и
то есть числитель увеличился
менее, чем вдвое, а знаменатель более, чем вдвое, значит,
уменьшилось. Теперь можно считать, что
Тогда
Пусть
Тогда
то есть равенства нет. Тогда и
Покажем, что при
Снова используем индукцию: пусть
Тогда при
получаем
Теперь
переход индукции:
что и требовалось. Оценим левую часть, используя полученное неравенство:
Далее то есть
Тогда в левой части
Пусть
Тогда
по прошлой оценке, то есть равенство возможно только при Теперь пусть
или
хотя бы
Тогда
и
что снова противоречит оценке правой части. Значит, Подставляя тройку
понимаем, что это не будет решением.
Итого, мы получили ответ из шести троек (учитывая то, что есть симметричные для
и
и
Ошибка.
Попробуйте повторить позже
Есть доска размера разделённая на единичные квадраты. Витя хочет выбрать
из этих единичных квадратов со следующим
свойством: никакие два квадрата не находятся в одной строке или в одном столбце, и ни у каких четырёх выбранных
квадратов центры не лежат на одной прямой. Докажите, что Витя сможет осуществить свою задумку при любом натуральном
Источники:
Подсказка 1
Сначала попробуем рассмотреть конкретные конструкции, которые нарушают свойства из условия. Сколько различных наборов среди них получается? Что можно сказать про количество пар клеток, лежащих на одной строке или столбце и про количество четвёрок, лежащих на одной прямой?
Подсказка 2
Для оценки количества четвёрок, лежащих на одной прямой, воспользуемся рассуждением о том, что любую прямую можно задать двумя точками. Точки в данном случае выбираем по серединам клеток. Сколько различных наборов из n клеток можно выбрать так, что они не будут соответствовать какому-то из разобранных свойств (то есть не подходить под условие)?
Подсказка 3
Предположим противное, то есть то, что у Вити не получится выбрать ни один набор. Всего наборов, в которых пары клеток не лежат на одной строке/столбце, n! (различные перестановки). Теперь сравним это количество с количеством "плохих" наборов с четвёрками клеток, не удовлетворяющим свойствам. Какой вывод можем сделать?
Подсказка 4
Неравенство от противного не выполняется при достаточно больших n (возможно предоставить точную оценку). Для меньших случаев достаточно рассмотреть частные и показать удовлетворяющие свойствам наборы.
Для начала рассмотрим, сколько различных наборов из клеток можно выбрать, чтобы никакие две не находились в одной строке или
столбце. Всевозможных способов выбрать
клеток так, чтобы в каждой строке и в каждом столбце была ровно одна — ровно число
перестановок
Это можно объяснить тем, что, допустим, выбирая по клетке в строке, с каждой строкой количество
"разрешённых"вариантов уменьшается ровно на 1.
Теперь рассмотрим четвёрки клеток, центры которых лежат на одной прямой. Ясно, что их координаты по оси ординат и абсцисс
образуют арифметическую прогрессию с начальным членом и шагом
для которых выполняется:
Шаг может принимать значения от 1 до можем оценить сверху количество плохих расстановок по строкам и столбцам
(отдельно):
"Запрещённая"четвёрка определяется выбором прогрессии по столбцам, по строкам, направлением (по строкам и столбцам). Каждая
"запрещённая"четвёрка клеток встречается в любом наборе из содержащем эти четыре клетки. Остальные
клетки можно
выбрать произвольно (с учётом строки–столбца), то есть из
вариантов.
Получается, что количество всех "плохих"(содержащих хотя бы одну "запрещённую"четвёрку) наборов не превосходит:
Если бы решений не было, то все вариантов были бы плохими, и мы получили бы неравенство:
Разделим на и упростим:
Но при неравенство не выполняется. Получили противоречие.
Остаётся проверить вручную случаи Примеры правильных построений легко построить, используя вышеуказанные
ограничения и запреты на расположения клеток.
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике отметил точку
— середину стороны
и точку
пересечения высот. Оказалось, что
четырёхугольник
— вписанный. В каком отношении высота
делит сторону
Источники:
Подсказка 1
Хм-м, давайте посмотрим на уголки. Мы знаем некоторые полезные свойства ортоцентра, которые можно использовать в этой задаче. Да-да, мы можем выразить ∠AHB через ∠ACB, а также воспользоваться свойством углов, опирающихся на одну хорду.
Подсказка 2
А теперь внимательно взглянем на △AMC. В нём высота совпадает с медианой, а это значит, что этот треугольник равнобедренный!
Пусть и
— основания высот
и
соответственно.
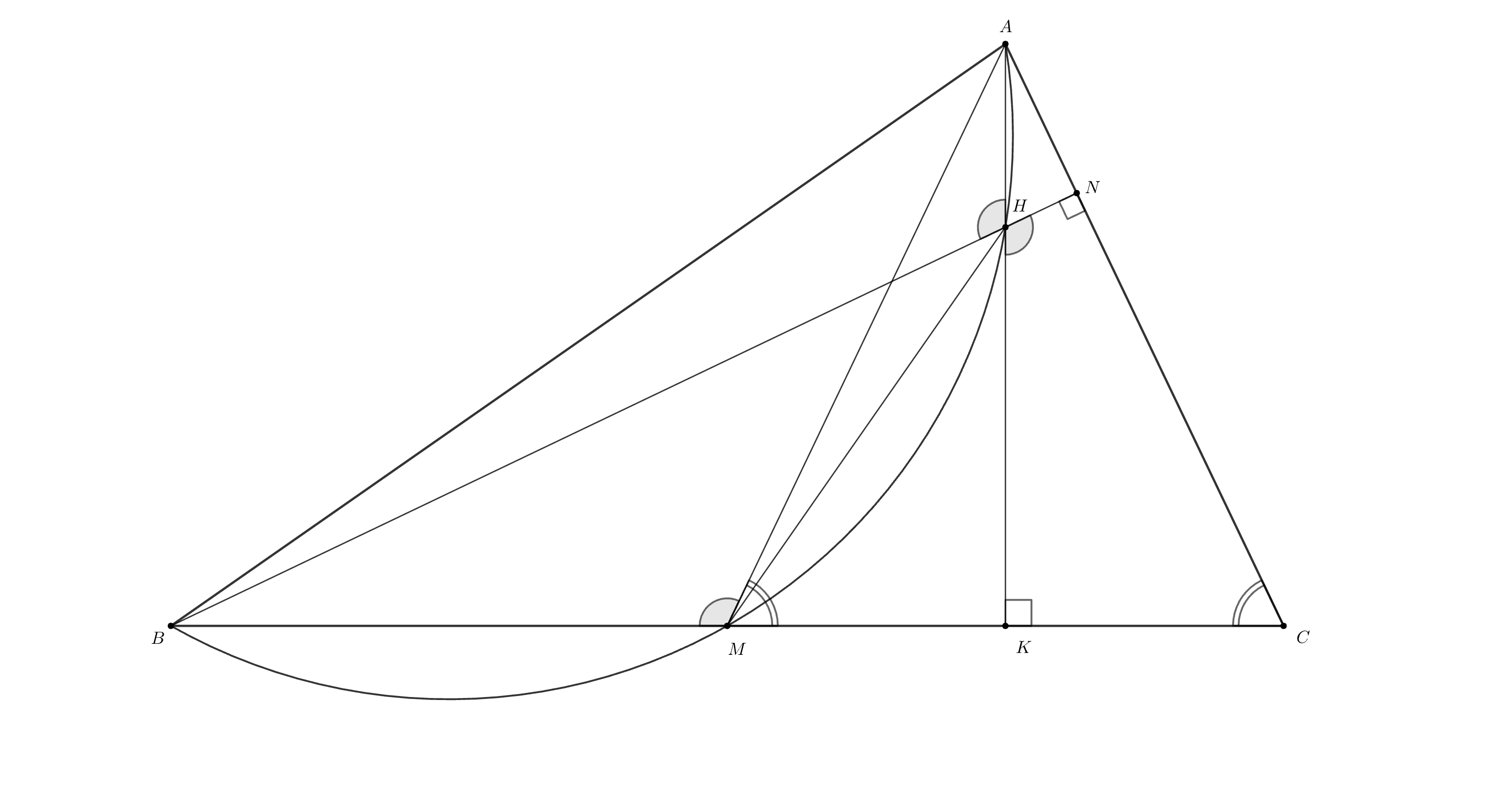
По сумме углов в четырехугольнике
Четырехугольник — вписанный, следовательно,
Кроме того,
Получим, что
Треугольник — равнобедренный,
— высота, следовательно, и медиана. По условию,
— середина
Получим,
что
Ошибка.
Попробуйте повторить позже
Андрей выставил на пустую шахматную доску ферзя и сделал им последовательно несколько ходов (по шахматным правилам),
закрашивая в красный цвет те клетки, через которые прошёл ферзь (включая конечную и начальную). Для каждого хода Андрей
вычислили расстояние между центрами начального и конечного положения ферзя и оказалось, что все эти расстояния различны. Какое
наибольшее количество красных клеток может быть сейчас на доске?
Источники:
Подсказка 1
Вспомните, какие два вида ходов может совершить ферзь?
Подсказка 2
Ага, по прямой и по диагонали. Теперь подумайте, сколько различных расстояний может быть на доске?
Подсказка 3
Если ход ферзя параллелен одной из сторон доски, то его длина может быть целым числом от 1 до 7. Сделайте аналогичный вывод из ходов по диагонали.
Если ход ферзя параллелен одной из сторон доски, то его длина может быть целым числом от 1 до 7. Если параллелен одной из
диагоналей — его длина может принимать значения
Значит, посещенных клеток, включая начальную, будет не
более
Приведем пример посещения ферзем 57 клеток:
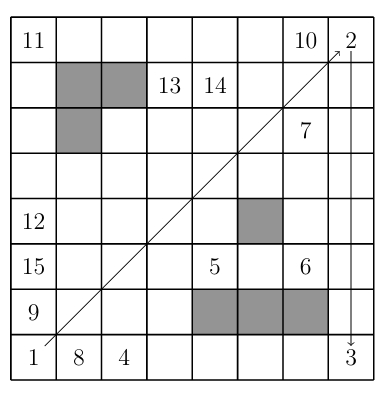
57
Ошибка.
Попробуйте повторить позже
Положительные числа составляют в указанном порядке возрастающую арифметическую прогрессию, причём
Докажите, что
Источники:
Подсказка 1
Для начала распишите равенство через первый член и разность прогрессии.
Подсказка 2
Давайте для удобного преобразования выражения возьмем a за x-3y, а разность прогрессии за 2y.
Подсказка 3
Выразите y через x с помощью данного равенства.
Подсказка 4
Вспомните, что исходные числа у нас положительные.
Подсказка 5
x > 3y, зная это — сделайте оценку на х.
Подсказка 6
Получилось, что x < 3/2, и снова вспомним о том что x > 3y. Завершите оценку на d.
Введем обозначения:
Тогда
Поскольку числа положительные,
Из этого следует, что
Запишем условие задачи в новом виде:
Тогда
Получим, что
Ошибка.
Попробуйте повторить позже
Император планеты Кибертрон приказал создать календарь наподобие земного, то есть разбить год на месяцы так, чтобы один месяц содержал 28 дней, а все остальные — либо 30 , либо 31. Кроме того, он пожелал, чтобы среди любых трёх последовательных месяцев был хотя бы один 31-дневный: «лишние» 31-е дни император планировал сделать всепланетными праздниками, а праздников хотелось побольше. Однако Мудрейший математик Кибертрона установил, что приказ Императора выполнить невозможно. Каким наибольшим числом может быть количество дней в году на планете Кибертрон, если известно, что это число — целое?
Источники:
Подсказка 1
Обозначим за N количество суток в одном году на планете Кибертрон. Подумайте какие условие должны выполняться, чтобы N подходило под условие задачи, а также подумайте сколько может быть месяцев по 30 дней и по 31 дню.
Подсказка 2
Несложным образом можно доказать, что все числа вида 31 * a + 28 приемлемы, подумайте также какие числа ещё могут подойти. Аккуратно разберите все случаи и посмотрите, какие случаи приведут к правильному ответу, а какие нет.
Пусть год на Кибертроне составляет суток. Приказ Императора может быть выполнен тогда и только тогда, когда для некоторых целых
неотрицательных
и
выполняется
Назовём натуральные представимые в указанном виде, приемлемыми, а выражение
— представлением
Найдем
все приемлемые числа
______________________________________________________________________________________________________________________________________________________
Лемма.Пусть число — приемлемо. Тогда можно считать, что в его представлении
где
и такое
(следовательно, и
— единственно.
Доказательство. Пусть но
Тогда
При этом
Следовательно, пара
тоже подходит для представления
Осуществляя данную операцию несколько раз,
найдём требуемое представление. Чтобы показать его единственность, предположим противное, то есть, что для некоторых различных
и
не превосходящих 30
Тогда
Заметим, что левая часть не может быть кратна 31 — противоречие.
_________________________________________________________________________________________________________________________________________________________________________________
Вернемся к задаче. Все числа вида приемлемы
Число вида
приемлемо, только
если
Другими словами, Наибольшее неприемлемое число такого вида —
Аналогично,
(здесь
приемлемо, если
Наибольшее неприемлемое число такого вида — В остальных случаях имеем
где
Тогда
приемлемо тогда и только тогда, когда
Поскольку — целое, получаем, что наибольшее неприемлемое число указанного вида достигается при
в случае нечетного
и
при
в случае нечетного
Значения
будут соответственно равны
Теперь ясно, что наибольшее неприемлемое число возникает при наибольшем значении то есть при
В этом
случае
1393


