Закл 2025
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
На прямоугольном листе бумаги провели несколько отрезков, параллельных его сторонам. Эти отрезки разбили лист на несколько прямоугольников, внутри которых нет проведённых линий. Петя хочет провести в каждом из прямоугольников разбиения одну диагональ, разбив его на два треугольника, и окрасить каждый треугольник либо в чёрный, либо в белый цвет. Верно ли, что он обязательно сможет это сделать так, чтобы никакие два одноцветных треугольника не имели общего отрезка границы?
Источники:
Подсказка 1:
Попробуйте придумать пример такого разделения и раскраски.
Подсказка 2:
Самое простое, что приходит на ум — провести во всех прямоугольниках одинаковую диагональ, например из левого нижнего угла в правой верхний. Можно ли в этом случае как-то раскрасить так, чтобы соблюдалось условие?
Подсказка 3:
С точки зрения раскраски на ум тоже должно прийти самое простое — раскрасить все квадраты некоторым одинаковым образом. Попробуйте обосновать, почему такая раскраска может подойти.
Пусть Петя проведёт в каждом из прямоугольников диагональ из левого нижнего угла в правый верхний. После этого все треугольники, примыкающие к левым верхним углам прямоугольников, он покрасит в чёрный цвет, а остальные — в белый.
Докажем, что такая раскраска подойдёт. Рассмотрим общий отрезок границы двух треугольников. Если этот отрезок диагональный, то сверху к нему примыкает чёрный треугольник, а снизу белый. Если отрезок горизонтальный, то к нему сверху примыкает белый треугольник, а снизу — чёрный; случай вертикального отрезка аналогичен. Поэтому такая раскраска подходит.
да, верно
Ошибка.
Попробуйте повторить позже
Диагонали выпуклого четырёхугольника пересекаются в точке
Точки касания описанных окружностей треугольников
и
с их общими внешними касательными лежат на окружности
Точки касания описанных окружностей треугольников
и
с их общими внешними касательными лежат на окружности
Докажите, что центры окружностей
и
совпадают.
Источники:
Подсказка 1:
Давайте введём следующие обозначения: O_{AB}, O_{BC}, O_{CD}, O_{AD} — центры окружностей (ABE), (BCE), (CDE), (ADE), a T₁, T₂ — точки касания одной из внешних касательных к окружностям, описанным около ABE и CDE. Обратите внимание на прямоугольную трапецию O_{AB}T₁T₂O_{CD}. В частности, на середину O_{AB}O_{CD}. Что можно про неё сказать?
Подсказка 2:
Если сделать симметрию относительно точки O, во что перейдет окружность ω? Какие выводы можно сделать?
Подсказка 3:
Точка O — центр ω. Аналогичные рассуждения можно проделать с серединой O_{AD}O_{BC}. Значит, мы хотим показать, что середины отрезков O_{AD}O_{BC} и O_{AB}O_{CD} совпадают. А что для этого достаточно доказать?
Подсказка 4:
Достаточно доказать, что четырехугольник O_{AB}O_{BC}O_{CD}O_{AD} — параллелограмм. Попробуйте для этого показать, что его противолежащие стороны параллельны.
Обозначим центры описанных окружностей треугольников
через
соответственно. Пусть
— точки касания одной из общих касательных с описанными окружностями треугольников
и
соответственно; обозначим через
и
середины отрезков
и
соответственно. Тогда в прямоугольной
трапеции
прямая
— средняя линия, поэтому она является серединным перпендикуляром к отрезку
Заметим,
что окружность
симметрична относительно прямой
на которой также лежит точка
значит,
— центр
![]()
Аналогично получаем, что середина отрезка является центром
Поэтому утверждение задачи равносильно тому, что
— параллелограмм. Для доказательства этого достаточно заметить, что
и
— серединные
перпендикуляры к отрезкам
и
поэтому
аналогично,
откуда и следует
требуемое.
![]()
Ошибка.
Попробуйте повторить позже
Найдите все натуральные для которых существует такое чётное натуральное
что число
является точным квадратом.
Источники:
Подсказка 1:
Попробуйте сначала вручную разобраться с n = 1, 2, 3. Для этих случаев достаточно вспомнить утверждение о том, что если произведение двух взаимно простых чисел — квадрат, то каждое из них также является квадратом. В частности, при n = 3 надо поработать с нодами скобок a - 1, a + 1, a² + a + 1. Быть может, этот ход мыслей можно развить и для больших n?
Подсказка 2:
Итак, скорее всего вы поняли, что n = 1, 2 подойдёт, а n = 3 — нет. Чем остальные случаи отличаются. Например, если n > 3, то оно находится между двумя натуральными степенями двойки. То есть существует такое натуральное k, что 2^k ≤ n < 2^{k + 1}. Подумайте, как это можно использовать.
Подсказка 3:
Если записать скобку a^{2^k} – 1 как (a^{2^{k – 1}} – 1)(a^{2^{k – 1}} + 1), то становится ясно, что все произведение состоит из скобки a^{2^{k – 1}} + 1 и скобок вида a^m – 1. А как насчёт того, чтобы посмотреть на нод выражений a^{2^{k – 1}} + 1 и a^{2^k} – 1 с произвольной скобкой a^m – 1?
Подсказка 4:
Нод второго выражения и a^m – 1 кратен ноду первого выражения и a^m - 1. Чтобы было проще работать, вот вам интересный факт: нод второй скобки и a^m – 1 равен a^нод(2^k, m) – 1. Осталось поработать с нодом 2^k и m.
Подсказка 5:
Исходя из выбора k, ясно, что нод 2^k и m не превышает 2^{k – 1}. Попробуйте теперь показать, что ноды выражений a^{2^{k – 1}} + 1 и a^{2^k} – 1 с a^m – 1 совпадают. Кажется, это раскроет идею подсказки 3.
Подсказка 6:
Стало быть, a^{2^{k – 1}} + 1 — точный квадрат. А вас это не смущает?
Заметим, что для подойдёт
Для
подойдёт
Предположим, что для нашлось требуемое число
Тогда число
является точным квадратом. Поскольку
числа и
взаимно просты. Раз число
нечётно, числа
и
также взаимно просты. Следовательно,
числа
и
— точные квадраты. В частности, число
при делении на 3 может давать лишь остаток 0 или 1, а
тогда число
не делится на 3. Отсюда
значит, числа и
также являются точными квадратами. Но второе являться квадратом не может,
поскольку
Противоречие.
Осталось доказать, что требуемого не существует при
Предположим, что такое
нашлось. Возьмём такое натуральное
что
Поскольку
число
представляется в виде произведения и нескольких множителей вида
где
и
Докажем, что множитель взаимно прост со всеми остальными множителями в этом разложении. Пусть
и
имеют некоторый общий делитель
Тогда и НОД
и
кратен
Но
Поскольку и
число
не может делиться на
Таким образом,
— степень двойки,
не превосходящая
Следовательно,
делится на НОД
и
а, значит, делится и на
Поскольку
чётно, числа
и
не имеют общих делителей, отличных от 1, значит,
что и
требовалось.
Множитель взаимно прост со всеми остальными множителями в произведении, являющемся точным квадратом, поэтому он
сам является точным квадратом. Тогда
и
— отличающиеся на 1 квадраты натуральных чисел, что невозможно. Значит,
наше предположение неверно, и для
требуемых чисел
не найдётся.
и
Ошибка.
Попробуйте повторить позже
Шахматного короля поставили на клетку доски 8 × 8 и сделали им 64 хода так, что он побывал на всех клетках и вернулся в исходную клетку. В каждый момент времени вычислялось расстояние от центра клетки, в которой находился король, до центра всей доски. Назовём сделанный ход приятным, если в результате хода это расстояние стало меньше, чем было до хода. Найдите наибольшее возможное количество приятных ходов. (Шахматный король за один ход передвигается на клетку, соседнюю по стороне или по углу.)
Источники:
Подсказка 1:
Чтобы было удобно делать оценку, нужно понять, сколько имеется различных значений расстояний от центра и сколько клеток соответствуют каждому значению.
Подсказка 2:
Давайте клеткам, соответствующим самому маленькому значению, сопоставим 1, клеткам, соответствующим следующему значению — 2 и так далее. Как, используя эту нумерацию, сделать оценку?
Подсказка 3:
Смотрите, например, ход из клетки с номером 2 будет приятным лишь в том случае, если он сделан в клетку с номером 1. Но клеток с номером 2 — 8, а с номером 1 — 4, значит, как минимум, 4 хода из клеток с номером 2 будут неприятными. Попробуйте развить эту мысль на другие клетки.
Подсказка 4:
Если рассмотреть переходы из клеток с номером 1 и 2 в клетки с номерами, не меньшими 6, должна получиться оценка в 44 приятных хода. Не забудьте придумать пример.
Докажем, что среди ходов должно быть хотя бы 20 неприятных (а значит, количество приятных ходов не больше 44). Расставим в клетках числа, как показано на первом рисунке; клетки с одинаковыми числами удалены на одно и то же расстояние от центра, а клетки с меньшими номерами ближе к центру, чем клетки с большими.
![]()
Каждый ход из клетки с числом 1 не уменьшает расстояния до центра и потому неприятен — таких ходов 4. Ход из клетки с числом 2 может быть приятным, только когда он идёт в клетку с числом 1. Но на доске восемь чисел 2 и только четыре числа 1, поэтому хотя бы четыре хода из клеток с числом 2 будут неприятными.
Рассмотрим теперь ходы, ведущие в 32 клетки с числами, не меньшими 6. Заметим, что эти ходы не могут идти из клеток с числами 1 и
2, то есть в рассуждении выше они не учтены. Такой ход может быть приятным, только если он идёт из клетки с номером, не меньшим 7;
однако таких клеток всего 20. Значит, среди рассмотренных ходов ещё неприятных, и общее количество неприятных ходов не
меньше, чем
Пример обхода, в котором 44 приятных хода (синие), приведён на втором рисунке (начинаем движение королём с левой нижней клетки вверх).
![]()
Замечание. По сути, в последней части доказательства оценки показано, что среди ходов, ведущих в клетки, отмеченные зелёным на первом рисунке, есть не менее трёх неприятных. Это можно доказать разными способами, например, проведя небольшой перебор.
44 хода
Ошибка.
Попробуйте повторить позже
Пусть и
— приведённые квадратные трёхчлены, а точки
и
— соответственно вершины парабол
и
Через
будем обозначать наименьшее значение функции
Известно, что разности
оказались равными положительными числами. Найдите угол между прямой и прямой, содержащей ось
Источники:
Обозначим данные трёхчлены:
где и
— координаты вершин парабол. Тогда
а
Если то минимальное значение выражения
равняется нулю, откуда
Последнее противоречит тому, что
— положительное число. Таким образом, откуда
Аналогично, и
Теперь условие равенства разностей переписывается в виде Отсюда, поскольку
и
получаем
то есть
Значит, искомый угол равен
Ошибка.
Попробуйте повторить позже
Петя выбрал 100 попарно различных положительных чисел, меньших 1, и расставил их по кругу. Затем он проделывает с ними операции. За
одну операцию можно взять три стоящих подряд (именно в таком порядке) числа и заменить число
на
. При каком
наибольшем
Петя мог выбрать исходные числа и сделать несколько операций так, чтобы после них среди чисел оказалось
целых?
Источники:
Оценка. Покажем, что целых чисел никогда не станет больше 50. Будем следить за разностями между числом и следующим за ним по
часовой стрелке. Если подряд стояли числа
то их разности были равны
и
После применения операции к числу
получаются числа
и
разности которых равны
Итак, в результате операции две соседние разности просто переставляются местами. Изначально все разности были нецелыми, поэтому они в любой момент времени будут нецелыми. Таким образом, два целых числа никогда не могут появиться рядом и, значит, их будет не больше 50.
Пример. Для начала расставим по кругу попеременно числа
и
Если с каждым числом
проделать операцию, то оно
будет заменено на
и числа через одно будут целыми. Осталось подправить пример так, чтобы все числа стали
различными. Для этого достаточно прибавить к каждому числу
по своему маленькому числу, а к каждому числу
— сумму чисел,
прибавленных к его соседям. Например, выбрав
можно прибавить к последовательным числам
числа
тогда к числам
будут прибавляться числа
В результате все числа станут
различными.
при
Ошибка.
Попробуйте повторить позже
В строку выписаны числа 1, 2, 3, …, 60 (ровно в таком порядке). Игорь и Руслан по очереди ставят знаки и
между ними,
начинает Игорь; за ход каждый ставит один знак. Когда между каждыми двумя соседними числами поставлен знак, вычисляется значение
полученного выражения. Если оно делится на 3, то победа присуждается Игорю, иначе Руслану. Кто из игроков может выиграть,
независимо от действий соперника?
Источники:
Подсказка 1:
Ясно, что в контексте задачи все числа для удобства можно заменить на остатки при делении на 3. Попробуйте придумать какую-то простую стратегию за Игоря, основанную на симметрии, чтобы все слагаемые взаимно уничтожились.
Подсказка 2:
Значит, Игорь должен сделать так, чтобы для любого слагаемого со знаком + нашлось слагаемое, равное по модулю, но со знаком минус.
Подсказка 3:
Всего имеется 59 мест, в которые нужно поставить знаки. Как насчёт того, чтобы Игорь первым ходом поставил некоторый знак в центральный, а потом как-то отвечал на ходы Руслана в другую половину?
Заменим все числа в строке на их остатки от деления на 3, от этого результат игры не изменится. Получим строку
…,
Промежутки между числами пронумеруем слева направо от 1 до 59. Первым ходом Игорь ставит
знак минус в 30-й промежуток, а все остальные промежутки он разбивает на пары вида
Если Руслан ставит в
какой-то промежуток знак плюс или минус, то Игорь в парный промежуток ставит минус или плюс соответственно. А если
Руслан ставит знак умножить, то Игорь ставит в парный промежуток также знак умножить. Когда все знаки расставлены,
полученное выражение разбивается на несколько слагаемых. При этом в левой и правой половинах выражения набор слагаемых
одинаковый, но берутся они с противоположными знаками. Следовательно, его значение будет давать остаток 0 при делении на
3.
Игорь
Ошибка.
Попробуйте повторить позже
На периметре треугольника выбраны точки
так, что при обходе периметра точки встречаются в
порядке
Оказалось, что
Докажите, что периметры треугольников, образованных тройками прямых
и
равны.
Источники:
Начнём со следующей полезной леммы.
Лемма. Пусть точки и
выбраны соответственно на сторонах
и
параллелограмма
так, что
Тогда точка
равноудалена от прямых
и
Доказательство. Поскольку и
имеем
Так как
отсюда и следует, что
расстояния от точки
до прямых
и
равны.
.png)
_________________________________________________________________________________________________________________________________________________________________________________
Перейдём к решению. Пусть прямые из условия образуют треугольники и
(точки обозначены как на рис.). Выберем
точку
так, что
— параллелограмм; согласно лемме, точка
равноудалена от прямых
и
; значит,
существует окружность с центром
касающаяся этих прямых в некоторых точках
и
соответственно. Тогда из равенств
отрезков касательных вытекает, что
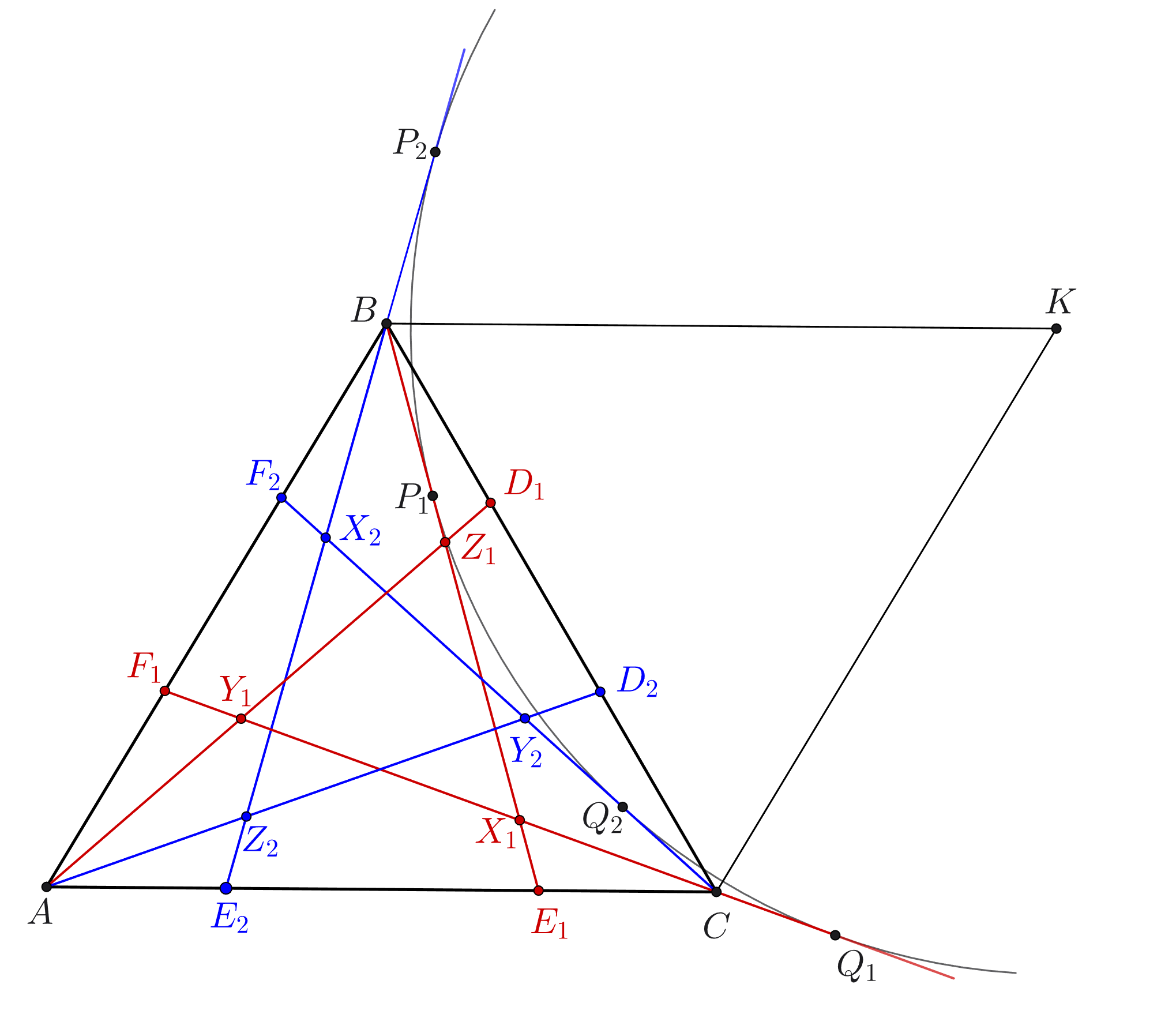
Аналогично получаем, что и
Складывая полученные три равенства, получаем
требуемое равенство периметров.


