Регион 2016
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Петя выбрал несколько последовательных натуральных чисел и каждое записал либо красным, либо синим карандашом (оба цвета присутствуют). Может ли сумма наименьшего общего кратного всех красных чисел и наименьшего общего кратного всех синих чисел являться степенью двойки?
Источники:
Подсказка 1
Попробуем идти от противного. Выберем максимальную степень двойки, которую можно найти среди выписанных натуральных чисел. Могут ли быть выписаны две таких?
Подсказка 2
Верно, не могут! Ведь тогда одна из этих степеней больше максимальной. А что тогда можно сказать о наименьшем общем кратном той группы, в которой эта степень двойки не содержится?
Рассмотрим степени двойки, на которые делятся выписанные числа; пусть — наибольшая из них. Если хотя бы два выписанных числа
делятся на
то два соседних таких числа будут различаться на
Значит, одно из них делится на
что невозможно в силу
выбора
Следовательно, среди выписанных чисел ровно одно делится на
Наименьшее общее кратное группы, содержащей это число, будет делиться на а НОК оставшейся группы — не будет. Значит, сумма
этих НОК не делится на
с другой стороны, эта сумма больше чем
Поэтому эта сумма не может быть степенью
двойки.
Нет
Ошибка.
Попробуйте повторить позже
Дан равнобедренный треугольник В окружности
описанной около треугольника
проведен диаметр
Прямая, проходящая через точку
параллельно
пересекает отрезки
и
в точках
и
соответственно. Докажите, что
— середина отрезка
Источники:
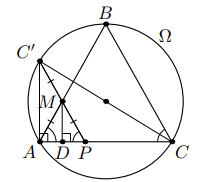
Так как диаметр
имеем
Поскольку
получаем
Значит, треугольник
— равнобедренный, и поэтому его высота
является и медианой. Так как
и
по теореме Фалеса получаем,
что
Ошибка.
Попробуйте повторить позже
Назовём непустое (конечное или бесконечное) множество состоящее из натуральных чисел, полным, если для любых натуральных
и
(не обязательно различных и не обязательно лежащих в
при которых
лежит в
число
также лежит в
Найдите все
полные множества натуральных чисел.
Подсказка 1
Из условия о том, что если a+b содержится в A, то и ab содержится в A можно сделать следующий вывод: если n содержится в A, то и 1*(n-1) содержится в A. Отсюда сразу следует вид возможных множеств, если они конечны.
Подсказка 2
Действительно, у конечного A есть максимальный элемент m, соответственно есть и все числа от 1 до него. Осталось понять, что при достаточно большом m, число 2*(m-2) окажется больше него, а это противоречит максимальности m. Теперь разберёмся с бесконечными множествами, в них для любого числа найдётся больший его элемент A. Может ли какое-то число не присутствовать в A?
Подсказка 3
По ранее доказанному любое натуральное число меньше какого-то элемента A, а значит является элементом A. Таким образом A — множество натуральных чисел.
Пусть в множестве есть число
тогда поскольку
в множестве
есть и
Тогда если конечно и в нём имеется максимальный элемент
то в нём имеются все числа от
до
Притом если
то
что противоречит максимальности элемента
Нетрудно убедиться, что при
от
до
множества вида {1, 2, …n}
являются решениями.
Если же бесконечно, при отсутствии в нём натурального
в нём по доказанному отсутствуют все числа большие
что
противоречит бесконечности. Значит
— множество натуральных чисел.
а также
Ошибка.
Попробуйте повторить позже
В треугольнике проведена биссектриса
На отрезке
выбрана точка
Касательная в точке
к окружности
описанной около треугольника
пересекает луч
в точке
Касательные в точках
и
к окружности
описанной около
треугольника
пересекаются в точке
Докажите, что прямые
и
параллельны.
Так как прямая касается описанной окружность треугольника
можно написать следующую цепочку равенств:
Поэтому треугольник — равнобедренный.
![]()
Заметим, что угол равен углу
в силу касания описанной окружности треугольника
и прямой
Следовательно,
равнобедренные треугольники
и
подобны, а значит,
Получаем, что четырёхугольник
вписанный, поэтому углы
и
равны, но угол
равен углу
откуда и следует искомая
параллельность.

