Квадратичная функция (страница 2)
Готовиться с нами - ЛЕГКО!

На рисунке изображен график функции \(y=ax^2+bx+c\).

Каковы знаки коэффициентов \(a\) и \(c\)?
1) \(a<0, c>0\qquad \) 2) \(a<0, c<0\qquad \) 3) \(a>0, c<0\qquad \) 4) \(a>0, c>0\)
Так как ветви параболы направлены вниз, то \(a<0\). Следовательно, либо 1, либо 2. Коэффициент \(c\) отвечает за ординату точки пересечения параболы с осью \(Oy\) (то есть любая парабола вида \(y=ax^2+bx+c\) проходит через точку \(A(0;c)\)). (Действительно, если подставить в \(y=ax^2+bx+c\) вместо \(x=0\), то получим \(y=0+0+c=c\).)
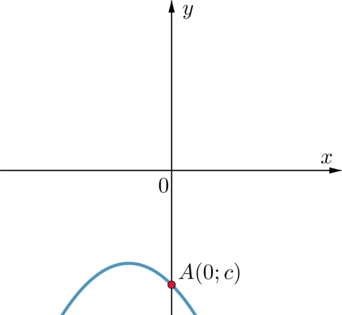
Из рисунка видно, что парабола пересекает ось \(Oy\) на отрицательной части, то есть \(c<0\). Значит, ответ 2.
Дана функция \(y=ax^2+bx+c\). На каком из рисунков изображен график этой функции, если известно, что \(a>0, c>0\)?
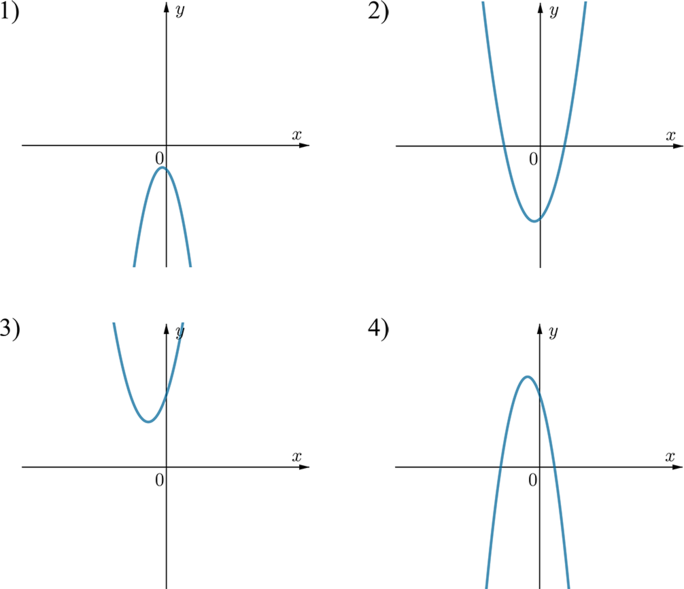
Так как \(a>0\), то ветви параболы направлены вверх. Следовательно, либо 2, либо 3. Коэффициент \(c\) отвечает за ординату точки пересечения параболы с осью \(Oy\) (то есть любая парабола вида \(y=ax^2+bx+c\) проходит через точку \(A(0;c)\)). (Действительно, если подставить в \(y=ax^2+bx+c\) вместо \(x=0\), то получим \(y=0+0+c=c\).)
Так как \(c>0\), то парабола должна пересекать \(Oy\) на положительной части. Следовательно, это парабола 3.
На рисунке изображены графики функций вида \(y=ax^2+bx+c\). Установите соответствие между графиками и знаками коэффициентов \(a, c\).
ГРАФИКИ:

КОЭФФИЦИЕНТЫ:
1) \(a>0, c>0\qquad \) 2) \(a>0, c<0\qquad \) 3) \(a<0, c<0\)
В таблице под каждой буквой укажите соответствующий номер.
Ответ: \(\begin{array}{|c|c|c|} \hline \text{А} & \text{Б} & \text{В} \\ \hline && \\ \hline \end{array}\)
Если ветви параболы направлены вверх, то \(a>0\), вниз – то \(a<0\). У параболы А ветви направлены вниз, следовательно, А – 3.
Коэффициент \(c\) отвечает за ординату точки пересечения параболы с осью \(Oy\) (то есть любая парабола вида \(y=ax^2+bx+c\) проходит через точку \(A(0;c)\)). (Действительно, если подставить в \(y=ax^2+bx+c\) вместо \(x=0\), то получим \(y=0+0+c=c\).)
Парабола Б пересекает ось \(Oy\) на положительной части, то есть \(c>0\). Следовательно, Б – 1. Тогда В – 2.
Ответ: \(\begin{array}{|c|c|c|} \hline \text{А} & \text{Б} & \text{В} \\ \hline 3&1&2 \\ \hline \end{array}\)
В ответ запишем 312.
Найдите значение \(c\) по графику функции \(y=ax^2+bx+c\), изображенному на рисунке.
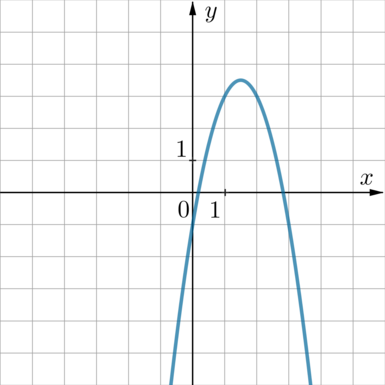
Коэффициент \(c\) отвечает за ординату точки пересечения параболы с осью \(Oy\) (то есть любая парабола вида \(y=ax^2+bx+c\) проходит через точку \(A(0;c)\)). (Действительно, если подставить в \(y=ax^2+bx+c\) вместо \(x=0\), то получим \(y=0+0+c=c\).)
Данная парабола пересекает ось \(Oy\) в точке \(y=-1\). Следовательно, \(c=-1\).
Найдите знак \(ab\) по графику функции \(y=ax^2+bx+c\), изображенному на рисунке.

В ответе укажите \(1\), если \(ab>0\), и \(-1\), если \(ab<0\).
Абсцисса вершины параболы \(y=ax^2+bx+c\) ищется по формуле \(x_0=\dfrac{-b}{2a}\). Следовательно, если \(x_0>0\), то \(\frac ba<0\), и наоборот. На нашем рисунке у параболы \(x_0>0\), следовательно, \(\frac ba<0\), откуда также следует, что и \(ab<0\). Тогда ответ \(-1\).
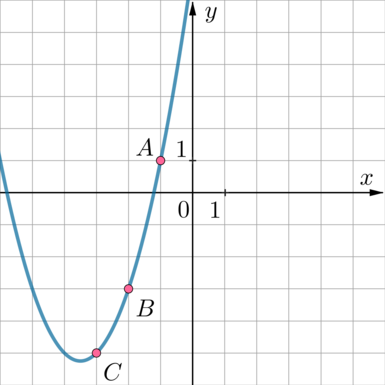
Найдите значение \(a\) по графику функции \(y=ax^2+bx+c\), изображенному на рисунке.
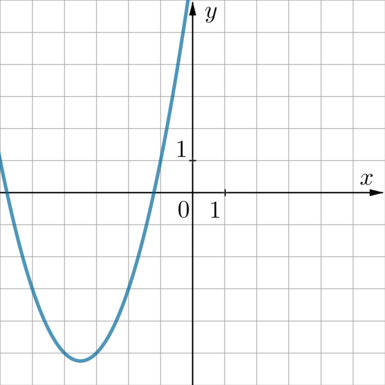
Заметим, что парабола проходит через точки: \(A(-1;1)\), \(B(-2;-3)\), \(C(-3; -5)\).
Следовательно, можно составить систему: \[\begin{cases}
1=a-b+c\\
-3=4a-2b+c\\
-5=9a-3b+c \end{cases}\] Вычтем из второго уравнения первое, из третьего первое и получим новую систему: \[\begin{cases}
-4=3a-b\\
-6=8a-2b \end{cases} \quad\Rightarrow\quad \begin{cases}
8=-6a+2b\\
-6=8a-2b \end{cases}\] Сложим два полученных уравнения, тогда \(2=2a\), откуда \(a=1\).
Найдите значение \(a\) по графику функции \(y=ax^2+bx+c\), изображенному на рисунке.
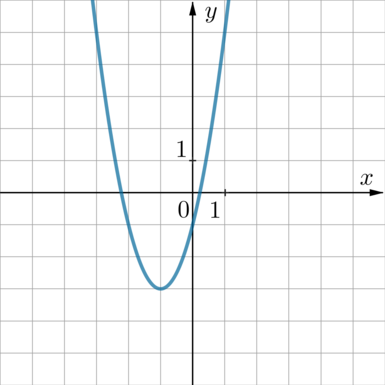
Из рисунка видно, что абсцисса вершины параболы равна \(x_0=-1\). Следовательно, \(-\frac b{2a}=-1\), откуда \(b=2a\) (*).
Ордината вершины параболы равна \(y_0=-3\), следовательно, \(-3=a\cdot
(-1)^2+b\cdot (-1)+c\), откуда \(-3=a-b+c\) (**).
Так как парабола пересекает ось \(Oy\) в точке \(y=-1\), то есть проходит через точку \((0;-1)\), то \(-1=a\cdot 0^2+b\cdot 0+c\), откуда \(c=-1\).
(Коэффициент \(c\) отвечает за ординату точки пересечения параболы с осью \(Oy\) (то есть любая парабола вида \(y=ax^2+bx+c\) проходит через точку \(A(0;c)\)). Действительно, если подставить в \(y=ax^2+bx+c\) вместо \(x=0\), то получим \(y=0+0+c=c\).)
Подставляя в (**) \(c=-1\), получим \(-3=a-b-1\). Отсюда выразим \(a=b-2\) и подставим в \(b=2a\): \(b=2b-4\), откуда \(b=4\), \(a=2\).



