Прямоугольник и квадрат
Готовиться с нами - ЛЕГКО!

Расстояние от точки пересечения диагоналей прямоугольника до прямой, содержащей его большую сторону, равно \(2,5\). Найдите меньшую сторону прямоугольника.
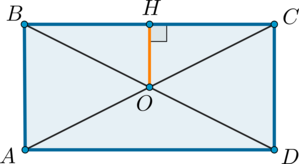
Рассмотрим прямоугольник \(ABCD\). Пусть \(O\) – точка пересечения диагоналей, \(OH=2,5\) – расстояние от точки \(O\) до большей стороны.
Т.к. диагонали прямоугольника равны и точкой пересечения делятся пополам, то \(BO=CO\). Следовательно, \(\triangle BOH=\triangle COH\) как прямоугольные по катету и гипотенузе. Следовательно, \(BH=CH\). Таким образом, \(OH\) – средняя линия в \(\triangle ABC\), следовательно, она равна половине \(AB\). Значит, \(AB=2\cdot 2,5=5\).
В прямоугольнике \(ABCD\) диагональ \(AC = 2\cdot CD\). Найдите разность \(\angle BAC - \angle CAD\). Ответ дайте в градусах.

Треугольник \(ACD\) – прямоугольный, причём в нём катет равен половине гипотенузы, значит этот катет лежит против угла в \(30^{\circ}\), то есть \(\angle CAD = 30^{\circ}\).
\(\angle BAC = 90^{\circ} - \angle CAD = 60^{\circ}\), тогда \(\angle BAC - \angle CAD = 60^{\circ} - 30^{\circ} = 30^{\circ}\).
\(O\) – точка пересечения диагоналей прямоугольника \(ABCD\), \(\angle OAD = 28^{\circ}\). Найдите \(\angle AOD\). Ответ дайте в градусах.
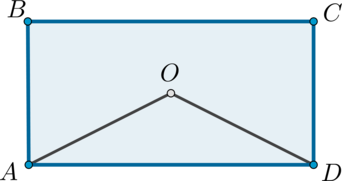
В прямоугольнике диагонали пересекаются, точкой пересечения делятся пополам и равны, тогда \(AO = OD\), следовательно, \(\angle ADO = \angle OAD = 28^{\circ}\), тогда \(\angle AOD = 180^{\circ} - 2\cdot 28^{\circ} = 124^{\circ}\).


