Площади и углы трапеции
Готовиться с нами - ЛЕГКО!

В трапеции \(ABCD\) с основаниями \(AD\) и \(BC\) проведены биссектрисы углов \(A\) и \(B\), пересекающие основания соответственно в точках \(N\) и \(K\). Найдите периметр четырехугольника \(ABNK\), если \(AB=5\).
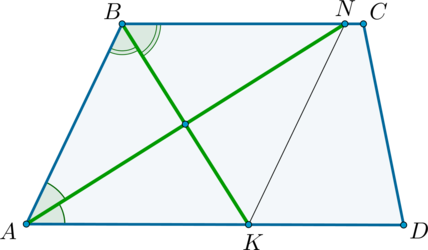
\(\angle AKB=\angle KBN\) как накрест лежащие при \(AD\parallel BC\) и \(BK\) секущей. Следовательно, \(\angle AKB=\angle ABK\), следовательно, \(\triangle BAK\) равнобедренный. Отсюда \(AB=AK=5\).
Аналогично, \(\angle BNA=\angle NAK=\angle NAB\), следовательно, \(\triangle ABN\) – равнобедренный. Отсюда \(AB=BN=5\).
Заметим, что \(AK=BN=5\) и \(AK\parallel BN\), следовательно, по признаку \(ABNK\) – параллелограмм. Следовательно, \(NK=AB=5\). Следовательно, периметр \(ABNK\) равен \(5+5+5+5=20\).
Одно из оснований трапеции в \(5\) раз меньше ее средней линии. Во сколько раз оно меньше другого основания трапеции?
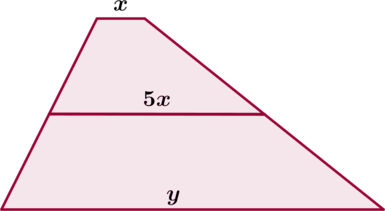
Обозначим меньшее основание трапеции за \(x\), большее – за \(y\). Тогда \(5x\) – длина средней линии трапеции. Так как средняя линия равна полусумме оснований, то \[x+y=2\cdot 5x\quad\Leftrightarrow\quad y=9x.\] Следовательно, меньшее основание в 9 раз меньше большего.
В равнобедренной трапеции высота равна \(5\), а диагонали взаимно перпендикулярны. Найдите среднюю линию этой трапеции.
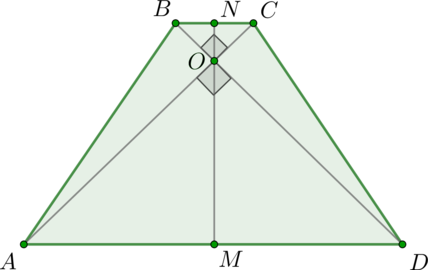
Рассмотрим трапецию \(ABCD\), показанную на рисунке. Проведем \(NM\) – отрезок, соединяющий середины оснований. Так как середины оснований трапеции и точка пересечения диагоналей лежат на одной прямой, то \(O\in MN\).
Так как трапеция равнобедренная, то \(AO=OD\), следовательно, \(\triangle AOD\) равнобедренный, значит, \(OM\) не только медиана, но и высота. Следовательно, \(NM\) – высота трапеции.
Так как \(\triangle AOD\) и \(\triangle BOC\) прямоугольные, то медианы, проведенные из их прямых углов, равны половине их гипотенуз, то есть \(OM=0,5AD\) и \(ON=0,5BC\). Следовательно, \(MN=0,5(AD+BC)\). Так как средняя линия \(l\) трапеции равна полусумме оснований, то \(l=MN=5\).
Основания трапеции равны \(3\) и \(2\). Найдите отрезок, соединяющий середины диагоналей трапеции.
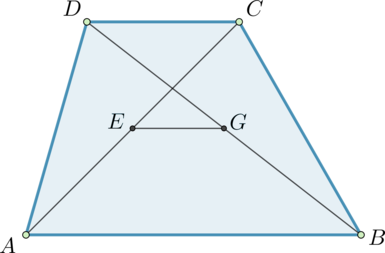
Пусть \(M\) и \(N\) – середины боковых сторон трапеции. Отрезок \(MN\) пересекает диагонали в серединах: \(E\) и \(G\).
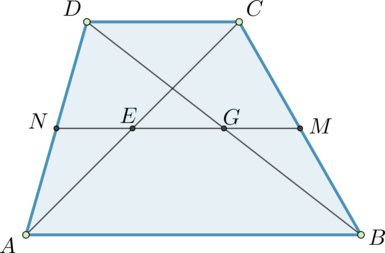
Действительно, так как \(MN\) – средняя линия, то \(MN\parallel AB\parallel CD\). Следовательно, если рассмотреть \(\triangle ADC\), то \(NE\parallel CD\). Так как к тому же \(N\) – середина \(AD\), то по теореме Фалеса \(E\) – середина \(AC\). Аналогично доказывается, что \(G\) – середина \(DB\).
Так как средняя линия равна полусумме оснований, то \(MN=0,5(3+2)=2,5\). Так как \(NE\) и \(GM\) – средние линии в треугольниках \(ADC\) и \(BDC\) соответственно, параллельные \(CD\), то \(NE=GM=0,5CD=0,5\cdot 2=1\). Следовательно, \(EG=MN-NE-GM=2,5-1-1=0,5\).
В равнобедренной трапеции большее основание равно \(25\), боковая сторона равна \(10\), угол между ними \(60^\circ\). Найдите меньшее основание.

\(\angle A=60^\circ\). Проведем высоту \(BH\).

По свойству равнобедренной трапеции \(AH=(AD-BC):2\). В прямоугольном \(\triangle ABH\) \(\angle ABH=90^\circ-60^\circ=30^\circ\). Катет, лежащий против угла \(30^\circ\), равен половине гипотенузы: \(AH=AB:2=5\). Следовательно, \[5=(25-BC):2\quad\Rightarrow\quad BC=15\]
В равнобедренной трапеции основания равны \(12\) и \(27\), острый угол равен \(60^\circ\). Найдите ее периметр.

\(\angle A=60^\circ\). Проведем высоту \(BH\).

По свойству равнобедренной трапеции \(AH=(AD-BC):2=(27-12):2=7,5\). В прямоугольном \(\triangle ABH\) \(\angle
ABH=90^\circ-60^\circ=30^\circ\). Катет, лежащий против угла \(30^\circ\), равен половине гипотенузы: \(AH=AB:2\). Значит, \(AB=2AH=15\). Следовательно, периметр равен \[P=15+15+12+27=69\]
Основания равнобедренной трапеции равны \(15\) и \(9\), один из углов равен \(45^\circ\). Найдите высоту трапеции.

\(\angle A=45^\circ\). Проведем высоту \(BH\).
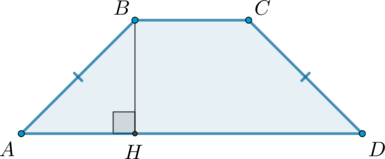
По свойству равнобедренной трапеции \(AH=(AD-BC):2=(15-9):2=3\). В прямоугольном \(\triangle ABH\) \(\angle
ABH=90^\circ-45^\circ=45^\circ\). Следовательно, \(\triangle ABH\) равнобедренный и \(BH=AH=3\).



